Filtre de Butterworth

Filtre de Butterworth
Page d'aide sur l'homonymie Pour les articles homonymes, voir Butterworth.
Diagramme de Bode d'un filtre de Butterworth passe-bas du premier ordre

Un filtre de Butterworth est un type de modèle de filtre linéaire, conçu pour posséder un gain aussi constant que possible dans sa bande passante.

Les filtres de Butterworth furent décrits pour la première fois par l'ingénieur britannique Stephen Butterworth [1].

Sommaire

Caractéristiques

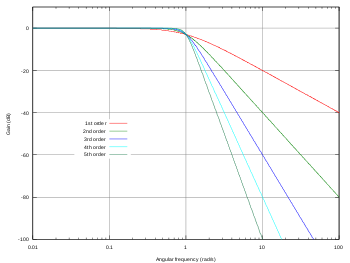
Gains de filtres de Butterworth passe-bas d'ordre 1 à 5 en fonction de la fréquence

Le gain d'un filtre de Butterworth est le plus constant possible dans la bande passante et tend vers 0 dans la bande de coupure. Sur un diagramme de Bode logarithmique, cette réponse décroît linéairement vers -∞, de -6 dB/octave (-20db/décade) pour un filtre de premier ordre, -12db/octave soit -40dB/decade pour un filtre de second ordre, -18dB/octave soit -60dB/decade pour un filtre de troisième ordre, etc.


Fonction de transfert

Comme pour tous les filtres linéaires, le prototype étudié est le filtre passe-bas, qui peut être facilement modifié en filtre passe-haut ou placé en série pour former des filtres passe-bande ou coupe-bande.

Le gain d'un filtre de Butterworth passe-bas d'ordre n est :

G_n(\omega) = \left | H_n(j \omega) \right | = {1 \over \sqrt{ 1 + (\omega / \omega_\mathrm{c}) ^ {2 n}} }

où Gn est le gain du filtre,

Hn sa fonction de transfert,
j l'unité imaginaire : j2 = − 1 (les électroniciens utilisent la lettre j au lieu de i pour ne pas confondre avec i de l'intensité)
ω la fréquence angulaire (ou pulsation) du signal en radians par seconde (rad.s-1) (ω = 2πf )
et ωc la fréquence de coupure (angulaire) du filtre (à -3 dB).

En normalisant l'expression (c’est-à-dire en spécifiant ωc = 1) :

G_n(\omega) = \left | H_n(j \omega) \right | = {1 \over \sqrt{ 1 + \omega ^ {2 n}} }

Les 2n-1 premières dérivées de Gn sont nulles pour ω = 0, impliquant une constance maximale du gain dans la bande passante.

Aux hautes fréquences :

{{\left | H(j \omega) \right |}_{dB}} \sim -20\times n \,\log_{10}{\omega}

Le roll-off du filtre (la pente du gain dans un diagramme de Bode) est de -20n dB/décade, où 'n' est l'ordre du filtre.

Le gain ne représente que le module de la fonction de transfert H(p) (au sens de la transformée de Laplace), ce qui laisse une certaine latitude pour déterminer cette dernière. On doit avoir

H(p)H(-p) = \frac {{G_0}^2}{1+\left (-\frac{p^2}{\omega_c^2}\right)^n}

Les pôles de cette expression sont équirépartis sur un cercle de rayon ωc. Pour que le filtre soit stable, on choisit les pôles de la fonction de transfert comme ceux de H(p)H(-p) ayant une partie réelle négative. Le k-ième pôle est donné à l'aide des racines n-ièmes de l'unité :

-\frac{p_k^2}{\omega_c^2} = (-1)^{\frac{1}{n}} = e^{\frac{j(2k-1)\pi}{n}} \qquad\mathrm{k = 1,2,3, \ldots, n}

d'où

p_k = \omega_c e^{\frac{j(2k+n-1)\pi}{2n}}\qquad\mathrm{k = 1,2,3, \ldots, n}

La fonction de transfert s'écrit en fonction de ces pôles :

H(p)=\frac{G_0}{\prod_{k=1}^n (p-p_k)/\omega_c}

Le polynôme au dénominateur est appelé polynôme de Butterworth.

n Polynôme de Butterworth Bn(p) pour ωc = 1.
1 (p + 1)
2 p2 + 1.4142p + 1
3 (p + 1)(p2 + p + 1)
4 (p2 + 0.7654p + 1)(p2 + 1.8478p + 1)
5 (p + 1)(p2 + 0.6180p + 1)(p2 + 1.6180p + 1)
6 (p2 + 0.5176p + 1)(p2 + 1.4142p + 1)(p2 + 1.9319p + 1)
7 (p + 1)(p2 + 0.4450p + 1)(p2 + 1.2470p + 1)(p2 + 1.8019p + 1)
8 (p2 + 0.3902p + 1)(p2 + 1.1111p + 1)(p2 + 1.6629p + 1)(p2 + 1.9616p + 1)

Les polynômes normalisés de Butterworth peuvent être utilisés pour déterminer les fonctions de transfert de filtre passe-bas pour toute fréquence de coupure ωc selon que:

H(p) = \frac{G_0}{B_n(a)} , où a = \frac{p}{\omega_c}

Comparaisons

Diagramme de Bode des gains d'un filtre de Butterworth, d'un filtre de Tchebychev de type 1, d'un filtre de Tchebychev de type 2 et d'un filtre elliptique

Les filtres de Butterworth sont les seuls filtres linéaires dont la forme générale est similaire pour tous les ordres (mis à part une pente différente dans la bande de coupure).

Par comparaison avec les filtres de Tchebychev ou elliptiques, les filtres de Butterworth ont un roll-off plus faible qui implique d'utiliser un ordre plus important pour une implantation particulière. Leur gain est en revanche nettement plus constant dans la bande passante.

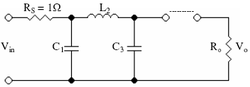
Implémentation

Schéma type d'une implémentation Cauer-1 d'un filtre de Butterworth

Un filtre de Butterworth dont on connait la fonction de transfert peut être implémenté électroniquement suivant la méthode de Cauer. Le ke élément d'un tel circuit est donné par :

C_k = 2 sin \left [\frac {(2k-1)}{2n} \pi \right ] (k impair)
L_k = 2 sin \left [\frac {(2k-1)}{2n} \pi \right ] (k pair)


Bibliographie

Notes

  1. ↑ S. Butterworth, « On the Theory of Filter Amplifiers », Wireless Engineer, vol. 7 (1930), pp. 536-541

Voir aussi

Articles connexes

Types de filtres Filtre passe-bas · Filtre passe-haut · Filtre passe-bande · Filtre coupe-bande
filtres linéaires Filtre de Bessel · Filtre de Butterworth · Filtre de Tchebychev · Filtre elliptique
filtres numériques Filtre à réponse impulsionnelle finie · Filtre à réponse impulsionnelle infinie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Filtre de Butterworth de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Filtre De Butterworth — Pour les articles homonymes, voir Butterworth. Diagramme de Bode d un filtre de Butterworth passe bas du premier ordre Un …   Wikipédia en Français

  • Filtre de butterworth — Pour les articles homonymes, voir Butterworth. Diagramme de Bode d un filtre de Butterworth passe bas du premier ordre Un …   Wikipédia en Français

  • filtre de Butterworth — Batervorto filtras statusas T sritis radioelektronika atitikmenys: angl. Butterworth filter vok. Filter mit Butterworth Verhalten, n rus. фильтр Баттерворта, m pranc. filtre de Butterworth, m …   Radioelektronikos terminų žodynas

  • Filtre De Bessel — Le filtre de Bessel, également désigné sous le nom de filtre de Thompson, est un filtre polynomial (« tout pôle ») dont la caractéristique principale est d offrir un délai constant en bande passante. Concrètement, cela signifie que… …   Wikipédia en Français

  • Filtre de bessel — Le filtre de Bessel, également désigné sous le nom de filtre de Thompson, est un filtre polynomial (« tout pôle ») dont la caractéristique principale est d offrir un délai constant en bande passante. Concrètement, cela signifie que… …   Wikipédia en Français

  • Filtre De Legendre — Le filtre de Legendre, également appelé filtre de Papoulis, du nom de son inventeur (1958), ou encore filtre optimal a été conçu pour présenter à la fois une atténuation strictement monotone (pas d ondulation, à l inverse des filtres de… …   Wikipédia en Français

  • Filtre de legendre — Le filtre de Legendre, également appelé filtre de Papoulis, du nom de son inventeur (1958), ou encore filtre optimal a été conçu pour présenter à la fois une atténuation strictement monotone (pas d ondulation, à l inverse des filtres de… …   Wikipédia en Français

  • Filtre De Tchebychev — Les filtres de Tchebychev sont un type de filtre caractérisé par l acceptation d une ondulation, ou bien en bande passante ou bien en bande atténuée. Dans le premier cas, on parle de filtres de Tchebychev de type 1 ou directs, dans le second, de… …   Wikipédia en Français

  • Filtre de tchebychev — Les filtres de Tchebychev sont un type de filtre caractérisé par l acceptation d une ondulation, ou bien en bande passante ou bien en bande atténuée. Dans le premier cas, on parle de filtres de Tchebychev de type 1 ou directs, dans le second, de… …   Wikipédia en Français

  • Filtre Passe-Bas — Image sur laquelle a été appliqué un filtre passe bas (résultat à droite) Un filtre passe bas est un filtre qui laisse passer les basses fréquences et qui atténue les hautes fréquences, c est à dire les fréquences supérieures à la fréquence de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”