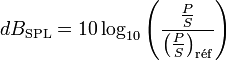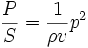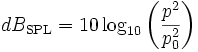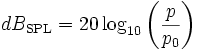Decibel

Décibel

Pour les articles homonymes, voir Décibel (homonymie).

Le décibel (dB) est une unité logarithmique de mesure du rapport entre deux puissances. C’est une grandeur sans dimension en dehors du système international^[1]. Elle est utilisée notamment dans les domaines de l’acoustique, de la physique, de l’électronique et est largement répandue dans l’ensemble des champs de l’ingénierie.

Cette unité est particulièrement pertinente dans les domaines où la perception humaine est mise en jeu. En effet la loi de Fechner stipule que la sensation ressentie varie comme le logarithme de l'excitation. On utilise notamment couramment le décibel pour exprimer des intensités sonores.

Sommaire

1 Histoire des bels et décibels
2 Définition
3 Le décibel comme unité de mesure absolue
4 Unité acoustique
5 Divers exemples sur l’échelle du bruit pour une fréquence de 1000 Hz
6 Notes et références
7 Voir aussi
- 7.1 Articles connexes
- 7.2 Liens externes

Histoire des bels et décibels

Le bel (symbole B) est utilisé dans les télécommunications, l’électronique, l’acoustique ainsi que les mathématiques. Inventé par des ingénieurs des Laboratoires Bell pour mesurer l’atténuation du signal audio sur une distance d’un mile (1,6 km), longueur standard d’un câble de téléphone, il était appelé unité de « transmission » à l’origine, ou TU ((en)Transmission unit), mais fut renommé en 1923 ou 1924 en l’honneur du fondateur du laboratoire et pionnier des télécoms, Alexander Graham Bell.

Définition

Si on appelle X le rapport de deux puissances $P 1$ et $P 0$ , la valeur de X en bel (B) s'écrit :

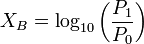
$X_{B} = \log_{10}\left({P_1\over P_0}\right)$

On peut également exprimer X dans un sous multiple du bel, le décibel (dB) :

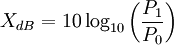
$X_{dB} = 10\log_{10}\left({P_1\over P_0}\right)$

un décibel étant égal à un dixième de bel.

Si le rapport entre les deux puissances est de : 10² = 100, cela correspond à 2 bels ou 20 dB. À titre d'exemple la puissance double environ tous les 3 décibels et 130 décibels correspondent à une puissance 1000 fois plus importante que 100 décibels.

Dans certaines situations les puissances sont proportionnelles au carré d’une autre grandeur, généralement une amplitude. En électronique linéaire et sinusoïdale la puissance est proportionnelle au carré de l'amplitude de la tension ; en acoustique, la puissance acoustique est proportionnelle au carré de l'amplitude de la pression acoustique. Si les amplitudes sont plus facilement accessible au calcul ou à l'expérience, il est souvent choisi d'exprimer le rapport de puissance en termes d'amplitude. Soit $U 1$ et $U 0$ les amplitudes correspondant respectivement à $P 1$ et $P 0$ , on a :

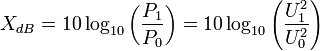
$X_{dB} = 10\log_{10}\left({P_1\over P_0}\right) = 10\log_{10}\left({U_1^2\over U_0^2}\right)$

Le logarithme du carré d'une grandeur étant égal à deux fois le logarithme de la grandeur on obtient la formule suivante :

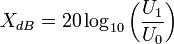
$X_{dB} = 20\log_{10}\left({U_1\over U_0}\right)$

Le décibel comme unité de mesure absolue

Le décibel est utilisé comme mesure du rapport entre deux puissances dans certains domaines, comme les télécommunications ou le radar pour décrire des gains ou des amplifications (dB positifs) ou des pertes ou des atténuations (dB négatifs). On parle alors d’une atténuation de 15 dB compensée par un amplificateur avec 15 dB de gain. Une atténuation de 15 dB est équivalente à un gain de -15 dB.

Le décibel a donné naissance à un certain nombre d’unités (sans dimensions) utilisées pour mesurer des puissances ou des intensités de façon absolue. Ceci se fait en utilisant comme puissance de référence (dans le dénominateur de la définition précédente) une valeur de puissance prédéfinie. Dans ce cas, on ajoute une lettre à « dB » pour savoir de quoi on parle. Voici quelques exemples :

dBSPL décibel en acoustique (voir plus bas) ;
dB(A) décibel pondéré en acoustique à 40 dB au-dessus du seuil d'audibilité (voir plus bas) ;
dB(B) décibel pondéré en acoustique à 70 dB par rapport au seuil d'audibilité ;
dB(C) pareillement que la référence dB(B) mais cette fois-ci à 90 dB par rapport au seuil d'audibilité ;
dBFS échelle de mesure en numérique, le niveau maximum mesuré est le Zéro Fullscale, voir: (en)dBFS
dBW décibels au-dessus d’un watt. La puissance de référence est 1 W ;
dBm décibels au-dessus d’un milliwatt. La puissance de référence est 1 mW ;
dBV décibels mesurant la tension par rapport à une référence de 1 volt RMS. Le matériel audio grand-public travaille généralement au niveau électrique de -10 dBV, soit 0,3162 V (ou -7,78 dBu) ;
dBμV décibels mesurant la tension par rapport à une référence de 1 μvolt RMS.;
dBu décibels mesurant la tension par rapport à une référence de 0,775 volts RMS. Cette valeur de référence correspond à la tension d’une charge de 600 ohms soumise à 1 mW. Le matériel audio professionnel travaille généralement au niveau électrique de +4 dBu, soit 1,228 V (ou 1,78 dBV) ;
dBi utilisé pour parler du gain des antennes. Le gain de référence est celle d’une antenne isotrope ;
dBd : pareillement que le dBi mais le gain de référence est celle d'une antenne dipole ;
dBFs : amplitude d’un signal comparativement à son niveau maximum avant saturation ;
dBZ : mesure du rapport entre la réflectivité (Z) revenant de la précipitation sondée par un radar météorologique par mètre cube (qui est proportionnelle au diamètre à la sixième puissance des gouttes) et la réflectivité qu'on aurait si ce volume était rempli de 1 $mm 6 / m 3$ de gouttes.

Unité acoustique

dBSPL

Le décibel, de symbole dB, est une unité relative de l’intensité acoustique. Le dBSPL (Sound Pressure Level) est défini par le rapport de la puissance par unité de surface du son que l’on mesure et une puissance par unité de surface de référence :

$dB_\mathrm{SPL} = 10 \log_{10}{ \left({ {P\over S} \over \left({P\over S}\right)_\mathrm{r\acute{e}f} }\right)} \$

La puissance par unité de surface de référence est 10^-12 W·m^-2 (un picowatt par mètre carré).

La puissance par unité de surface transportée par une onde sonore est reliée à la pression acoustique par la formule :

${P\over S} = {1\over \rho v}p^2$

où :

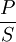$\frac{P}{S}$ est la puissance par unité de surface ou intensité acoustique(en W·m^-2).
$p$ est la pression acoustique efficace (en pascal).
$ρ$ est la masse volumique du milieu (en kg·m^-3).
$v$ est la vitesse du son dans le milieu (en m·s^-1).

Si, dans la formule de la première définition, on remplace la puissance par unité de surface par la formule en fonction de la pression acoustique, la densité et la vitesse se simplifient et on obtient :

$dB_\mathrm{SPL} = 10 \log_{10}\bigg(\frac{p^2}{p_0^2}\bigg) \$

Si on sort le carré du logarithme on obtient la seconde version de la définition de dBSPL :

$dB_\mathrm{SPL} = 20 \log_{10} \bigg(\frac{p}{p_0}\bigg) \$

$p$ est le niveau de pression du son (en valeur efficace) et 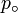$\textstyle{ p_\circ}$ est la pression de référence que l’on accepte comme le niveau à partir duquel l’oreille humaine commence à percevoir un son pur de 1 kHz. Celui-ci est de 20 µPa (valeur efficace). Les deux valeurs de référence (1 picowatt par mètre carré et 20 µPa efficaces) sont équivalentes pour l’air à la température et pression ambiante.

Par ailleurs, pour un même niveau acoustique à différentes fréquences, l’homme ne perçoit pas le même niveau d’intensité. Pour un même niveau d’intensité acoustique de 20 dBSPL, un son pur de 1 kHz paraîtra plus fort qu’un son de 10 kHz tandis qu’un son de 100 Hz ne sera pas perçu. Pour avoir le même niveau perçu, le son de 10 kHz devra être à 30 dBSPL et le son de 100 Hz à 50 dBSPL. Les courbes isosoniques représentent les courbes de même intensité perçue qu’un son pur de 1 kHz à un niveau acoustique donné.

dBHL

Intensité perçue par l'oreille humaine normale.

dBSL

Intensité perçue par un individu donné.

Le seuil de perception auditive

Le niveau de 0 phone ou 0 dB SPL est un niveau vraiment bas. Pour s’en rendre compte, voici à quoi ce niveau de 0 dB SPL correspond :

en puissance par mètre carré : à 0,5 watts repartis sur toute la surface de la France métropolitaine ;
en pression : à la pression due au poids d’une couche de 2×10^-9 m d’eau (environ 20 atomes d’épaisseur) ;
en déplacement des molécules dans l’air : à une oscillation (crête à crête) de 2×10^-11 m, c’est-à-dire 2 dixièmes de l’épaisseur d’un atome.

dB pondéré

Il existe plusieurs courbes de pondération: A, B, et C. La courbe de pondération (A) correspond de prés à la correction de l'oreille humaine. Moins sensible aux BF (basses fréquences) et plus sensibles aux HF (hautes fréquences). Cependant ce n'est pas encore ce que déchiffre notre cerveau. Pour cela, il est impératif d'additionner les niveaux sonores pondérés relevés en fonctions des fréquences. Attention, 80 dB (A) + 80 dB(a) n'est pas égal à 160 dB(A) mais à 83 dB(A). Plus la différence entre deux sons est élevée moins on majore. Le bruit d'un avion 120 dB (A)+ le bruit d'une voiture 80 dB(A)= 120 dB(A). L'avion couvre complètement le bruit de la voiture. Pour bien comprendre Le dB(A) est un niveau sonore global (Son perçu par l'oreille)et le dB est un niveau sonore qui n'a de vrai valeur que lorsqu'il est noté pour une fréqunce donnée.

Pour prendre en compte cette sensibilité de l’oreille par rapport aux fréquences, le dB(A) est utilisé. En effet, celui-ci utilise la courbe isosonique, correspondant à un niveau perçu de 40 dB pour un son pur de 1 kHz. L’inverse de cette courbe pondère le signal et l’on obtient le niveau en dB(A) par intégration sur toutes les fréquences. Cette unité est très fréquemment utilisée dans les indicateurs acoustiques du bruit.

Divers exemples sur l’échelle du bruit pour une fréquence de 1000 Hz

0 dB : seuil d'audibilité
De 0 à 10 dB : désert
De 10 à 20 dB : cabine de prise de son
De 20 à 30 dB : conversation à voix basses, chuchotement
De 30 à 40 dB : forêt
De 40 à 50 dB : bibliothèque, lave-vaisselle
De 50 à 60 dB : lave-linge
De 60 à 70 dB : sèche-linge, sonnerie de téléphone, téléviseur, conversation courante
De 70 à 80 dB : aspirateur, restaurant bruyant, passage d'un train à 80 km/h
De 80 à 90 dB : tondeuse à gazon, klaxon de voiture
De 90 à 100 dB : route à circulation dense, tronçonneuse, atelier de forgeage, TGV à 300 km/h à 25 m
De 100 à 110 dB : marteau-piqueur à moins de 5 mètres dans une rue, discothèque
De 110 à 120 dB : tonnerre, atelier de chaudronnerie
De 120 à 130 dB : sirène d'un véhicule de pompier, avion au décollage (à 300 mètres), concert amplifié
130 dB : seuil de la douleur
De 140 à 150 dB : course de Formule 1, avion au décollage
170 dB : fusil d'assaut
180 dB : décollage de la fusée Ariane, lancement d'une roquette
194 dB : son le plus bruyant possible dans l'air à la pression atmosphérique du niveau de la mer. La différence de pression dans une onde sonore de ce niveau est d'une atmosphère et correspond à l'apparition d'une pression nulle sur le front de dépression de l'onde. Toute onde au-delà de cette frontière ne s'appelle plus onde sonore mais onde de choc.

Au-dessous de 20 dB, le son est pratiquement inaudible pour l’oreille humaine. Il commence à devenir douloureux au-delà de 80 dB, dangereux à partir de 100 dB et insupportable dès 120 dB. Le seuil de douleur n'est bien entendu pas un absolu, il dépend de la fréquence. Le seuil de douleur peut être atteint à un niveau sonore de 110 dB pour une fréquence de 20000 Hz et à 120 dB pour une fréquence de inférieure à 10000 Hz. Ces valeurs (80 dB, 100 dB, 120 dB) sont les valeurs courantes de la littérature.

Des tests psycho-acoustiques ont montré qu'un dépassement du volume sonore est perceptible par l'oreille humaine à partir de 1 dB et qu'un écart de 10 dB est perçu par l'oreille humaine comme un doublement du volume sonore.^[2]

Notes et références

Voir aussi

Liens externes

Portail de l’électricité et de l’électronique
Portail de la physique

Ce document provient de « D%C3%A9cibel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Decibel de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires: