- Filtre numerique
-
Filtre numérique
En électronique, un filtre numérique est un élément qui effectue un filtrage à l'aide d'une succession d'opérations mathématiques sur un signal discret. C'est-à-dire qu'il modifie le contenu spectral du signal d'entrée en atténuant ou éliminant certaines composantes spectrales indésirées. Contrairement aux filtres analogiques, qui sont réalisés à l'aide d'un agencement de composantes physiques (résistance, condensateur, inductance, transistor, etc.), les filtres numériques sont réalisés soit par des circuits intégrés dédiés, des processeurs programmables (FPGA, microprocesseur, DSP, microcontrôleur, etc.), soit par logiciel dans un ordinateur.
Les filtres numériques peuvent, en théorie, réaliser la totalité des effets de filtrage pouvant être définis par des fonctions mathématiques ou des algorithmes. Les deux principales limitations des filtres numériques sont la vitesse et le coût. La vitesse du filtre est limitée par la vitesse (l'horloge, le "clock" en anglais) du processeur. Pour ce qui est du coût, celui-ci dépend du type de processeur utilisé. Par contre, le prix des circuits intégrés ne cesse de diminuer, et les filtres numériques se retrouvent partout dans notre environnement, radio, téléphone cellulaire, télévision, lecteurs MP3, etc.
Les filtres numériques étant généralement réalisés par des processeurs, ils sont définis à l'aide de langages de programmation.
Sommaire
Définition
Un filtre numérique peut être défini par une équation aux différences, c'est-à-dire l'opération mathématique du filtre dans le domaine temporel (discret).
La forme générale du filtre d'ordre M est la suivante :
![y[n] = {\sum_{k=0}^N} b_k \cdot x[n-k] - {\sum_{k=1}^M} a_k \cdot y[n-k]](/pictures/frwiki/50/2464d0b9c1beb3b25b5359ccd12116e6.png)
![y[n] = b_0 \cdot x[n] + b_1 \cdot x[n-1] + b_2 \cdot x[n-2] + .... + b_N \cdot x[n-N] - a_1 \cdot y[n-1] - a_2 \cdot y[n-2] + .... + a_M \cdot y[n-M]](/pictures/frwiki/53/5289f1a5e6d91364692acf470ef34bb1.png)
Une fonction de transfert, dans le domaine fréquentiel (Transformée en Z), permet également de définir un filtre numérique. Ainsi, la fonction de transfert générale d'ordre N d'un filtre numérique est la suivante :
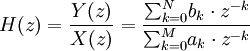
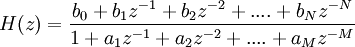
La valeur des coefficients a et b fixera le type de filtre, passe-bas, passe-haut, etc.
Classification
FIR - Filtre à réponse impulsionnelle finie
Il y a deux grandes familles de filtres numériques : la première, les filtres FIR, de l'anglais "Finite Impulse Response" (Filtre à réponse impulsionnelle finie). Ce type de filtre est dit fini, car sa réponse impulsionnelle se stabilisera ultimement à zéro. Un filtre FIR est non récursif, c'est-à-dire que la sortie dépend uniquement de l'entrée du signal, il n'y a pas de contre-réaction. Ainsi, les coefficients a de la forme générale des filtres numériques sont tous égaux à zéro.
Une propriété importante des filtres FIR est que les coefficients du filtre b sont égaux à la réponse impulsionnelle h du filtre. D'autre part, la forme temporelle du filtre est tout simplement la convolution du signal d'entrée x avec les coefficients (ou réponse impulsionnelle) b (ou h).
Un exemple de filtre FIR simple est une moyenne. Effectivement, effectuer la moyenne sur une série de données est équivalent à appliquer un filtre FIR à coefficient constant 1/N.
Voici un exemple de l'implémentation d'un filtre FIR en C/C++ dans le domaine temporel :
// si la taille de NB_COEF = 2^n utiliser un masque au lieu du modulo (%) // %=NB_COEF => &=(NB_COEF-1) // pipe est un buffer circulaire #define NB_COEF 16 // nombre de coef du filtre double x_buffer[NB_COEF]={0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}; double coef[NB_COEF]={0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}; int ptr_x_buffer=0; double FiltreFIR(double x) // x: Signal d'entrée // y: Signal de sortie { int n, y=0; x_buffer[ptr_x_buffer++] = x; ptr_x_buffer %= NB_COEF; for( n = (NB_COEF-1) ; n >= 0 ; n-- ) { y += coef[n] * x_buffer[ptr_x_buffer++]; ptr_x_buffer %= NB_COEF; } return(y); }
IIR - Filtre à réponse impulsionnelle infinie
En opposition, les filtres de la seconde famille, les IIR, de l'anglais "Infinite Impulse Response" (Filtre à réponse impulsionnelle infinie) possèdent une réponse impulsionnelle qui ne se stabilisera jamais, et ce, même à l'infini. Ce type de filtre est récursif, c'est-à-dire que la sortie du filtre dépend à la fois du signal d'entrée et du signal de sortie, il possède ainsi une boucle de contre-réaction ("feedback"). Les filtres IIR sont principalement la version numérique des filtres analogiques traditionnels : Butterworth, Tchebychev, Bessel, Elliptique.
Voir aussi
Liens externes
Filtre numérique par la pratique
- Portail de l’électricité et de l’électronique
- Portail de l’informatique
Catégorie : Filtre
Wikimedia Foundation. 2010.
