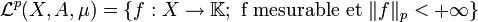Espace de Lebesgue

Espace Lp

En mathématiques, les espaces L^p sont des espaces de fonctions dont la puissance p-ième de la fonction est intégrable, au sens de Lebesgue.

Les espaces L^p sont très utilisés en analyse (et particulièrement en analyse fonctionnelle), puisqu'ils n'imposent aux fonctions manipulées qu'une régularité relativement faible (l'intégrabilité), sans par exemple demander de la continuité ou de la dérivabilité.

Sommaire

1 Définition formelle
- 1.1 Espaces L^p
- 1.2 Espace L^∞
2 Exemples
3 Propriétés
- 3.1 Espaces duals
4 Voir aussi

Définition formelle

Avant de définir les espaces $L p$ , on définit généralement les espaces 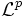$\mathcal L^p$ (qui ne sont cependant presque pas utilisés en dehors de cette définition).

Espaces L^p

Pour tout réel p supérieur ou égal à 1, l'espace 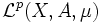$\mathcal L^p(X,A,\mu)$ est l'espace vectoriel des fonctions à valeurs réelles (ou complexes selon les choix d'auteur), définies et mesurables sur l'espace mesuré (X,A,μ) et dont la p-ième puissance est μ-intégrable. On définit 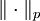$\|\cdot\|_p$ comme :

$\|f\|_p = {\left[\int_X|f|^p \,d\mu\right]}^{1/p}$ .

Autrement dit,

$\mathcal L^p(X,A,\mu) = \left\{ f:X\rightarrow\mathbb K ; \mbox{ f mesurable et } \|f\|_p < +\infty \right\}$

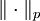Cet espace est un espace vectoriel semi-normé car deux fonctions qui ne diffèrent que d'un ensemble de mesure nulle ont la même semi-norme $\|\cdot\|_p$ .

L'espace $L p (X, A,μ)$ est ensuite défini comme l'espace vectoriel quotient de 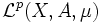$\mathcal L^p(X,A,\mu)$ par la relation d'équivalence « f ~ g » ssi « f et g sont égales presque partout ». Ainsi, 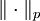$\|\cdot\|_p$ est une norme sur $L p (X, A,μ)$ .

Dans la théorie de Riemann, l'espace L^p(R) se définit par un procédé de complétion.

Espace L^∞

Article détaillé : Espace L∞.

L'espace 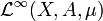$\mathcal L^\infty(X,A,\mu)$ est défini comme l'espace vectoriel des fonctions μ-essentiellement bornées (c'est-à-dire les fonctions bornées presque partout).

Ensuite, l'espace 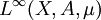$L^\infty(X,A,\mu)$ est l'espace vectoriel quotient de 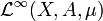$\mathcal L^\infty(X,A,\mu)$ par la relation d'équivalence « f ~ g » ssi « f et g sont égales presque partout ».

Exemples

Si X est l'ensemble N des entiers naturels, muni de la tribu grossière, et que μ est la mesure de comptage, l'espace $L p (X, A,μ)$ n'est autre que l'espace l^p(N) des suites réelles dont la p-ième puissance est sommable.

Avec X = R, A la tribu des boréliens et $μ$ la mesure de Lebesgue

la fonction 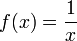$f(x) = \frac{1}{x}$ définie sur 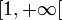$[1,+\infty[$ est dans $L 2$ , mais pas dans $L 1$ ;
la fonction 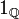$1_\Q$ , définie sur R, qui vaut 1 sur les rationnels et 0 ailleurs, est dans 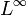$L^\infty$ et est égale, dans 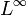$L^\infty$ , à la fonction constante $0$ ; du fait que les rationnels sont de mesure nulle dans R.

Propriétés

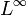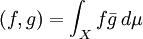Les espaces $L p$ (pour p ≥ 1) et $L^\infty$ sont des espaces de Banach et l'espace $L 2$ est un espace de Hilbert lorsqu'on le munit du produit scalaire $(f,g) = \int_X f \bar g \,d\mu$ .
En général, si 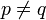$p \neq q$ , on n'a ni L^p inclus dans L^q, ni L^q inclus dans L^p.

Cependant si la mesure est finie (comme en probabilités par exemple), alors pour p < q, L^q est inclus dans L^p.

D'autre part s'il existe ε > 0 tel que toute partie non vide de X est de mesure plus grande que ε, pour p < q, L^p est inclus dans L^q.

Espaces duals

Pour 1 < p < +∞, l'espace dual de $L p$ est $L q$ , où q est défini de façon que 1/p + 1/q = 1.

Voir aussi

Portail des mathématiques

Ce document provient de « Espace Lp ».

Catégorie : Espace fonctionnel remarquable

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace de Lebesgue de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Espace De Sobolev — Les espaces de Sobolev sont des espaces fonctionnels. Plus précisément, un espace de Sobolev est un espace vectoriel de fonctions muni de la norme obtenue par la combinaison de la norme norme Lp de la fonction elle même ainsi que de ses dérivées… … Wikipédia en Français
Espace de sobolev — Les espaces de Sobolev sont des espaces fonctionnels. Plus précisément, un espace de Sobolev est un espace vectoriel de fonctions muni de la norme obtenue par la combinaison de la norme norme Lp de la fonction elle même ainsi que de ses dérivées… … Wikipédia en Français
Espace de Sobolev — Les espaces de Sobolev sont des espaces fonctionnels. Plus précisément, un espace de Sobolev est un espace vectoriel de fonctions muni de la norme obtenue par la combinaison de la norme norme Lp de la fonction elle même ainsi que de ses dérivées… … Wikipédia en Français
LEBESGUE (H.) — Le mathématicien Henri Lebesgue est l’un des fondateurs de l’analyse moderne. Presque tous ses travaux se rattachent à la théorie des fonctions de variables réelles. Sa conception de l’intégration et de la mesure renouvelle l’étude des problèmes… … Encyclopédie Universelle
Espace Séparable — En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous ensemble dénombrable et dense, c est à dire si l on peut trouver un ensemble dénombrable de points dont l adhérence est égale à l… … Wikipédia en Français
Espace separable — Espace séparable En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous ensemble dénombrable et dense, c est à dire si l on peut trouver un ensemble dénombrable de points dont l… … Wikipédia en Français
Espace Vectoriel — En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée… … Wikipédia en Français
Espace vectoriel linéaire — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… … Wikipédia en Français
Espace Préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Le cas… … Wikipédia en Français
Espace Vectoriel Normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace de Lebesgue

Espace Lp

Sommaire