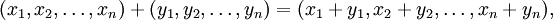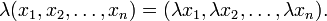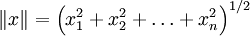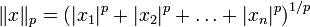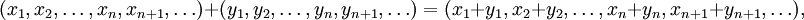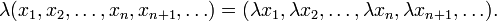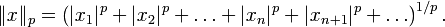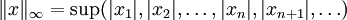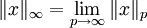Espace De Suites Lp

Espace de suites lp

En mathématiques, l'espace 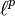$\ell^p$ est un espace de suites à valeurs réelles ou complexes qui possède une structure d'espace de Banach.

Motivation

Considérons l'espace des vecteurs réels $\mathbb{R}^n$ . La somme de vecteurs dans $\mathbb{R}^n$ est donnée par :

$(x_1, x_2, \dots, x_n) + (y_1, y_2, \dots, y_n) = (x_1+y_1, x_2+y_2, \dots, x_n+y_n),$

Et la multiplication par un scalaire est donnée par:

$\lambda(x_1, x_2, \dots, x_n)=(\lambda x_1, \lambda x_2, \dots, \lambda x_n).$

La norme d'un vecteur 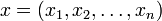$x=(x_1, x_2, \dots, x_n)$ est souvent donnée par:

$\|x\|=\left(x_1^2+x_2^2+\dots+x_n^2\right)^{1/2}$

Mais se n'est pas la seule façon de définir une norme, si p est un nombre réel et p≥1 nous pouvons définir:

$\|x\|_p=\left(|x_1|^p+|x_2|^p+\dots+|x_n|^p\right)^{1/p}$

Pour chaque vecteur 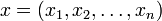$x=(x_1, x_2, \dots, x_n)$ . Il s'avère que cette définition satisfait les propriétés d'une norme. Donc pour chaque p≥1, $\mathbb{R}^n$ ensemble et la p-norme que nous venons de définir nous formons un espace de Banach.

Espace $\ell^p$

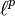
La p-norme peut être étendue aux vecteurs ayant une infinité de composantes ce qui nous donne l'espace 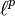$\ell^p$ . Pour 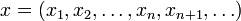$x=(x_1, x_2, \dots, x_n, x_{n+1},\dots)$ , une séquence infinie de nombre réels ou complexes nous définissons la somme:

$(x_1, x_2, \dots, x_n, x_{n+1},\dots)+(y_1, y_2, \dots, y_n, y_{n+1},\dots)=(x_1+y_1, x_2+y_2, \dots, x_n+y_n, x_{n+1}+y_{n+1},\dots),$

Et la multiplication par un scalaire:

$\lambda(x_1, x_2, \dots, x_n, x_{n+1},\dots) = (\lambda x_1, \lambda x_2, \dots, \lambda x_n, \lambda x_{n+1},\dots).$

Nous définissons la p-norme:

$\|x\|_p=\left(|x_1|^p+|x_2|^p+\dots+|x_n|^p+|x_{n+1}|^p+\dots\right)^{1/p}.$

Mais ici un problème survient, c'est que la série de droite n'est pas toujours convergente, par exemple, la série $(1,1,1,...)$ a une p-norme infinie pour n'importe quel p. Donc l'espace 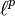$\ell^p$ est défini comme l'ensemble des séquences infinies de nombres réels ou complexes dont la p-norme est définie.

On définit aussi la ∞-norme comme:

$\|x\|_\infty=\sup(|x_1|, |x_2|, \dots, |x_n|,|x_{n+1}|, \dots)$

et l'espace correspondant 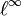$\ell^\infty$ de tous les vecteurs ou séquences bornées. De plus on a:

$\|x\|_\infty=\lim_{p\to\infty}\|x\|_p$

Voir aussi

Espace L^p de fonctions

Portail des mathématiques

Ce document provient de « Espace de suites lp ».

Catégorie : Suite

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace De Suites Lp de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Espace de suites lp — En mathématiques, l espace est un espace de suites à valeurs réelles ou complexes qui possède une structure d espace de Banach. Motivation Considérons l espace des vecteurs réels . La somme de vecteurs dans est donnée par … Wikipédia en Français
Espace de suites ℓp — En mathématiques, l espace est un certain espace de suites à valeurs réelles ou complexes qui possède une structure d espace de Banach. Motivation Considérons l espace vectoriel réel , i.e. l espace des n uplets de nombres réels. La norme… … Wikipédia en Français
Espace Vectoriel Normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… … Wikipédia en Français
Espace normé — Espace vectoriel normé Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach,… … Wikipédia en Français
Espace vectoriel norme — Espace vectoriel normé Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach,… … Wikipédia en Français
Espace De Fréchet — L espace de Fréchet au sens de la topologie générale est décrit à l article Espace T1. Un espace de Fréchet est une structure mathématique d espace vectoriel topologique satisfaisant certains théorèmes relatifs aux espaces de Banach même en l… … Wikipédia en Français
Espace de Frechet — Espace de Fréchet L espace de Fréchet au sens de la topologie générale est décrit à l article Espace T1. Un espace de Fréchet est une structure mathématique d espace vectoriel topologique satisfaisant certains théorèmes relatifs aux espaces de… … Wikipédia en Français
Espace de fréchet — L espace de Fréchet au sens de la topologie générale est décrit à l article Espace T1. Un espace de Fréchet est une structure mathématique d espace vectoriel topologique satisfaisant certains théorèmes relatifs aux espaces de Banach même en l… … Wikipédia en Français
Espace De Hilbert — Un espace de Hilbert est un espace de Banach (donc complet) dont la norme ∥·∥ découle d un produit scalaire ou hermitien <·,·> par la formule . C est la généralisation en dimension quelconque d un espace euclidien ou hermitien. Théorème de… … Wikipédia en Français
Espace de Lebesgue — Espace Lp En mathématiques, les espaces Lp sont des espaces de fonctions dont la puissance p ième de la fonction est intégrable, au sens de Lebesgue. Les espaces Lp sont très utilisés en analyse (et particulièrement en analyse fonctionnelle),… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace De Suites Lp