Espace connexe par arcs

Connexité par arcs

En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En fait, la connexité est la notion fondamentale. Mais la connexité par arcs est plus intuitive, et se trouve être très souvent la meilleure façon de prouver la connexité.

Sommaire

1 Chemins
- 1.1 Chemins dans un espace topologique
- 1.2 Chemins dans un espace vectoriel normé
2 Connexité par arcs
3 Voir aussi

Chemins

Avant de définir la connexité par arcs il faut définir ce qu'on appelle « relier par un chemin ». Selon le cadre où l'on se trouve on peut considérer des chemins particuliers.

Chemins dans un espace topologique

Si $E$ est un espace topologique et si $x$ et $y$ sont deux points de $E$ , on appelle chemin d'origine $x$ et d'extrémité $y$ toute application continue $\gamma : [0,1] \rightarrow E$ telle que $γ(0) = x$ et $γ(1) = y$ .

On dit que $x$ et $y$ sont reliés si et seulement s’il existe un chemin d'origine $x$ et d'extrémité $y$ .

La relation « $x$ est relié à $y$ » est une relation d'équivalence sur $E$ .

Démonstration

$x$ est relié à $x$ , grâce au chemin constant $γ(t) = x$ pour tout $t \in [0,1]$ ;
si $x$ est relié à $y$ alors $y$ est relié à $x$ , grâce au chemin opposé 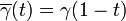$\overline{\gamma}(t) = \gamma (1-t)$ pour tout $t \in [0,1]$ ;
si $x$ est relié à $y$ et $y$ est relié à $z$ alors $x$ est relié à $z$ . En effet, si $γ 1$ relie $x$ à $y$ et $γ 2$ relie $y$ à $z$ alors le chemin composé 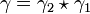$\gamma = \gamma_2 \star \gamma_1$ défini par $γ(t) = γ 1 (2 t)$ si 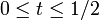$0 \leq t \leq 1/2$ et $γ(t) = γ 2 (2 t - 1)$ si 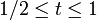$1/2 \leq t \leq 1$ relie $x$ à $z$ .

Chemins dans un espace vectoriel normé

Dans le cas où l'espace ambiant $E$ est un espace vectoriel normé, on peut préciser la nature des chemins qui relient les points.

Chemins rectilignes : un chemin est dit rectiligne si et seulement s'il peut s'écrire 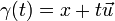$\gamma(t) = x + t \vec{u}$ pour tout $t \in [0,1]$ . Le vecteur $\vec{u}$ est appelé vecteur directeur de $γ$ . Le support du chemin est alors un segment de droite.

Chemins polygonaux : un chemin est dit polygonal si et seulement s’il s'écrit comme un composé d'un nombre fini de chemins rectilignes. Par exemple, un trajet dans Manhattan est un chemin polygonal.

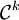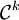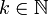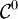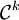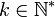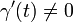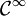Chemins de classe $\mathcal{C}^k$ : un chemin peut être de classe $\mathcal{C}^k$ avec $k \in \N$ . En fait tout chemin est de classe $\mathcal{C}^0$ c'est-à-dire continu, mais on peut avoir des niveaux de régularité supérieurs. Un chemin de classe $\mathcal{C}^k$ avec $k \in \N^*$ sera dit de plus régulier si $\gamma ' (t) \neq 0$ pour tout $t \in [0,1]$ . Un chemin régulier de classe $\mathcal{C}^{\infty}$ est dit chemin lisse.

Connexité par arcs

Ces différents types de chemins vont permettre de définir différents types de connexité par arcs selon les cas.

Définition

Deux points quelconques peuvent être reliés par un chemin tracé dans cette partie

Un espace topologique $E$ est dit connexe par arcs si et seulement si tout couple de points de $E$ est relié par un chemin.

Une partie $A$ de $E$ est dite connexe par arcs si et seulement si tout couple de points de $A$ est relié par un chemin restant dans $A$ .

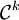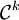Une partie $A$ d'un espace vectoriel normé est dite connexe par arcs polygonaux (respectivement par arcs $\mathcal{C}^k$ ) si deux points quelconques de $A$ peuvent être reliés par un chemin polygonal (respectivement de classe $\mathcal{C}^k$ ).

Lien avec la connexité

En apparence la connexité par arcs est très proche de la connexité ; on pourrait croire que « pouvoir toujours relier deux points » est équivalent à « être d'un seul tenant ». En fait on peut seulement affirmer : tout espace connexe par arcs est connexe.

La différence est subtile, et il est difficile d'exhiber un contre-exemple pour invalider la réciproque. Voici un contre-exemple classique. On définit une fonction $f$ par

$\begin{array}{r|ccc}f : & ]0,1] & \longrightarrow & \R \\ & x & \longmapsto & \displaystyle \cos \left( \frac{1}{x} \right). \end{array}$

Cette fonction est continue sur $]0,1]$ . On note $\Gamma = \{ (x,f(x)) | x \in ]0,1] \}$ le graphe de $f$ et on note $C = \overline{\Gamma} = \Gamma \cup \left( \{ 0 \} \times [-1,1] \right)$ l'adhérence de $Γ$ .

Alors $Γ$ est connexe comme graphe d'une fonction continue, $C$ est connexe comme adhérence d'une partie connexe. Mais on peut montrer que $C$ n'est pas connexe par arcs.

Cependant tout ouvert connexe d'un espace vectoriel normé est connexe par arcs.

Démonstration

Soit U un ouvert connexe d'un espace vectoriel topologique, x un point de U et V la composante connexe par arcs contenant x. V est non vide car il contient x. Soit y un point de V, il existe une boule B de rayon strictement positif et inclus dans U car U est ouvert. Tout point de B est connecté par arcs à y dans B. On en déduit que B est dans la composante connexe de y, donc de x, ce qui montre que B est inclus dans V et que V est ouvert.

Montrons que V est fermé. Soit z un élément de l'adhérence de V dans U. Il existe une boule B de rayon strictement positif et inclus dans U car U est ouvert. Comme zest élément de l'adhérence de V, il existe dans B un point y de V. Les points y et z sont dans la même composante connexe, car ils sont tout deux dans une boule incluse dans U. On en déduit que z est élément de V et que V est fermé.

L'ensemble V est non vide, ouvert et fermé, il est donc égal à U car U est connexe.

La démonstration précédente se généralise à tout ouvert connexe d'une variété topologique qui est donc connexe par arcs.

Lien avec la continuité

La connexité par arcs, comme la connexité, est conservée par les applications continues. Si $E$ et $F$ sont deux espaces topologiques, et si 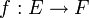$f : E \rightarrow F$ est une application continue, alors pour toute partie connexe par arcs $X$ de $E$ , l'image $f (X)$ est elle aussi connexe par arcs.

Démonstration

Si 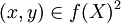$(x,y) \in f(X)^2$ , alors il existe $a$ et $b$ dans $X$ tels que $x = f (a)$ et $y = f (b)$ . L'ensemble $X$ étant connexe par arcs, il existe un chemin $\gamma : [0,1] \rightarrow X$ reliant $a$ à $b$ . L'application composée $\gamma' = f \circ \gamma : [0,1] \rightarrow f(X)$ est continue, et relie $x$ à $y$ , ce qui montre que $f (X)$ est connexe par arcs.

On a des résultats similaires pour les types plus spécifiques de connexités par arcs :

la connexité par arcs polygonaux est conservée par les applications linéaires et par les applications affines ;
la connexité par arcs 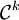$\mathcal{C}^k$ est conservée par les 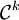$\mathcal{C}^k$ -difféomorphismes.

Produit

Soient E et F deux espaces topologiques connexes par arcs :

Le produit cartésien ExF, munis de la la topologie produit, est connexe par arcs.

S'en persuader est chose aisée. Soit (x₁, y₁) et (x₂, y₂) deux points de ExF. La connexité par arcs de E et F montre l'existence de deux chemins $γ x$ et $γ y$ à valeurs dans E et F tels que : $γ x (0) = x 1$ , $γ x (1) = x 2$ , $γ y (0) = y 1$ et $γ y (1) = y 2$ . Le chemin $γ$ , qui à t, un nombre réel compris entre 0 et 1, associe $(γ x (t),γ y (t))$ , montre la connexité par arcs de l'espace produit.

Exemples

Dans un espace vectoriel normé, une partie convexe ou étoilée est connexe par arcs.
Un cercle est connexe par arcs 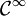$\mathcal{C}^{\infty}$ lisses mais pas par arcs polygonaux.
Un carré est connexe par arcs polygonaux mais pas par arcs 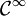$\mathcal{C}^{\infty}$ lisses.
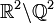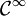Le plan privé des points à coordonnées rationnelles : $\R^2 \backslash {\mathbb Q}^2$ est connexe par arcs polygonaux et même connexe par arcs $\mathcal{C}^{\infty}$ .
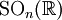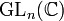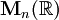Le groupe spécial orthogonal $\mathrm{SO}_{n}(\mathbb{R})$ et le groupe général linéaire $\mathrm{GL}_{n}(\mathbb{C})$ sont connexes par arcs (pour la topologie induite par une norme sur $\mathbf{M}_{n}(\mathbb{R})$ ).

Voir aussi

Portail des mathématiques

Ce document provient de « Connexit%C3%A9 par arcs ».

Catégorie : Topologie générale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace connexe par arcs de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Connexe par arcs — Connexité par arcs En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés … Wikipédia en Français
Espace localement connexe par arcs — En mathématiques, plus précisément en topologie, un espace localement connexe par arcs est un espace topologique possédant une base d ouverts dont chacun est connexe par arcs. Définition équivalente Un espace X est localement connexe par arcs si… … Wikipédia en Français
Espace Localement Connexe Par Arcs — Définition d un espace localement connexe Soit un espace topologique. On dit que est localement connexe par arcs si tout voisinage de tout point de contient un voisinage connexe par arcs de … Wikipédia en Français
Espace connexe — Connexité (mathématiques) Pour les articles homonymes, voir Connexité. Un archipel, comme celui des îles Canaries, n est pas connexe : il n est pas possible de passer à pied sec d une île à l autre. Les îles sont les composantes connexes … Wikipédia en Français
Connexite par arcs — Connexité par arcs En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés … Wikipédia en Français
Connexité Par Arcs — En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En… … Wikipédia en Français
Connexité par arcs — En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En… … Wikipédia en Français
Espace localement connexe — Le « peigne » (en) est connexe, mais pas localement connexe. En mathématiques, plus précisément en topologie, un espace localement connexe est … Wikipédia en Français
Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… … Wikipédia en Français
Espace localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Espace connexe par arcs

Connexité par arcs

Sommaire

Chemins

Chemins dans un espace topologique

Chemins dans un espace vectoriel normé

Connexité par arcs

Définition

Lien avec la connexité

Lien avec la continuité

Produit

Exemples

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Espace connexe par arcs

Connexité par arcs

Sommaire

Chemins

Chemins dans un espace topologique

Chemins dans un espace vectoriel normé

Connexité par arcs

Définition

Lien avec la connexité

Lien avec la continuité

Produit

Exemples

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link