Espace Localement Connexe Par Arcs
- Espace Localement Connexe Par Arcs
-
Espace localement connexe par arcs
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace Localement Connexe Par Arcs de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace localement connexe par arcs — En mathématiques, plus précisément en topologie, un espace localement connexe par arcs est un espace topologique possédant une base d ouverts dont chacun est connexe par arcs. Définition équivalente Un espace X est localement connexe par arcs si… … Wikipédia en Français
Espace localement connexe — Le « peigne » (en) est connexe, mais pas localement connexe. En mathématiques, plus précisément en topologie, un espace localement connexe est … Wikipédia en Français
Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… … Wikipédia en Français
Espace localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Espace simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Localement compact — Espace localement compact En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de… … Wikipédia en Français
Connexité par arcs — En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En… … Wikipédia en Français
Espace semi-localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Localement simplement connexe — Connexité simple En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement « d un seul tenant », un espace simplement connexe est de plus sans « trou » ni… … Wikipédia en Français
Espace connexe — Connexité (mathématiques) Pour les articles homonymes, voir Connexité. Un archipel, comme celui des îles Canaries, n est pas connexe : il n est pas possible de passer à pied sec d une île à l autre. Les îles sont les composantes connexes … Wikipédia en Français
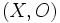 un espace topologique. On dit que
un espace topologique. On dit que 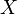 est localement connexe par arcs si tout voisinage de tout point
est localement connexe par arcs si tout voisinage de tout point  de
de 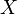 contient un voisinage connexe par arcs de
contient un voisinage connexe par arcs de  (pour la topologie induite par la topologie de
(pour la topologie induite par la topologie de 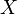 ).
).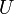 , les composantes connexes par arcs de
, les composantes connexes par arcs de 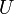 sont ouvertes.
sont ouvertes.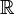 ,
, 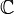 ,
, 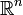 ...
...