Description Lagrangienne

Description Lagrangienne

Description lagrangienne

Pour décrire mathématiquement les propriétés d'un fluide en mouvement, deux systèmes cohabitent, l'un et l'autre présentant des avantages dans des situations particulières. Il s'agit de la description lagrangienne et de la description eulérienne.

La description lagrangienne consiste à observer les modifications des propriétés d'une particule fluide que l'on suit dans son mouvement.

Dans le cadre de cette description, et ρ désignant la densité du fluide, 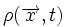\rho(\overrightarrow{x},t) désigne la densité du fluide qui, initialement (temps 0), était à la position 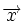\overrightarrow{x} et se trouve désormais (temps t) en 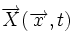\overrightarrow{X}(\overrightarrow{x},t)... mais cela peut bien sûr s'appliquer à n'importe quelle autre fonction décrivant une propriété locale du fluide.

Cette description donne une bonne idée de ce qui se passe dans le fluide, par exemple, si 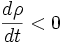\frac{d\rho}{dt}<0, alors on peut affirmer que le fluide s'étend (la densité de la particule fluide baisse). La dérivée droite 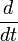\frac{d}{dt} est réservée à la description lagrangienne. 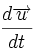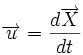En particulier, on peut faire un bilan des forces s'appliquant à la particule fluide que l'on suit, et appliquer la relation fondamentale de la dynamique en écrivant que la somme des forces vaut la masse de la particule fluide multipliée par son accélération, écrite comme \frac{d\overrightarrow{u}}{dt} où \overrightarrow{u} = \frac{d\overrightarrow{X}}{dt} est la vitesse.

L'inconvénient de cette méthode est que le référentiel se déplace avec le fluide, et donc, qu'il est difficile de connaître l'état du fluide en un point donné de l'espace et du temps.


Le lien entre la description lagrangienne et la description eulérienne est démontré ici en 1D : Pendant l'intervalle de temps dt, une particule fluide s'est déplacée de (x,t) à (x+vdt,t+dt), donc on peut écrire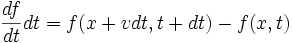

\frac{df}{dt} dt = f(x+vdt,t+dt)-f(x,t)

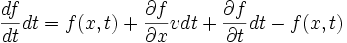
\frac{df}{dt} dt = f(x,t)+\frac{\partial f}{\partial x} v dt + \frac{\partial f}{\partial t} dt -f(x,t)

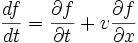
\frac{df}{dt} = \frac{\partial f}{\partial t} + v \frac{\partial f}{\partial x}

... que l'on généralise en 3D à :

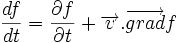
\frac{df}{dt} = \frac{\partial f}{\partial t} + \overrightarrow{v}.\overrightarrow{grad} f

  • Portail de la physique Portail de la physique
Ce document provient de « Description lagrangienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Description Lagrangienne de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Description lagrangienne — Pour les articles homonymes, voir Description (Homonymie) et lagrangien (homonymie). En dynamique des fluides la description lagrangienne est l une des deux techniques qui permettent de caractériser un écoulement. Elle consiste à suivre dans le… …   Wikipédia en Français

  • Description Eulérienne — Pour décrire mathématiquement les propriétés d un fluide en mouvement, deux systèmes cohabitent, l un et l autre présentant des avantages dans des situations particulières. Il s agit de la description lagrangienne et de la description eulérienne …   Wikipédia en Français

  • Description eulerienne — Description eulérienne Pour décrire mathématiquement les propriétés d un fluide en mouvement, deux systèmes cohabitent, l un et l autre présentant des avantages dans des situations particulières. Il s agit de la description lagrangienne et de la… …   Wikipédia en Français

  • Description (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « description », sur le Wiktionnaire (dictionnaire universel) Le mot description entre dans le titre de… …   Wikipédia en Français

  • Description eulérienne — Pour les articles homonymes, voir Description (Homonymie). En dynamique des fluides la description eulérienne est l une des deux techniques qui permettent de caractériser un écoulement. Elle décrit le champ de vitesses qui associe à chaque point… …   Wikipédia en Français

  • DESCRIPTION ET EXPLICATION — Certaines disciplines sont descriptives: astronomie, anatomie, zoologie. Une description peut être plus qu’une simple collection non ordonnée de faits ou de données, l’exemple des taxinomies le montre. La géographie comporte une partie… …   Encyclopédie Universelle

  • Dérivation lagrangienne — Concepts de base en théorie des milieux continus Cet article traite des concepts de base en théorie des milieux continus. De nombreux articles de Wikipédia traitent de milieux continus dans le cadre de différents domaines de la physique :… …   Wikipédia en Français

  • Relaxation lagrangienne — La relaxation lagrangienne est une technique de relaxation qui consiste à supprimer des contraintes difficiles en les intégrant dans la fonction objectif en la pénalisant si cette contrainte n est pas respectée. Description Mathématique Étant… …   Wikipédia en Français

  • Concepts De Base En Théorie Des Milieux Continus — Cet article traite des concepts de base en théorie des milieux continus. De nombreux articles de Wikipédia traitent de milieux continus dans le cadre de différents domaines de la physique : mécanique, hydrodynamique, élasticité, rhéologie,… …   Wikipédia en Français

  • Concepts de base en theorie des milieux continus — Concepts de base en théorie des milieux continus Cet article traite des concepts de base en théorie des milieux continus. De nombreux articles de Wikipédia traitent de milieux continus dans le cadre de différents domaines de la physique :… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”