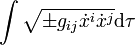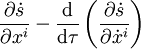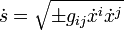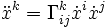Équation géodésique
- Équation géodésique
-
Équation des géodésiques
On obtient l'équation d'une géodésique en exprimant que sa longueur est minimale – par définition.
Un système de coordonnées xi étant donné, le tenseur métrique donne la longueur d'une courbe infinitésimale
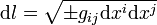 .
.
Le signe optionnel 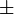 est choisi en fonction du signe de l'intervalle et de la signature du tenseur métrique.
est choisi en fonction du signe de l'intervalle et de la signature du tenseur métrique.
Si la courbe est paramétrée au moyen d'une variable τ, on écrit
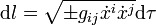 ,
,
où le point supérieur représente la dérivée totale par rapport à τ. La longueur de la trajectoire est donc la somme
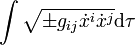
En utilisant la méthode de Lagrange pour exprimer que l'intégrale est minimale, on obtient l'équation géodésique
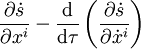
avec
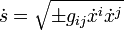
La paramétrisation canonique τ = s des trajectoires permet d'obtenir une équation mettant en jeu le symbole de Christoffel (voir Équation géodésique et symbole de Christoffel) :
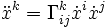
Voir aussi
 Portail des mathématiques
Portail des mathématiques Portail de la physique
Portail de la physique
Catégories : Calcul tensoriel | Géodésie | Relativité générale | Géométrie riemannienne
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Équation géodésique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Equation geodesique et symbole de Christoffel — Équation géodésique et symbole de Christoffel Un système de coordonnées étant donné, si l on choisit de paramétrer les courbes par la mesure de leur longueur (appelé paramètre canonique), l équation des géodésiques devient où Γkij est un symbole… … Wikipédia en Français
Équation géodésique et symbole de christoffel — Un système de coordonnées étant donné, si l on choisit de paramétrer les courbes par la mesure de leur longueur (appelé paramètre canonique), l équation des géodésiques devient où Γkij est un symbole de Christoffel. Le point supérieur est la… … Wikipédia en Français
Équation géodésique et symbole de Christoffel — Un système de coordonnées étant donné, si l on choisit de paramétrer les courbes par la mesure de leur longueur (appelé paramètre canonique), l équation des géodésiques devient où Γkij est un symbole de Christoffel. Le point supérieur est la… … Wikipédia en Français
Geodesique — Géodésique En géométrie, une géodésique désigne le chemin le plus court, ou l un des plus courts chemins s il en existe plusieurs, entre deux points d un espace pourvu d une métrique (un moyen de mesurer les distances). Lorsque l on change cette… … Wikipédia en Français
Equation des geodesiques — Équation des géodésiques On obtient l équation d une géodésique en exprimant que sa longueur est minimale – par définition. Un système de coordonnées xi étant donné, le tenseur métrique donne la longueur d une courbe infinitésimale . Le signe… … Wikipédia en Français
Géodésique — En géométrie, une géodésique désigne le chemin le plus court, ou l un des plus courts chemins s il en existe plusieurs, entre deux points d un espace pourvu d une métrique (un moyen de mesurer les distances). Lorsque l on change cette notion de… … Wikipédia en Français
Équation des géodésiques — On obtient l équation d une géodésique en exprimant que sa longueur est minimale – par définition. Un système de coordonnées xi étant donné, le tenseur métrique donne la longueur d une courbe infinitésimale . Le signe optionnel est choisi en… … Wikipédia en Français
Equation d'Einstein — Équation d Einstein L équation d Einstein ou équation de champ d Einstein est l équation aux dérivées partielles principale de la relativité générale. C est une équation dynamique qui décrit comment la matière et l énergie modifient la géométrie… … Wikipédia en Français
Équation de champ — Équation d Einstein L équation d Einstein ou équation de champ d Einstein est l équation aux dérivées partielles principale de la relativité générale. C est une équation dynamique qui décrit comment la matière et l énergie modifient la géométrie… … Wikipédia en Français
Équation de champ d'Einstein — Équation d Einstein L équation d Einstein ou équation de champ d Einstein est l équation aux dérivées partielles principale de la relativité générale. C est une équation dynamique qui décrit comment la matière et l énergie modifient la géométrie… … Wikipédia en Français
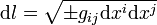 .
.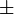 est choisi en fonction du signe de l'intervalle et de la signature du tenseur métrique.
est choisi en fonction du signe de l'intervalle et de la signature du tenseur métrique.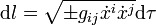 ,
,