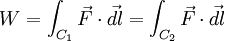Force non conservative

Force conservative

Une force est dite conservative lorsque le travail produit par cette force est indépendant du chemin suivi par son point d'action. Si ce n'est pas le cas elle alors dite non-conservative.

Ce type de force possède trois propriétés remarquables :

L'énergie mécanique d'un système soumis uniquement à l'action de forces conservatives est conservée.
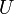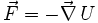Il existe un champ scalaire $U\,$ , aussi appelé potentiel, tel que la force s'écrit $\vec{F}=-\vec{\nabla}\,U\,$ .
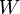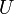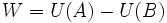Si le point d'application d'une force conservative se déplace d'un point A à un point B, le travail $W\,$ de la force en question s'obtient simplement à partir du potentiel $U\,$ : $W=U(A)-U(B)\,$ .

Sommaire

1 Exemples courants de forces conservatives et non-conservatives
2 Indépendance du chemin suivi
3 Potentiel d'une force conservative
- 3.1 Existence du potentiel
- 3.2 Réciproque
4 Conservation de l'énergie mécanique
5 Notes
6 Voir aussi

Exemples courants de forces conservatives et non-conservatives

Conservatives :

La force électrique qui dérive du potentiel électrique.
La force gravitationnelle qui dérive du potentiel de gravitation.

Non-conservatives :

La force de Lorentz^[1] ne travaillant pas mais ne dérivant pas d'un potentiel, on ne les place donc pas dans la catégorie des forces conservatives.
Les forces de frottement, qu'il s'agisse de frottement solide ou de frottement fluide ne sont pas des forces conservatives car leur travail dépend explicitement du chemin suivi par le système.
Les forces de pression ne sont pas conservatives car au cours de l'évolution, de l'énergie est transmise à l'environnement extérieur au système.

Indépendance du chemin suivi

Considérons une particule matérielle se déplaçant d'un point A vers un point B, et sur lequel s'exerce une force 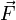$\vec{F}$ conservative, alors le travail produit par cette force ne dépend pas du chemin suivi par le solide. Ainsi pour deux trajectoires C₁ et C₂ reliant le point A au point B, la force fournit le même travail :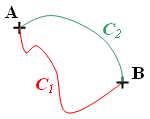

Chemins d intégration.png

$W=\int_{C_1}\vec{F}\cdot\vec{dl}=\int_{C_2}\vec{F}\cdot\vec{dl}$

Une conséquence immédiate de cette propriété est que dans le cas d'une trajectoire fermée (si la particule retourne à sa position initiale), le travail d'une force conservative est nul.

Potentiel d'une force conservative

Existence du potentiel

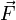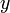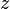Considérons maintenant une force conservative fonction de la position de son point d'application, c'est-à-dire telle que $\vec{F}$ soit une fonction des coordonnées $x\,$ , $y\,$ et $z\,$ alors, en vertu de l'indépendance du chemin suivi, quelle que soit la trajectoire fermée 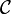$\mathcal{C}\,$ , le travail de la force est nul :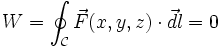

$W=\oint_{\mathcal{C}}\vec{F}(x,y,z)\cdot\vec{dl}=0$

dont on déduit d'après le théorème de Stokes que 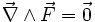$\vec{\nabla}\wedge\vec{F}=\vec{0}$ . Cette dernière relation implique l'existence d'un champ scalaire 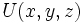$U(x,y,z)\,$ tel que :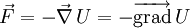

$\vec{F}=-\vec{\nabla}\,U=-\overrightarrow{\mathrm{grad}}\,U$

Le champ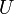 $U\,$ est appelé potentiel de la force et est homogène à une énergie. De par sa définition, le champ 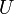$U\,$ est défini à une constante près. La valeur de cette dernière est généralement arbitraire, auquel cas elle est choisie de façon à simplifier les calculs.

Réciproque

Réciproquement, considérons une force 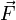$\vec{F}$ dérivant d'un potentiel $U\,$ :

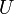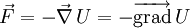
$\vec{F}=-\vec{\nabla}\,U=-\overrightarrow{\mathrm{grad}}\,U$

En remarquant que 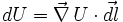$dU=\vec{\nabla}\,U\cdot\vec{dl}$ est une différentielle totale, on trouve que le travail de la force prend l'expression suivante :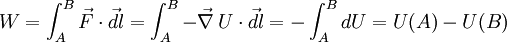

$W=\int_{A}^{B}\vec{F}\cdot\vec{dl}=\int_{A}^{B}-\vec{\nabla}\,U\cdot\vec{dl} =-\int_{A}^{B}dU=U(A)-U(B)$

Le travail ne dépend donc que de la valeur du potentiel aux points A et B. Le travail d'une force dérivant d'un potentiel ne dépend donc pas du chemin suivi, une telle force est donc conservative.

Conservation de l'énergie mécanique

Les forces conservatives sont appelées ainsi parce l'énergie mécanique d'un système soumis à l'action de forces conservatives est constante : l'énergie du système se conserve.

Cette propriété est une conséquence immédiate du théorème de l'énergie cinétique. Pour un solide parcourant une trajectoire reliant un point A à un point B et soumis à une force conservative de potentiel 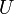$U\,$ , on a d'une part égalité entre la variation de l'énergie cinétique et le travail de la force :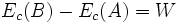

$E_c(B)-E_c(A)=W\,$

et d'autre part, le travail de la force conservative qui s'obtient à partir de la variation du potentiel entre les points A et B :

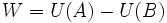
$W=U(A)-U(B)\,$

dont on déduit immédiatement l'égalité suivante :

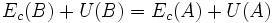
$E_c(B) + U(B)=E_c(A) + U(A)\,$

On voit donc que la somme de l'énergie cinétique et du potentiel se conserve. Cette quantité est précisément l'énergie mécanique du système. L'expression ci-dessus montre clairement que l'énergie totale se répartit entre l'énergie cinétique et le potentiel, et peut donc passer successivement de l'une à l'autre. C'est pourquoi le potentiel 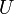$U\,$ est aussi appelé énergie potentielle : c'est de l'énergie qui peut potentiellement se transformer en énergie cinétique.

Notes

↑ Ainsi que son cas particulier, la force de Laplace agissant sur un élément de circuit électrique

Voir aussi

Portail de la physique

Ce document provient de « Force conservative ».

Catégorie : Mécanique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Force non conservative de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

force non-conservative — nekonservatyvioji jėga statusas T sritis fizika atitikmenys: angl. non conservative force vok. nichtkonservative Kraft, f rus. неконсервативная сила, f pranc. force non conservative, f … Fizikos terminų žodynas
non-conservative force — nekonservatyvioji jėga statusas T sritis fizika atitikmenys: angl. non conservative force vok. nichtkonservative Kraft, f rus. неконсервативная сила, f pranc. force non conservative, f … Fizikos terminų žodynas
Force Conservative — Une force est dite conservative lorsque le travail produit par cette force est indépendant du chemin suivi par son point d action. Si ce n est pas le cas elle alors dite non conservative. Ce type de force possède trois propriétés… … Wikipédia en Français
Force — For other uses, see Force (disambiguation). See also: Forcing (disambiguation) Forces are also described as a push or pull on an object. They can be due to phenomena such as gravity, magnetism, or anything that might cause a mass to accelerate … Wikipedia
Conservative force — Classical mechanics Newton s Second Law History of classical mechanics … Wikipedia
Force conservative — Une force est dite conservative lorsque le travail produit par cette force est indépendant du chemin suivi par son point d action. Si ce n est pas le cas elle est alors dite non conservative. Ce type de force possède trois propriétés… … Wikipédia en Français
Force centrale, mouvement — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Conservative Halakha — Part of a series of articles on Jews and Judaism … Wikipedia
Conservative Party (UK) — Conservative Party Conservative and Unionist Party Leader … Wikipedia
CONSERVATIVE JUDAISM — (also known as Masorti Judaism), one of the three principal modern Jewish religious denominations, emerging, along with Reform and Orthodoxy, in the 19th century era of emancipation. After the denial of emancipation to Central European Jewry by… … Encyclopedia of Judaism

Dictionnaires et Encyclopédies sur 'Academic'

Force non conservative

Force conservative

Sommaire

Exemples courants de forces conservatives et non-conservatives

Indépendance du chemin suivi