- Visqueux
-
Viscosité
La viscosité (du latin viscum) peut être definie comme étant la résistance à l'écoulement uniforme et sans turbulence se produisant dans la masse d'une matière. La viscosité dynamique représente la contrainte de cisaillement nécessaire pour produire un gradient de vitesse d'écoulement d'une unité dans la matière. Nem
Lorsque la viscosité augmente, la capacité du fluide à s'écouler diminue. Pour un liquide, la viscosité tend généralement à diminuer lorsque la température augmente. On pourrait croire que la viscosité d'un fluide s'accroît avec sa densité mais ce n'est pas nécessairement le cas: l'huile est moins dense que l'eau (huile de colza: 0.92 à 20°C, contre 1 pour l'eau) cependant elle est nettement plus visqueuse.
On classe notamment les huiles mécaniques selon leur viscosité, en fonction des besoins de lubrification du moteur et des températures auxquelles l'huile sera soumise lors du fonctionnement du moteur. [1]
Sommaire
Grandeurs physiques
Plusieurs grandeurs physiques sont reliées à la viscosité.
La viscosité dynamique
La viscosité dynamique μ (ou encore η) se mesure en pascal-seconde (Pa.s), cette unité ayant remplacé le poiseuille (Pl) qui a la même valeur. On trouve encore parfois l'ancienne unité du système CGS, la poise (Po) : 1 Pa.s = 10 Po.
La viscosité de l'eau à 20°C est de 1 cPo (centipoise) soit 10^(-3) Pa.s
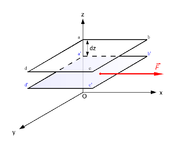
Une façon de définir la viscosité dynamique est de considérer deux couches d'un fluide notées abcd et a’b'c'd', la couche abcd étant animée d'une vitesse relative à a'b'c'd' notée dv et dirigée suivant x. Sous l'effet de la viscosité, une force F s'exerce sur la couche a'b'c'd'. La viscosité dynamique μ est définie par la relation entre la norme de cette force et la vitesse relative dv
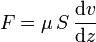 ,
,S étant la surface de chaque couche, et dz l'épaisseur de fluide séparant les deux couches.
La viscosité cinématique
Article détaillé : viscosité cinématique.La viscosité cinématique ν (nu) s'obtient en divisant la viscosité dynamique par la masse volumique ρ soit
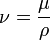 .
.Elle s'exprime en m²/s. Dans le système CGS la viscosité cinématique était exprimée en stokes (St) ou en centistokes (cSt).
La conversion est immédiate, puisque 1 St = 1 cm²/s = 10-4 m²/s et 1 cSt = 1 mm²/s = 10-6 m²/s.
La fluidité
La fluidité est l'inverse de la viscosité dynamique.
Évolution suivant la température
La viscosité d'un fluide varie en fonction de sa température ou des actions mécaniques auxquelles il est soumis. Voir par exemple à ce propos le phénomène de thixotropie. Pour déterminer l'importance de la température sur la viscosité d'un fluide on utilise un indice de viscosité. Plus cet indice est grand, moins la température a d'influence sur la viscosité du fluide.
Concernant un gaz, il est courant d'utiliser la loi de Sutherland définie de la façon suivante :
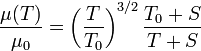
μ0 = μ(T0) est la viscosité à la température T0, S est la température de Sutherland. Pour l'air par exemple on prend habituellement les valeurs suivantes μ0 = 1,711⋅10-5 Pl, T0 = 273,15 K et S = 110,4 K, ce qui donne une bonne approximation sur une plage de température de l'ordre de 170 K à 1900 K environ.
Quelques valeurs
viscosité dynamique corps température (°C) viscosité (Pa s) Fluide parfaitement défini hydrogène 0 8,4 × 10-6 50 9,3 × 10-6 100 10,3 × 10-6 air 0 17,1 × 10-6 50 19,4 × 10-6 100 22,0 × 10-6 xénon 0 21,2 × 10-6 eau 0 1,793 × 10-3 20 1,002 × 10-3 50 0,5470 × 10-3 100 0,2818 × 10-3 glace -13 15 × 1012 mercure 20 1,554 acétone 0,326 × 10-3 éthanol 1,20 × 10-3 méthanol 0,59 × 10-3 benzène 0,64 × 10-3 nitrobenzène 2,0 × 10-3 glycérine 1,49 Fluide de la vie courante bitume 20 108 mélasse 20 102 miel 20 101 huile de ricin 20 3,4 huile d'olive 20 [81 × 10-2...100 * 10-2] café crème 20 10 × 10-3 sang 37 [4 × 10-3...25 × 10-3] jus de raisin 20 [2 × 10-3...5 × 10-3] pétrole 20 0,65 × 10-3 Viscosité de corps à la pression atmosphérique viscosité cinématique corps température (°C) viscosité (cst) Huile 40 20 à 60[2] Voir aussi
Liens externes
Références
- Portail de la physique
Catégories : Mécanique des fluides | Rhéologie | Grandeur physique
Wikimedia Foundation. 2010.