Theorie des noeuds

Theorie des noeuds

Théorie des nœuds

Page d'aide sur l'homonymie Pour les articles homonymes, voir nœud.
illustration de la théorie des nœuds

La théorie des nœuds est une branche de la topologie qui consiste en l'étude mathématique de bouts de ficelles idéalisés. La théorie des nœuds est donc très proche de la théorie des tresses.

Sommaire

Histoire

Nœuds triviaux

La théorie des nœuds a une longue histoire. On peut peut-être la faire commencer avec des travaux de Gauss liés à l'électromagnétisme.

Les nœuds furent étudiés par Carl Friedrich Gauss qui a introduit une formule intégrale calculant le « nombre de liaison » entre deux nœuds. Son étudiant Johann Benedict Listing a poursuivi leur étude. La première étude poussée est survenue plus tard, lorsque William Thomson (Lord Kelvin) proposa une théorie des atomes vortex.

En 1867, après avoir pris connaissance des expériences du physicien écossais Peter Guthrie Tait sur les anneaux de fumée, Thomson eut l'idée que les atomes pouvaient être des nœuds formés dans l'éther. Les éléments chimiques correspondraient alors aux nœuds et aux entrelacs. Les experiences de Tait étaient inspirées par un article de Helmholtz sur les anneaux-vortex dans les fluides incompressibles. Thomson et Tait pensaient qu'une compréhension et une classification des nœuds expliquerait pourquoi les atomes absorbent et émettent de la lumière seulement pour certaines longueurs d'onde. Ainsi, Thomson pensait que le sodium pouvait correspondre à l'entrelac de Hopf, à cause de ses deux lignes spectrales.

Tait entreprit alors de compiler une table des nœuds, dans l'espoir d'obtenir ainsi une table des éléments chimiques. Il formula alors les conjectures de Tait sur les nœuds alternés, qui ne furent démontrées que dans les années 1990. Les tables de Tait furent par la suite améliorées par C. N. Little et T. P. Kirkman.

James Clerk Maxwell, collègue et ami de Thomson et Tait, s'est aussi beaucoup intéressé aux nœuds. Maxwell a étudié le travail de Listing sur le sujet. Il a réinterprété l'intégrale de liaison de Gauss en termes de sa propre théorie de l'électromagnétisme. Dans cette formulation, l'intégrale représente le travail accompli par une particule se déplaçant le long d'une composante sous l'influence du champ magnétique crée par un courant parcourant l'autre composante. Maxwell a aussi poursuivi l'étude des anneaux de fumée en considérant le cas de trois anneaux en interaction.

Quand l'expérience de Michelson-Morley a montré que l'éther n'existait pas, la théorie des atomes vortex est tombée en désuétude. La physique moderne explique le spectre discret d'absorption et d'émission des atomes par leur niveaux d'énergie quantifiés.

Aujourd'hui, la théorie des nœuds est étudiée principalement pour ses liens avec la topologie et les systèmes dynamiques[1] et possède de nombreuses applications en mathématiques et en physique théorique.

Cadre mathématique

Plus formellement, on considère les plongements du cercle 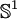\mathbb{S}^1 dans l'espace euclidien 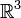\mathbb{R}^3 de dimension 3. Un nœud est un tel plongement considéré à déformation (ou isotopie) près. Il s'agit donc plutôt ici de ficelles sans bouts (une erse aux sens des boscos) que de nœuds au sens habituel.

Equivalence de nœuds

Le problème principal est de déterminer si deux plongements différents sont en fait le même nœud. Pour cela, il convient de construire des invariants des nœuds, qui sont des fonctions sur l'ensemble des plongements qui ne dépendent que du nœud. Une fois défini un invariant, il faudra encore chercher à savoir dans quelle mesure il prend des valeurs différentes sur des nœuds différents.

Invariants de nœuds

Parmi les principaux invariants des nœuds, citons le polynôme de Jones, le polynôme d'Alexander, le polynôme HOMFLY, le groupe fondamental du complémentaire du nœud, les invariants de type fini de Vassiliev et l'intégrale de Kontsevich.

Parmi les derniers invariants introduits, il y a notamment des groupes d'homologie de nœuds définis par Khovanov.

  1. ↑ Voir en particulier un exposé d'Étienne Ghys et son support.

Bibliographie

Alexei Sossinsky - Nœuds, Genèse d'une théorie mathématique, éditions du Seuil, Paris (1999) ISBN 2-02-032089-4

Voir aussi

Liens externes

Valknop platt.jpg

Commons-logo.svg
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9orie des n%C5%93uds ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theorie des noeuds de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Théorie des noeuds — Théorie des nœuds Pour les articles homonymes, voir nœud. La théorie des nœuds est une branche de la topologie qui consiste en l étude mathématique de bouts de ficelles idéalisés. La théorie des nœuds est donc très proche de la théorie des… …   Wikipédia en Français

  • Theorie des tresses — Théorie des tresses La théorie des tresses est l étude des tresses, objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Loin d être une simple distraction mathématique, les tresses ont une structure de groupe… …   Wikipédia en Français

  • Théorie des tresses — La théorie des tresses est l étude des tresses, objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Loin d être une simple distraction mathématique, les tresses ont une structure de groupe naturelle, et… …   Wikipédia en Français

  • Théorie des nœuds — Pour les articles homonymes, voir nœud. illustration de la théorie des nœuds La théorie des nœuds est une branche de la topologie qui consiste e …   Wikipédia en Français

  • Loi des noeuds — Lois de Kirchhoff Portrait de Gustav Robert Kirchhoff, qui a établi les lois portant son nom en 1845. Les lois de Kirchhoff expriment la conservation de l énergie et de la charge dans un circuit électrique. Elles portent le nom du physicien… …   Wikipédia en Français

  • Noeuds — Nœud Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Méthode des nœuds — Dans un noeud, la somme des courants entrants égale la somme des courants sortants. La méthode des nœuds est la mise en pratique d une des lois de Kirchhoff : la loi des noeuds (circuits). Il s agit de poser le système d équations où les… …   Wikipédia en Français

  • Groupe de tresses — Théorie des tresses La théorie des tresses est l étude des tresses, objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Loin d être une simple distraction mathématique, les tresses ont une structure de groupe… …   Wikipédia en Français

  • Forme de contact — Géométrie de contact Structure standard sur ℝ3 : champ de plans La géométrie de contact est la partie de la géométrie différentielle qui étudie les formes et structures de contact. Elle entretient d étroits liens avec la géométrie… …   Wikipédia en Français

  • Geometrie de contact — Géométrie de contact Structure standard sur ℝ3 : champ de plans La géométrie de contact est la partie de la géométrie différentielle qui étudie les formes et structures de contact. Elle entretient d étroits liens avec la géométrie… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”