- Diagramme De Lien
-
Diagramme de lien
 Pour les articles homonymes, voir Lien.
Pour les articles homonymes, voir Lien.Un lien, ou entrelacs, en topologie est un ensemble de courbes de l'espace, fermées et d'intersection vide deux à deux. La théorie des nœuds étudie les configurations possibles de ces objets. (Un nœud est un lien ne possédant qu'une seule courbe.) Un diagramme de lien est une représentation bidimensionelle d'un lien.
Projection du lien
Pour obtenir un diagramme de lien à partir du lien, on le projette sur un plan. Lorsqu'un croisement se produit, on garde en mémoire la position relative d'un segment par rapport à l'autre (en «hauteur») en coupant légèrement le segment du dessous autour de celui du dessus comme sur la figure :
Cependant on doit respecter certaines règles pour projeter le lien.
- Les courbes doivent être lisses, sans point singulier.
- Deux portions de courbes ne doivent pas être tangentes.
- Les croisements doivent toujours n'impliquer que deux portions de courbes.
Ces règles sont en réalité peu contraignantes, car une légère modification de la direction de projection permet de se débarrasser de tous les cas.
Liens et graphesSi on donne un numérote les portions de courbes, comme chaque croisement est en contact avec trois portions de courbes on définit une structure de graphe pour le diagramme dont tous les sommets sont d'ordre 4. (Si un croisement est constitué de moins de trois portions de courbes, on a une boucle qui ne joue pas de rôle dans la structure du graphe.)
Relations entre les diagrammes
On peut avoir différentes projections du même objet, par exemple en changeant de direction d'observation. Cependant il existe un moyen de relier des diagrammes entre eux.
Mouvements de Reidemeister 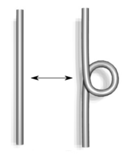
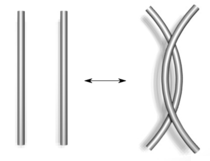
Type I Type II 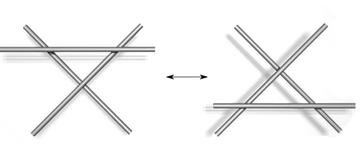
Type III Si on veut relier deux diagrammes qui sont la projection d'un même lien ou de ses déformations sans couper aucune courbe, on utilise les relations de Reidemeister. Ces relations sont une conséquence des règles de projection. Elles relient entre elles les différentes situations que l'on obtient en le résolvant (en changeant légèrement de direction de projection).
- Portail des mathématiques
Catégories : Théorie des nœuds | Diagramme
Wikimedia Foundation. 2010.

