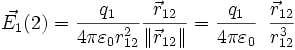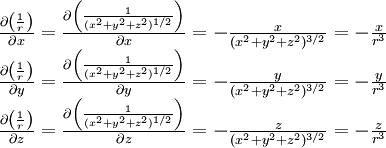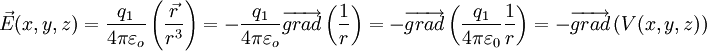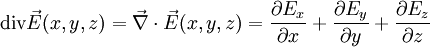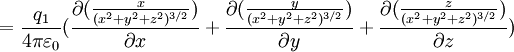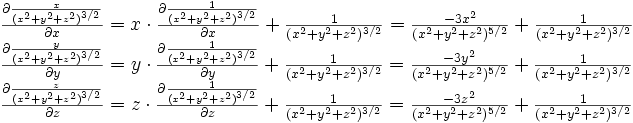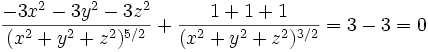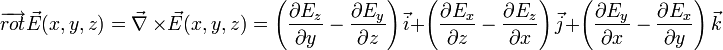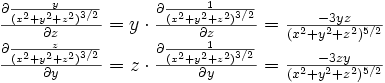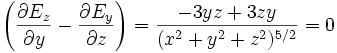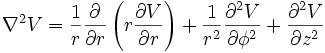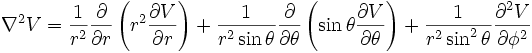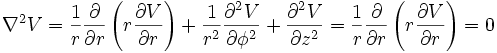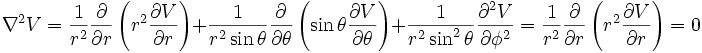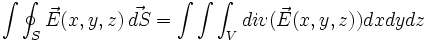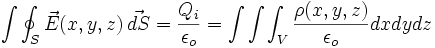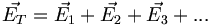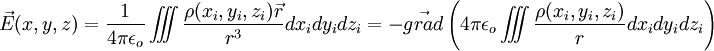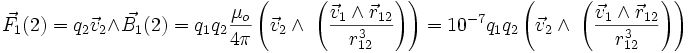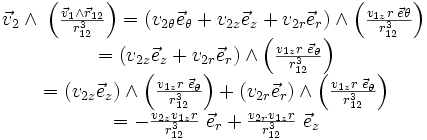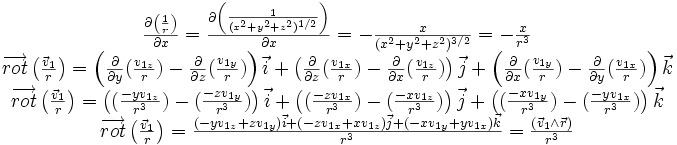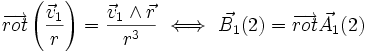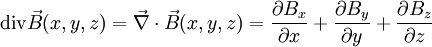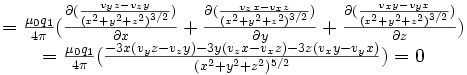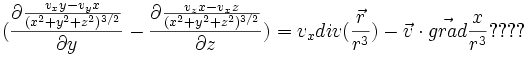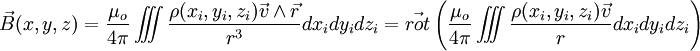Electrostatique magnetostatique (formulaire)

Électrostatique magnétostatique (formulaire)

Cet article fait partie de la série
formulaire de physique

Optique

Électro- Magnéstatique

Physique quantique

Thermodynamique

Mécanique des fluides

Mécanique

Relativité restreinte

Trou noir

Analyse vectorielle

Sommaire

1 Electrostatique
2 Magnétostatique

Electrostatique

Force électrostatique

La force électrostatique entre deux charges ponctuelles ( $q 1, q 2$ ) est donnée par la loi de Coulomb :

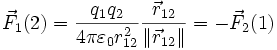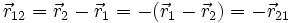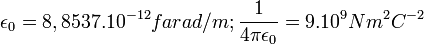
$\vec{F}_1(2) = \frac{q_1 q_2}{4 \pi \varepsilon_0 r_{12}^2}\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|}=-\vec{F}_2(1)$ avec $\vec{r}_{12}=\vec{r}_2- \vec{r}_1 =-(\vec{r}_1- \vec{r}_2)=-\vec{r}_{21}$ et $\epsilon_0 = 8,8537.10^{-12}farad/m ; \frac{1}{4 \pi \epsilon_0}=9.10^9 N m^2C^{-2}$

Deux charges de 1 coulomb situées à 1 mètre l'une de l'autre se repoussent avec une force de $9.10 9 N$ et cette force maintiendrait en lévitation quasiment un million de tonnes ! Alors que un courant de 1 ampère correspond au passage de 1 coulomb par seconde. Le coulomb est adapté lorsque l'on parle de courant électrique et d'énergie électrique: 1 watt = 1 coulomb x 1 volt Un électron a une charge de $1,6.10 - 19 C$ et les énergies le concernant s'expriment en 1 électron x 1 volt = 1eV

Champ électrostatique

Le champ électrostatique créé en 2 par une charge ponctuelle $q 1$ située en 1 (la charge pouvant être positive ou négative) vaut, en unités SI :

$\vec{E_1}(2) = \frac{q_1}{4 \pi \varepsilon_0 r_{12}^2}\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|}= \frac{q_1}{4 \pi \varepsilon_0 }\;\;\frac{\vec{r}_{12}} {r_{12}^3}$

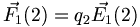
La force s'exerçant sur une charge $q 2$ plongée dans ce champ au point 2 vaut alors : $\vec{F_1}(2) = q_2 \vec{E_1}(2)$

Champ gradient d'un potentiel

Avec $\vec{r}_{1}=\vec{0} \ et\ \vec{r}_2 = \vec{r}$ C'est à dire en plaçant l'origine sur la charge pour simplifier les écritures et les calculs, et en remarquant que le calcul mathématique des dérivées partielles donne pour r non nul:

$\begin{matrix} \\ \frac {\partial \left( \frac{1}{r} \right)} {\partial x}= \frac {\partial \left( \frac{1}{(x^2+y^2+z^2)^{1/2}} \right)} {\partial x}= - \frac {x}{(x^2+y^2+z^2)^{3/2}}= - \frac {x}{r^3 } \\ \frac {\partial \left( \frac{1}{r} \right)} {\partial y}=\frac {\partial \left( \frac{1}{(x^2+y^2+z^2)^{1/2}} \right)} {\partial y}= - \frac {y}{(x^2+y^2+z^2)^{3/2}}=- \frac {y}{r^3} \\ \frac {\partial \left( \frac{1}{r} \right)} {\partial z}=\frac {\partial \left( \frac{1}{(x^2+y^2+z^2)^{1/2}} \right)} {\partial z}= - \frac {z}{(x^2+y^2+z^2)^{3/2}}=- \frac {z}{r^3 } \\\end{matrix}$

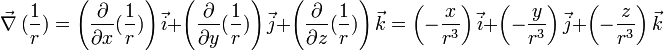
soit : $\vec \nabla \ (\frac {1}{r})= \left(\frac {\partial } {\partial x}(\frac {1}{r})\right) \vec {i}+ \left(\frac {\partial } {\partial y}(\frac {1}{r})\right) \vec {j}+\left(\frac {\partial } {\partial z}(\frac {1}{r})\right) \vec {k} =\left(- \frac {x}{r^3 } \right) \vec {i}+ \left(- \frac {y}{r^3 } \right) \vec {j}+\left(- \frac {z}{r^3 } \right) \vec {k}$

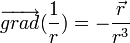
finalement : $\overrightarrow {grad} ( \frac {1}{r}) =- \frac{\vec r}{r^3}$

Ce résultat est une égalité purement mathématique et on obtient l'expression correspondante de la physique en simplement multipliant 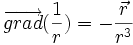$\overrightarrow {grad} ( \frac {1}{r}) =- \frac{\vec r}{r^3}$ par la constante physique : 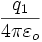$\frac{q_1}{4 \pi \varepsilon_o}$ pour une charge q1 ponctuelle :

$\vec {E}(x, y, z) = \frac{q_1}{4 \pi \varepsilon_o} \left(\frac{\vec r}{r^3} \right) = - \frac{q_1}{4 \pi \varepsilon_o} \overrightarrow {grad} \left( \frac{1}{r}\right)= - \overrightarrow {grad} \left( \frac{q_1}{4 \pi \varepsilon_0}\frac{1}{r}\right)= - \overrightarrow {grad} \left( V(x, y, z) \right)$

Tout ceci étant linéaire, c'est encore vérifié pour une distribution quelconque de charges.

Champ à divergence nulle

$\mathrm{div} \vec {E}(x, y, z) = \vec \nabla \cdot \vec{E}(x, y, z) = \frac {\partial E_x} {\partial x} + \frac {\partial E_y} {\partial y} + \frac {\partial E_z} {\partial z}$

$= \frac{q_1}{4 \pi \varepsilon_0}(\frac {\partial (\frac{x}{(x^2+y^2+z^2)^{3/2}})} {\partial x} + \frac {\partial (\frac{y}{(x^2+y^2+z^2)^{3/2}})} {\partial y} + \frac {\partial (\frac{z}{(x^2+y^2+z^2)^{3/2}})} {\partial z})$

Or :

$\begin{matrix} \\ \frac {\partial \frac{x}{(x^2+y^2+z^2)^{3/2}}} {\partial x}= x\cdot\frac {\partial \frac{1}{(x^2+y^2+z^2)^{3/2}}}{\partial x} + \frac{1}{(x^2+y^2+z^2)^{3/2}} = \frac{-3x^2}{(x^2+y^2+z^2)^{5/2}} + \frac{1}{(x^2+y^2+z^2)^{3/2}} \\ \frac {\partial \frac{y}{(x^2+y^2+z^2)^{3/2}}} {\partial y}= y\cdot\frac {\partial \frac{1}{(x^2+y^2+z^2)^{3/2}}}{\partial y} + \frac{1}{(x^2+y^2+z^2)^{3/2}} = \frac{-3y^2}{(x^2+y^2+z^2)^{5/2}} + \frac{1}{(x^2+y^2+z^2)^{3/2}} \\ \frac {\partial\frac{z}{(x^2+y^2+z^2)^{3/2}}} {\partial z}= z\cdot\frac {\partial \frac{1}{(x^2+y^2+z^2)^{3/2}}}{\partial z} + \frac{1}{(x^2+y^2+z^2)^{3/2}} = \frac{-3z^2}{(x^2+y^2+z^2)^{5/2}} + \frac{1}{(x^2+y^2+z^2)^{3/2}}\end{matrix}$

L'addition de ces trois lignes donne :

$\frac{-3x^2-3y^2-3z^2}{(x^2+y^2+z^2)^{5/2}} + \frac{1+1+1}{(x^2+y^2+z^2)^{3/2}}=3-3 =0$

On a bien montré que les champs en 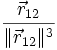$\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}$ sont tels que leur divergence est nulle :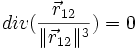 $div (\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}) = 0$

Autre notation : 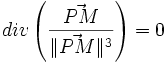$div \left(\frac{\vec {PM}}{\|\vec {PM}\|^3}\right) = 0$ et donc :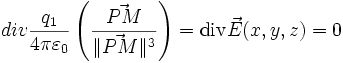 $div \frac{q_1}{4 \pi \varepsilon_0}\left(\frac{\vec {PM}}{\|\vec {PM}\|^3}\right) =\mathrm{div} \vec {E}(x,y,z) = 0$

Champ à rotationnel nul

$\overrightarrow{rot} \vec {E}(x, y, z) = \vec \nabla \ \times\vec{E}(x, y, z) = \left(\frac {\partial E_z} {\partial y}-\frac {\partial E_y} {\partial z}\right) \vec {i}+ \left(\frac {\partial E_x} {\partial z}-\frac {\partial E_z} {\partial x}\right) \vec {j} +\left(\frac {\partial E_y} {\partial x}-\frac {\partial E_x} {\partial y}\right) \vec {k}$

Or :

$\begin{matrix} \\ \frac {\partial \frac{y}{(x^2+y^2+z^2)^{3/2}}} {\partial z}= y\cdot\frac {\partial \frac{1}{(x^2+y^2+z^2)^{3/2}}}{\partial z} = \frac{-3yz}{(x^2+y^2+z^2)^{5/2}} \\ \frac {\partial \frac{z}{(x^2+y^2+z^2)^{3/2}}} {\partial y}= z\cdot\frac {\partial \frac{1}{(x^2+y^2+z^2)^{3/2}}}{\partial y} = \frac{-3zy}{(x^2+y^2+z^2)^{5/2}} \end{matrix}$

La soustraction de ces deux dernières lignes donne :

$\left(\frac {\partial E_z} {\partial y}-\frac {\partial E_y} {\partial z}\right)=\frac{-3yz+3zy}{(x^2+y^2+z^2)^{5/2}} =0$

De même avec les deux autres composantes de y et z du rotationnel.\\ On a bien montré que les chanps en 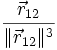$\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}$ sont tels que leur rotationnel est nul :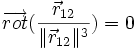 $\overrightarrow {rot} (\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}) = 0$

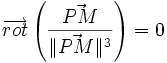
Autre notation : $\overrightarrow {rot} \left(\frac{\vec {PM}}{\|\vec {PM}\|^3}\right) = 0$

Potentiel à Laplacien nul

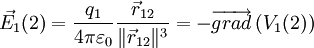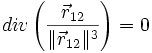
Avec : $\vec {E_1}(2) =\frac{q_1}{4 \pi \varepsilon_0} \frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}= - \overrightarrow {grad} \left( V_1(2) \right)$ et $div \left(\frac{\vec{r}_{12}}{\|\vec{r}_{12}\|^3}\right) = 0$

On obtient que : 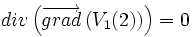$div \left( \overrightarrow {grad} \left( V_1(2) \right) \right) = 0$ sauf, bien sûr, là où il y a des charges :

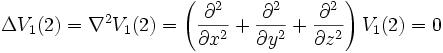$\Delta V_1(2)=\nabla^2V_1(2) =\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2} \right) V_1(2) =0$ .

qu'il faut résoudre.

Résolution de l'équation de Laplace (Δ V=0)

En cas de symétrie cylindrique ou sphérique de la distribution de charges rappelons l'expression de Δ :

En coordonnées cylindriques :

$\nabla^2 V = {1 \over r} {\partial \over \partial r} \left( r {\partial V \over \partial r} \right) + {1 \over r^2} {\partial^2 V \over \partial \phi^2} + {\partial^2 V \over \partial z^2 }$

En coordonnées sphériques :

$\nabla^2 V = {1 \over r^2} {\partial \over \partial r} \left( r^2 {\partial V \over \partial r} \right) + {1 \over r^2 \sin \theta} {\partial \over \partial \theta} \left( \sin \theta {\partial V \over \partial \theta} \right) + {1 \over r^2 \sin^2 \theta} {\partial^2 V \over \partial \phi^2}$

Donc, en cas de symétrie cylindrique V ne peut dépendre ni de θ ni de z, et dans le cas de symétrie sphérique V ne peut dépendre ni de θ ni de φ, les équations à résoudre deviennent:

En coordonnées cylindriques :

$\nabla^2 V = {1 \over r} {\partial \over \partial r} \left( r {\partial V \over \partial r} \right) + {1 \over r^2} {\partial^2 V \over \partial \phi^2} + {\partial^2 V \over \partial z^2 } = {1 \over r} {\partial \over \partial r} \left( r {\partial V \over \partial r} \right)= 0$

En coordonnées sphériques :

Toutes les deux très simples à résoudre puisque :

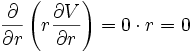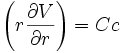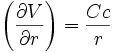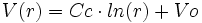
En cylindriques : ${\partial \over \partial r} \left( r {\partial V \over \partial r} \right)= 0\cdot r =0$ donne : $\left( r {\partial V \over \partial r} \right)= Cc$ soit : $\left( {\partial V \over \partial r} \right)= \frac{Cc}{r}$ et en intégrant encore : $V(r)=Cc \cdot ln(r) + Vo$

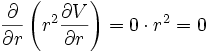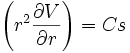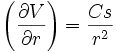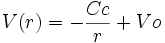
En sphériques: : ${\partial \over \partial r} \left( r^2 {\partial V \over \partial r} \right) = 0\cdot r^2 = 0$ donne:: $\left( r^2 {\partial V \over \partial r} \right) = Cs$ soit : $\left( {\partial V \over \partial r} \right)= \frac{Cs}{r^2}$ et en intégrant encore: $V(r)=-\frac{Cc}{r} + Vo$

Critique sur la notion de charge ponctuelle

La loi de Coulomb qui exprime que l'action d'une charge sur une autre est en carré de l'inverse de la distance entre les charges ne s'applique que lorsque les charges sont éloignées ; cette variation conduit à une valeur infinie si l'on prend une distance nulle. L'infini n'ayant pas de sens il est préférable d'exclure l'existence de charges ponctuelles. Si on suppose une densité de charge volumique ρ ou surfacique σ ayant la symétrie sphérique, on montre, par application du théorème mathématiques de Green que :

$\int\oint_{S} \vec E (x,y,z)\, \vec {d S}= \int\int\int_{V} div(\vec E(x,y,z)) dxdydz$

Le flux du champ électrique à travers une surface S fermée est l'intégrale sur le volume contenu dans S de la divergence du champ. Si de plus on applique le théorème de Gauss qui permet de trouver ce flux en fonction des charges intérieures :

$\int\oint_{S} \vec E(x,y,z)\, \vec {d S}= \frac{Q_i}{\epsilon_o}=\int\int\int_{V} \frac{\rho (x,y,z)}{\epsilon_o} dxdydz$

On obtient :

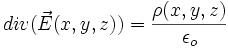 que l'on appelle « expression locale de la loi de Coulomb ».

Résolution de l'équation de Poisson (Δ V= -ρ/ε)

Là aussi limitons la résolution au cas d'une symétrie :

En cylindriques : 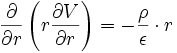${\partial \over \partial r} \left( r {\partial V \over \partial r} \right)= -\frac{\rho}{\epsilon}\cdot r$ donne : 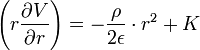$\left( r {\partial V \over \partial r} \right)= -\frac{\rho}{2\epsilon}\cdot r^2 + K$ soit : 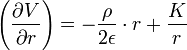$\left( {\partial V \over \partial r} \right)= -\frac{\rho}{2\epsilon}\cdot {r}+ \frac{K}{r}$ et en intégrant encore :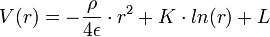 $V(r)=-\frac{\rho}{4\epsilon}\cdot r^2 + K\cdot ln(r) + L$

En sphériques: 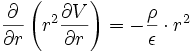${\partial \over \partial r} \left( r^2 {\partial V \over \partial r} \right) = - \frac{\rho}{\epsilon} \cdot r^2$ donne: 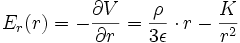$E_r(r)= - {\partial V \over \partial r} = \frac{\rho}{3\epsilon}\cdot r - \frac{K}{r^2}$ (on exclue la possibilité d'avoir un champ infini et donc on choisit $K = 0$ )

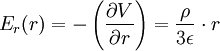
soit : $E_r(r)= - \left( {\partial V \over \partial r} \right)= \frac{\rho}{3\epsilon}\cdot r$

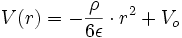
et en intégrant encore : $V(r)=-\frac{\rho}{6\epsilon}\cdot r^2 + V_o$

Principe de superposition

Le champ créé par plusieurs charges est additif (principe de superposition) :

$\vec{E_T} = \vec{E_1} + \vec{E_2} + \vec{E_3} + ...$

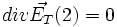
Là aussi $div \vec {E_T}(2) = 0$

Distribution de charges continue

Pour une distribution de charges continue dans l'espace, le champ vaut :

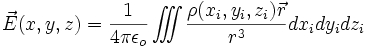$\vec{E}(x,y,z) = \frac{1}{4 \pi \epsilon_o}\int\!\!\!\!\int\!\!\!\!\int\frac{\rho(x_i,y_i,z_i)\vec{r}}{r^3} dx_idy_idz_i$ où ρ est la densité volumique de charge en i, 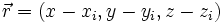$\vec{r}=(x-x_i,y-y_i,z-z_i)$ est le vecteur allant de i au point (x, y, z) ; autour du point i il y a une charge ρ $d x i d y i d z i$ .

$\vec{E}(x, y, z) = \frac{1}{4 \pi \epsilon_o}\int\!\!\!\!\int\!\!\!\!\int\frac{\rho(x_i, y_i, z_i)\vec{r}}{r^3} dx_idy_idz_i =-\vec{grad}\left({4 \pi \epsilon_o}\int\!\!\!\!\int\!\!\!\!\int\frac{\rho(x_i, y_i, z_i)}{r} dx_idy_idz_i \right)$

Magnétostatique

Champ magnétique

Le champ magnétique créé en 2 par une charge ponctuelle $q 1$ située en 1 (la charge pouvant être positive ou négative) et animée d'une vitesse v1, en unités SI :

$\vec{B_1}(2) = \frac{\mu_o}{4 \pi }\frac{q_1\vec{v}_{1}\wedge\vec{r}_{12}}{\|\vec{r}_{12}\|^3} = \frac{\mu_o q_1}{4 \pi }\;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)= 10^{-7} q_1 \;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)$

La force s'exerçant sur une charge $q 2$ plongée dans ce champ au point 2 vaut alors :

$\vec{F_1}(2) = q_2 \vec{v}_{2}\wedge\vec{B_1}(2) =q_1q_2\frac{\mu_o}{4 \pi }\left( \vec{v}_{2}\wedge\;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)\right)=10^{-7} q_1q_2 \left( \vec{v}_{2}\wedge\;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)\right)$

Si on essaie de se représenter cela en prenant pour simplifier q1 en O avec v1 suivant Oz, on a en coordonnées cylindriques :

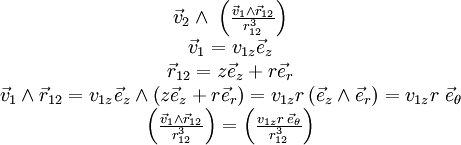
$\begin{matrix} \\ \vec{v}_{2}\wedge \;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right) \\ \vec{v}_1=v_{1z}\vec{e}_{z} \\ \vec{r}_{12}= z\vec{e}_{z}+r \vec{e}_{r} \\ \vec{v}_1\wedge\vec{r}_{12}= v_{1z}\vec{e}_{z}\wedge\left(z\vec{e}_{z}+r \vec{e}_{r}\right) =v_{1z}r \left(\vec{e}_{z}\wedge\vec{e}_{r}\right) =v_{1z}r \; \vec{e}_{\theta} \\ \left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)=\left(\frac{v_{1z}r \; \vec{e}_{\theta} }{r_{12}^3}\right) \\ \end{matrix}$

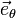
est suivant $\vec{e}_{\theta}$

et donc la force résultante est dans le plan 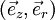$(\vec{e}_{z},\vec{e}_{r})$ comme le confirme le calcul suivant : exprimons v2 en coordonnées cylindriques : 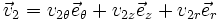$\vec{v}_2=v_{2\theta}\vec{e}_{\theta}+v_{2z}\vec{e}_{z}+v_{2r}\vec{e}_{r}$ et remplaçons le dans l'expression :

$\begin{matrix} \\ \vec{v}_{2}\wedge \;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)=\left(v_{2\theta}\vec{e}_{\theta}+v_{2z}\vec{e}_{z}+v_{2r}\vec{e}_{r}\right)\wedge \left(\frac{v_{1z}r \; \vec{e}{\theta}}{r_{12}^3}\right) \\ \;=\left(v_{2z}\vec{e}_{z}+v_{2r}\vec{e}_{r}\right)\wedge \left(\frac{v_{1z}r \; \vec{e}_{\theta}}{r_{12}^3}\right) \\ \;=\left(v_{2z}\vec{e}_{z}\right)\wedge \left(\frac{v_{1z}r \; \vec{e}_{\theta}}{r_{12}^3}\right) +\left(v_{2r}\vec{e}_{r}\right)\wedge \left(\frac{v_{1z}r \; \vec{e}_{\theta}}{r_{12}^3}\right) \\ \;=-\frac{v_{2z}v_{1z}r} {r_{12}^3}\; \vec{e}_r+\frac{v_{2r}v_{1z}r}{r_{12}^3} \; \vec{e}_z \\ \end{matrix}$

On a là le classique « deux courant parallèles et de même sens s'attirent » puisque deux charges en mouvement suivant une même direction s'attirent par effets magnétiques de l'une sur l'autre.

Champ rotationnel d'un potentiel vecteur

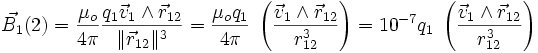
Montrons que : $\vec{B_1}(2) = \frac{\mu_o}{4 \pi }\frac{q_1\vec{v}_{1}\wedge\vec{r}_{12}}{\|\vec{r}_{12}\|^3} = \frac{\mu_o q_1}{4 \pi }\;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)= 10^{-7} q_1 \;\left(\frac{\vec{v}_{1}\wedge\vec{r}_{12}}{r_{12}^3}\right)$

est le rotationnel de : $\vec{A_1}(2) = \frac{\mu_o}{4 \pi }\frac{q_1\vec{v}_{1}}{\|\vec{r}_{12}\|} = 10^{-7} q_1 \;\left(\frac{\vec{v}_{1}}{r_{12}}\right)$

Pour simplifier plaçons q1 en O, laissons les constantes physiques de côté et remarquons que

$\begin{matrix} \\ \frac {\partial \left( \frac{1}{r} \right)} {\partial x}= \frac {\partial \left( \frac{1}{(x^2+y^2+z^2)^{1/2}} \right)} {\partial x}= - \frac {x}{(x^2+y^2+z^2)^{3/2}}=- \frac {x}{r^3 } \\ \overrightarrow{rot} \left(\frac{\vec{v}_{1}}{r}\right) = \left(\frac {\partial} {\partial y}(\frac{v_{1z}}{r}) -\frac {\partial} {\partial z}(\frac{v_{1y}}{r})\right) \vec {i}+ \left(\frac {\partial} {\partial z}(\frac{v_{1x}}{r}) -\frac {\partial} {\partial x}(\frac{v_{1z}}{r})\right) \vec {j} +\left(\frac {\partial} {\partial x}(\frac{v_{1y}}{r}) -\frac {\partial} {\partial y}(\frac{v_{1x}}{r})\right) \vec {k} \\ \overrightarrow{rot} \left(\frac{\vec{v}_{1}}{r}\right) = \left((\frac{-yv_{1z}}{r^3}) -(\frac{-zv_{1y}}{r^3})\right) \vec {i}+ \left((\frac{-zv_{1x}}{r^3}) -(\frac{-xv_{1z}}{r^3})\right) \vec {j} +\left((\frac{-xv_{1y}} {r^3}) -(\frac{-yv_{1x}}{r^3})\right) \vec {k} \\ \overrightarrow{rot} \left(\frac{\vec{v}_{1}}{r}\right) = \frac{\left(-yv_{1z}+zv_{1y} \right) \vec {i}+ \left(- zv_{1x}+xv_{1z} \right) \vec {j} +\left( -xv_{1y}+yv_{1x} \right) \vec {k}}{r^3}= \frac{\left( \vec{v}_{1}\wedge \vec{r}\right) }{r^3} \end{matrix}$

Ceci est un résultat d'analyse vectorielle, de « géométrie » ; avec le facteur des constantes physiques : 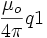$\frac{\mu_o}{4 \pi }q1$ on obtient :

$\overrightarrow{rot} \left(\frac{\vec{v}_{1}}{r}\right) = \frac{\vec{v}_{1}\wedge \vec{r} }{r^3} \ \Longleftrightarrow \ \vec{B_1}(2) = \overrightarrow{rot}\vec{A_1}(2)$

qui est une relation exprimant que le champ magnétique peut se déduire ou « dérive » d'un potentiel appelé le potentiel vecteur.

Champ à divergence nulle

$\mathrm{div} \vec {B}(x, y, z) = \vec \nabla \cdot \vec{B}(x, y, z) = \frac {\partial B_x} {\partial x} + \frac {\partial B_y} {\partial y} + \frac {\partial B_z} {\partial z}$

$\begin{matrix} = \frac{\mu_0 q_1}{4 \pi }(\frac {\partial (\frac{v_y z-v_zy}{(x^2+y^2+z^2)^{3/2}})} {\partial x} + \frac {\partial (\frac{v_zx-v_xz}{(x^2+y^2+z^2)^{3/2}})} {\partial y} + \frac {\partial (\frac{v_xy-v_yx}{(x^2+y^2+z^2)^{3/2}})} {\partial z}) \\ = \frac{\mu_0 q_1}{4 \pi } (\frac {-3x(v_y z - v_z y)-3y(v_z x - v_x z)-3z(v_x y - v_y x)}{(x^2+y^2+z^2)^{5/2}} )=0 \end{matrix}$

On a bien montré que les champs en 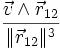$\frac{\vec v \wedge\vec{r}_{12}}{\|\vec{r}_{12}\|^3}$ sont tels que leur divergence est nulle :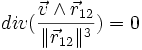 $div (\frac{\vec v \wedge\vec{r}_{12}}{\|\vec{r}_{12}\|^3}) = 0$

Autre notation : 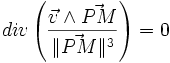$div \left(\frac{\vec v \wedge\vec {PM}}{\|\vec {PM}\|^3}\right) = 0$ et donc :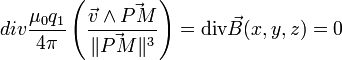 $div \frac{\mu_0 q_1}{4 \pi }\left(\frac{\vec v \wedge\vec {PM}}{\|\vec {PM}\|^3}\right) =\mathrm{div} \vec {B}(x,y,z) = 0$

Champ à rotationnel nul

$(\frac {\partial \frac{v_xy-v_yx}{(x^2+y^2+z^2)^{3/2}}}{\partial y}-\frac {\partial \frac{v_zx-v_xz}{(x^2+y^2+z^2)^{3/2}}}{\partial z})= v_x div(\frac{\vec r}{r^3}) - \vec v\cdot \vec {grad}\frac{x}{r^3}????$

Distribution continue de courant

$\vec{B}(x, y, z) = \frac{\mu_o}{4 \pi }\int\!\!\!\!\int\!\!\!\!\int\frac{\rho(x_i, y_i, z_i)\vec{v} \wedge \vec{r}}{r^3} dx_idy_idz_i = \vec{rot}\left(\frac{\mu_o}{4 \pi }\int\!\!\!\!\int\!\!\!\!\int\frac{\rho(x_i, y_i, z_i)\vec v}{r} dx_idy_idz_i \right)$

Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Électrostatique : Champ électrique • Charge électrique • Loi de Coulomb • Potentiel électrique
Magnétostatique : Champ magnétique • Moment magnétique • Loi de Biot et Savart
Électrocinétique : Champ électromagnétique • Courant de déplacement • Courant électrique • Ampère • Équations de Maxwell • Force électromotrice • Force de Lorentz • Induction électromagnétique • Loi de Lenz-Faraday • Rayonnement électromagnétique
Magnétisme : Diamagnétisme • Paramagnétisme • Superparamagnétisme • Ferromagnétisme • Antiferromagnétisme • Ferrimagnétisme • Loi de Curie • Domaine de Weiss • Susceptibilité magnétique • Perméabilité magnétique

Portail de la physique
Portail de l’électricité et de l’électronique

Ce document provient de « %C3%89lectrostatique magn%C3%A9tostatique (formulaire) ».

Catégories : Électrostatique | Magnétostatique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Electrostatique magnetostatique (formulaire) de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Electrostatique Magnétostatique (formulaire) — Électrostatique magnétostatique (formulaire) Cet article fait partie de la série formulaire de physique Optique Électro Magnéstatique Physique quantique Thermodynamique Mécanique des fluides … Wikipédia en Français
Électrostatique magnétostatique (formulaire) — Sommaire 1 Electrostatique 1.1 Force électrostatique 1.2 Champ électrostatique 1.3 Champ gradient d un potentiel … Wikipédia en Français
Formulaire d'électromagnétisme — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Electromagnetisme — Électromagnétisme L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour … Wikipédia en Français
Electromagnétisme — Électromagnétisme L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour … Wikipédia en Français
Interaction électromagnétique — Électromagnétisme L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour … Wikipédia en Français
Électromagnétique — Électromagnétisme L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour … Wikipédia en Français
Électromagnétiques — Électromagnétisme L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour … Wikipédia en Français
Électromagnétisme — L électromagnétisme est la branche de la physique qui étudie le champ électromagnétique et son interaction avec les particules dotées d une charge électrique. Le concept de champ électromagnétique a été forgé au XIXe siècle pour décrire de… … Wikipédia en Français
Electromagnétisme: lois locales et intégrales — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Electrostatique magnetostatique (formulaire)

Électrostatique magnétostatique (formulaire)

Sommaire

Electrostatique

Force électrostatique

Champ électrostatique

Champ gradient d'un potentiel

Champ à divergence nulle

Champ à rotationnel nul

Potentiel à Laplacien nul

Résolution de l'équation de Laplace (Δ V=0)

Critique sur la notion de charge ponctuelle

Résolution de l'équation de Poisson (Δ V= -ρ/ε)

Principe de superposition

Distribution de charges continue

Magnétostatique

Champ magnétique

Champ rotationnel d'un potentiel vecteur

Champ à divergence nulle

Champ à rotationnel nul

Distribution continue de courant

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Electrostatique magnetostatique (formulaire)

Électrostatique magnétostatique (formulaire)

Sommaire

Electrostatique

Force électrostatique

Champ électrostatique

Champ gradient d'un potentiel

Champ à divergence nulle

Champ à rotationnel nul

Potentiel à Laplacien nul

Résolution de l'équation de Laplace (Δ V=0)

Critique sur la notion de charge ponctuelle

Résolution de l'équation de Poisson (Δ V= -ρ/ε)

Principe de superposition

Distribution de charges continue

Magnétostatique

Champ magnétique

Champ rotationnel d'un potentiel vecteur

Champ à divergence nulle

Champ à rotationnel nul

Distribution continue de courant

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link