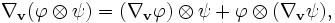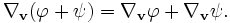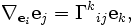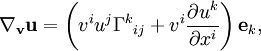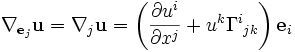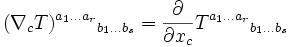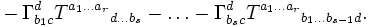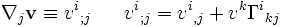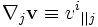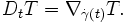- Dérivation convariante
-
Dérivée covariante
En géométrie différentielle, la dérivée covariante est un outil destiné à obtenir la dérivée d'un champ vectoriel sur une variété.
Il n'existe pas de différence entre la dérivée covariante et la connexion, à part la manière dont elles sont introduites.
Dans la théorie des variétés riemanniennes et pseudo-riemanniennes, la dérivée covariante est souvent utilisée pour la connexion de Levi-Civita.
Dans cet article, on définit la dérivée covariante (aussi connue sous le nom de dérivée de tenseur) d'un vecteur au sein d'un champ vectoriel. La dérivée covariante d'un tenseur est une extension de ce concept.
L'ensemble de cet article utilise la convention de sommation d'Einstein pour les tenseurs et les coordonnées covariantes et contravariantes. Le lecteur est supposé avoir des notions de variétés et particulièrement du vecteur tangent.
Sommaire
Concept général
La dérivée covariante
 (aussi écrite
(aussi écrite 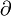 ) d'un champ de vecteur V selon la direction u est une fonction définissant un vecteur
) d'un champ de vecteur V selon la direction u est une fonction définissant un vecteur 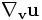 (aussi écrit
(aussi écrit 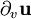 ou Dvu) qui dispose des propriétés d'une dérivée, décrites plus bas. Un vecteur est un objet géométrique indépendant du choix de la base. Lorsqu'on fixe un système de coordonnées, cette dérivée se transforme lors d'un changement de base « de la même manière » que le vecteur lui-même (selon une transformation covariante), d'où le nom de la dérivée.
ou Dvu) qui dispose des propriétés d'une dérivée, décrites plus bas. Un vecteur est un objet géométrique indépendant du choix de la base. Lorsqu'on fixe un système de coordonnées, cette dérivée se transforme lors d'un changement de base « de la même manière » que le vecteur lui-même (selon une transformation covariante), d'où le nom de la dérivée.Dans le cas d'un espace euclidien disposant d'un système de coordonnées orthonormées, on peut définir la dérivée d'un champ de vecteur en tant que différence entre deux vecteurs en deux points proches. Dans un tel système il est possible de translater un des vecteurs à l'origine de l'autre, parallèlement à lui-même. On obtient l'exemple le plus simple de dérivée covariante, obtenue en prenant la dérivée des coordonnées.
Dans le cas général, cependant, il est nécessaire de prendre en compte le changement du système de coordonnées. Par exemple, si la même dérivée covariante devait être écrite en coordonnées polaires dans un espace euclidien à deux dimensions, elle devrait contenir un terme supplémentaire décrivant la rotation des coordonnées elles-mêmes. Dans d'autres cas les termes supplémentaires décrivent comme les coordonnées s'étendent, se contractent, se déforment, ...
Un vecteur le long d'une courbe paramétrique t est exprimé dans un système de coordonnées
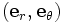 , où
, où 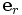 et
et 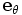 sont les vecteurs unités tangents pour les coordonnées polaires. Quelque temps après, la nouvelle base en coordonnées polaires a subi une légère rotation par rapport à la base initiale. La dérivée covariante des vecteurs de base permet d'exprimer ce changement (voir les symboles de Christoffel).
sont les vecteurs unités tangents pour les coordonnées polaires. Quelque temps après, la nouvelle base en coordonnées polaires a subi une légère rotation par rapport à la base initiale. La dérivée covariante des vecteurs de base permet d'exprimer ce changement (voir les symboles de Christoffel).Il est préférable de ne pas identifier t au paramètre temps, du moins pour les applications en relativité générale : c'est simplement un paramètre variant continûment et de manière monotone le long de la courbe. (Voir courbe paramétrique).
En espace courbe, tel que la surface de la Terre, la translation n'est pas définie, et son analogie, le transport parallèle, dépend du chemin le long duquel le vecteur est translaté.
Soit un vecteur e défini sur l'équateur d'une sphère en un point Q et dirigé vers le Nord. Supposons qu'on transporte parallèlement tout d'abord le vecteur le long de l'équateur jusqu'à P, puis (toujours grâce au transport parallèle le long d'un méridien) vers le pôle nord et enfin à nouveau jusqu'au point Q le long d'un autre méridien. On remarque que le transport parallèle de ce vecteur le long d'un circuit fermé ne retourne pas le même vecteur. A la place, il a pris une autre orientation. Ceci ne pourrait arriver dans l'espace euclidien et est causé par la courbure de la surface du globe. Le même effet peut être observé si on déplace le vecteur le long d'une surface infinitésimale. Le changement infinitésimal du vecteur est une mesure de la courbure.
Notes
Les vecteurs u et v dans la définition sont définis en un même point P. De même la dérivée covariante
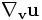 est un vecteur défini en P.
est un vecteur défini en P.La définition de la dérivée covariante n'utilise pas la métrique de l'espace. Cependant, une métrique définit de manière unique une dérivée covariante appelée la connexion de Levi-Civita.
Les propriétés de la dérivée impliquent que
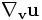 dépend du voisinage du point P de la même manière que par exemple la dérivée d'une fonction scalaire le long d'une courbe en un point P dépend du voisinage de P.
dépend du voisinage du point P de la même manière que par exemple la dérivée d'une fonction scalaire le long d'une courbe en un point P dépend du voisinage de P.La dérivée covariante peut être décrite comme un tenseur dans un système de coordonnées donné, mais ce n'est pas un tenseur dans la mesure où elle n'est pas invariante par changement de coordonnées.
L'information sur le voisinage du point P dans la dérivée covariante peut être utilisée pour définir le transport parallèle d'un vecteur. De même la courbure, la torsion et les géodésiques peuvent être définies uniquement en termes de dérivée covariante.
Définition formelle
Fonctions
Pour une fonction f, la dérivée covariante
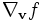 correspond à la dérivée normale d'une fonction réelle dans la direction d'un vecteur v, généralement notée
correspond à la dérivée normale d'une fonction réelle dans la direction d'un vecteur v, généralement notée 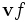 ou
ou 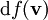 .
.Champ de vecteurs
Une dérivée covariante
 d'un champ vectoriel
d'un champ vectoriel 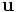 dans la direction du vecteur
dans la direction du vecteur 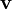 , notée
, notée 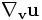 est définie par les propriétés suivantes pour tout champ de vecteur u, v, w et toutes fonctions scalaires f et g :
est définie par les propriétés suivantes pour tout champ de vecteur u, v, w et toutes fonctions scalaires f et g :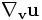 est linéaire en
est linéaire en 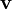 d'où
d'où 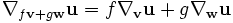
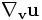 est additive en
est additive en 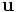 d'où
d'où 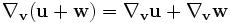
![\nabla_{\mathbf u} {\mathbf v} - \nabla_{\mathbf v} {\mathbf u} = [\mathbf u, \mathbf v]](/pictures/frwiki/101/eee6333299cb64e0262acf3020c39f72.png) où
où ![[\mathbf u, \mathbf v]](/pictures/frwiki/54/683edb00212ef113649d0bd37b69ccb4.png) est le crochet de Lie
est le crochet de Lie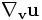 obéit aux règles générales de la dérivation concernant le produit, c'est-à-dire
obéit aux règles générales de la dérivation concernant le produit, c'est-à-dire 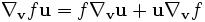 où
où 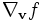 est définie plus haut.
est définie plus haut.
Noter que
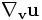 au point P dépend de la valeur de v et de P, ainsi que des valeurs de u dans un voisinage de P du fait de la dernière propriété. Ceci signifie que la dérivée covariante n'est pas un tenseur.
au point P dépend de la valeur de v et de P, ainsi que des valeurs de u dans un voisinage de P du fait de la dernière propriété. Ceci signifie que la dérivée covariante n'est pas un tenseur.Champ de tenseurs
Une fois que la dérivée covariante est définie pour les champs de vecteurs, elle peut être étendue aux champs tensoriels en utilisant les identités suivantes où
 et ψ sont deux tenseurs quelconques :
et ψ sont deux tenseurs quelconques :et si
 et ψ sont deux champs de tenseurs du même ordre alors
et ψ sont deux champs de tenseurs du même ordre alorsLa dérivée covariante d'un champ de tenseurs le long d'un vecteur v est à nouveau un champ de tenseur du même type.
Description en coordonnées
Champ de vecteurs
Soit des coordonnées
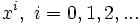 , tout vecteur tangent peut être décrit à l'aide de ses composantes dans la base ei. La dérivée covariante est un vecteur et peut ainsi être exprimée comme la combinaison linéaire Γkek de tous les vecteurs de base, où Γkek représente chacune des composantes du vecteur (en notation d'Einstein). Pour décrire la dérivée covariante il suffit de décrire celle de chacun des vecteurs de base ej le long de ei.
, tout vecteur tangent peut être décrit à l'aide de ses composantes dans la base ei. La dérivée covariante est un vecteur et peut ainsi être exprimée comme la combinaison linéaire Γkek de tous les vecteurs de base, où Γkek représente chacune des composantes du vecteur (en notation d'Einstein). Pour décrire la dérivée covariante il suffit de décrire celle de chacun des vecteurs de base ej le long de ei.Les coefficients Γki j sont appelées les symboles de Christoffel.
En utilisant ces coefficients pour des vecteurs
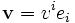 et
et 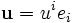 on a :
on a :Le premier terme de cette formule décrit la « déformation » du système de coordonnées par rapport à la dérivée covariante, et le second les changements de coordonnées du vecteur u. En particulier
La dérivée covariante est la dérivée selon les coordonnées à laquelle on ajoute des termes correctifs décrivant l'évolution des coordonnées.
Champ de tenseurs
La dérivée covariante d'un tenseur de type (r,s) par rapport à ec est donnée par l'expression :
Notation
Dans les ouvrages de physique, la dérivée covariante est parfois décrite à l'aide de ses composantes dans les équations.
On note souvent la dérivée covariante à l'aide d'un point-virgule, tandis que la dérivée partielle usuelle est indiquée par une virgule, sur le modèle suivant :
À nouveau, ceci montre que la dérivée covariante d'un champ vectoriel n'est pas simplement obtenue en dérivant les coordonnées vi,j, mais dépend aussi du vecteur v lui-même à travers vkΓikj.
Dans d'autres textes plus anciens (incluant l'ouvrage Introduction to General Relativity, Adler, Bazin & Schiffer), la dérivée covariante est notée à l'aide d'une double barre verticale :
Dérivée le long d'une courbe
Du fait que la dérivée covariante
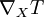 dépend uniquement de la valeur de X en un point on peut définir la dérivée covariante le long d'une courbe régulière γ(t) d'une variété :
dépend uniquement de la valeur de X en un point on peut définir la dérivée covariante le long d'une courbe régulière γ(t) d'une variété :Dans ce cas le champ tensoriel T doit être défini simplement le long de la courbe γ(t).
Parfois la dérivée covariante le long d'une courbe est qualifiée d'absolue ou dérivée intrinsèque.
Voir aussi
Bibliographie
- Claude Semay, Bernard Silvestre-Brac, Introduction au calcul tensoriel, Applications à la physique, Dunod, 2007, ISBN 978-2-10-050552-4
- Portail des mathématiques
- Portail de la physique
Catégories : Géométrie différentielle | Géométrie riemannienne | Méthode mathématique de la physique | Relativité générale
Wikimedia Foundation. 2010.