Dynamique Holomorphe

Dynamique holomorphe

La dynamique holomorphe est un domaine de l'analyse complexe et des systèmes dynamiques s'intéressant principalement à l'étude de l'itération des applications holomorphes.

Sommaire

1 Historique
2 Dynamique holomorphe à une variable
3 Espaces à paramètres
- 3.1 Théorie du potentiel en dynamique holomorphe
4 Dynamique holomorphe à plusieurs variables
5 Voir aussi

Historique

Dynamique holomorphe à une variable

L'étude de la dynamique des fonctions holomorphes à une variable est de loin la plus développée.

Afin d'établir les propriétés concernant la famille de fonctions 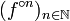$(f^{\circ n})_{n\in \mathbb{N}}$ itérées de la fonction holomorphe $f$ définie sur une variété complexe de dimension un, elle s'appuie sur les résultats de l'analyse complexe (principe du maximum, théorème des résidus, théorème de Montel, théorie des fonctions univalentes...), de la topologie générale, de la géométrie complexe (théorème d'uiformisation, hyperbolicité, théorie des applications quasi-conformes...) et de la dynamique générale.

La dualité famille normale/comportement instable qui sépare le plan dynamique en deux sous-ensembles localement discriminés en est un des faits importants. Cette dualité apparait grâce à la classification des points périodiques de la fonction $f$ , c'est-à-dire les points $z$ du domaine de définition pour lesquels il existe un entier $p$ tel que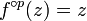 $f^{\circ p}(z)=z$ .

Introduction aux ensembles de Julia

Prenons $p (z)$ un polynôme à une variable complexe $z$ , c'est une fonction holomorphe sur $\mathbb{C}$ (l'ensemble des nombres complexes). Alors, pour chaque point de départ $z 0$ dans l'ensemble des nombres complexes, on construit la suite $(z n) n$ des itérés définie par la formule de récurrence :

z n + 1 = p (z n)

Une question naturelle est celle de la convergence de la suite $(z n) n$ , et plus généralement de son comportement (périodique, tendant vers l'infini...). On peut s'attendre, justement, à ce que le comportement de la suite dépende de la valeur initiale $z 0$ .

Par exemple, il est facile de voir que pour le polynôme $p (z) = z 2$ , si on prend une valeur initiale $z 0$ telle que $| z 0 | > 1$ , alors la suite $(z n) n$ , définie par la récurrence $z n + 1 = p (z n) = (z n) 2$ , tend vers l'infini (i.e. 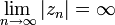$\lim_{n\rightarrow\infty}|z_n|=\infty$ . De façon plus générale, on peut montrer que pour tout polynôme $p$ , il existe un rayon $R$ tel que si $| z 0 | > R$ , alors la suite des itérés de $p$ issue de $z 0$ tend vers l'infini.

L'ensemble des points 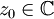$z_0\in\mathbb{C}$ tels que la suite des itérés de $p$ issue de $z 0$ tend vers l'infini est appelé bassin d'attraction de l'infini. Son complémentaire, c'est-à-dire l'ensemble des valeurs initiales $z 0$ pour lesquelles la suite $(z n) n$ ne tend pas vers l'infini, est appelé ensemble de Julia rempli.

Pour la fonction de l'exemple précédent $p (z) = z 2$ , l'ensemble de Julia rempli est le disque centré en zéro de rayon $1$ et son complémentaire le bassin de l'inifini.

L'ensemble de Julia est alors le bord de l'ensemble de Julia rempli, c'est-à-dire sa frontière topologique. Pour ce qui est de $z 2$ , son ensemble de Julia est simplement le cercle centré en zéro de rayon $1$ , cependant la "forme" des ensembles de Julia dépend évidemment de la fonction que l'on considére et est souvent bien plus complexe.

Autres exemples

Un autre exemple d'ensemble de Julia assez "simple" est celui du polynôme de Tchiébychioff $z 2 - 2$ : c'est l'intervalle $[ - 2,2]$ .

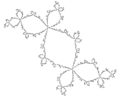
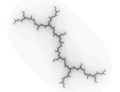
D'autres ensembles de Julia non "lisses" ont un nom (voir illustrations) :

l'ensemble de Julia du polynôme $z 2 + z$ est appelé "chou-fleur",
le lapin de Douady, représenté (entre autres) par la fonction $z 2 + + 0.123 + 0.754 i$ ,
la dendrite ( $z 2 + i$ ).

Ensemble de Julia rempli de $z 2 + z$ ,	ensemble de Julia correspondant (chou-fleur).	Un exemple de lapin de Douady (pour $z 2 + 0.123 + 0.754 i$ ).	La dendrite de $z 2 + i$ .
Poussière de Cantor (polynôme quadratique)	Ensemble de Julia de $- z 3 + z - 0.2 i$ (parties claires), le Julia rempli est composé des parties claires et vertes.

Ces ensembles sont, comme c'est le cas pour la plupart des ensembles de Julia, des fractales.

D'autres encore, sont des poussières de Cantor (par exemple $z 2 + 6 i$ ), des tapis de Sierpinsky, etc.

Caractérisation

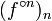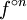Le complémentaire de l'ensemble de Julia d'une fonction holomorphe $f$ (ici un polynôme) est un ouvert $F$ , appelé ensemble de Fatou. Cet ouvert est caratérisé pas le fait que la suite de fonction $(f^{\circ n})_n$ , où $f^{\circ n}$ désigne le $n$ ième iétéré de la fonction $f$ (i.e. 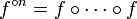$f^{\circ n} = f\circ \cdots \circ f$ $n$ fois), admet, pour tout compact $K$ inclus dans $F$ , des sous-suites uniformément convergentes sur $K$ . On dit alors que 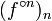$(f^{\circ n})_n$ forme une famille normale sur $F$ .

Théorie locale

L'étude locale se fait au voisinage des points périodiques de $f$ . Pour un tel point $z 0$ , il existe donc un entier naturel positif $p$ tel que 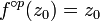$f^{\circ p}(z_0)=z_0$ . L'ensemble des images par $f$ de ce point, qui est un ensemble fini à $p$ éléments 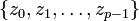$\{z_0,z_1,\dots,z_{p-1}\}$ sur lequel $f$ agit en tant qu'incrémentation d'indice modulo $p$ (i.e. 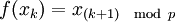$f(x_{k})=x_{(k+1)\mod\, p}$ ), est appelé un cycle périodique de $f$ .

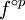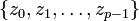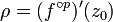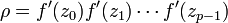La dérivée de $f^{\circ p}$ en un point du cycle périodique $\{z_0,z_1,\dots,z_{p-1}\}$ ne dépend ni point du cycle ni des cartes dans lesquelles elle est calculée. On définit le multiplicateur d'un cycle périodique comme étant la valeur $\rho=(f^{\circ p})'(z_0)$ de cette dérivée. Lorsque ce calcul peut se faire sur une seule carte on a $\rho =f'(z_0)f'(z_1)\cdots f'(z_{p-1})$ .

C'est de la valeur de $ρ$ qu'on va déduire ce qu'il se passe au voisinage des points $z i$ . L'idée principale est que l'on peut localement substituer à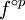 $f^{\circ p}$ le début de son développement :

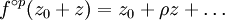$f^{\circ p}(z_0+z) = z_0 + \rho z +\dots$ ,

ou, si $ρ = 0$ :

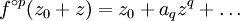$f^{\circ p}(z_0+z) = z_0 + a_q z^q +\dots$ ,

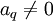avec $a_q\neq 0$ .

(...)

Théorie globale

Dynamique des polynômes

L'ensemble de Mandelbrot

Dynamique des fractions rationnelles

Dynamique des fonctions transcendantes

Espaces à paramètres

Théorie du potentiel en dynamique holomorphe

Dynamique holomorphe à plusieurs variables

Voir aussi

Portail des mathématiques

Ce document provient de « Dynamique holomorphe ».

Catégories : Systèmes dynamiques | Analyse complexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dynamique Holomorphe de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Dynamique holomorphe — La dynamique holomorphe est un domaine de l analyse complexe et des systèmes dynamiques s intéressant principalement à l étude de l itération des applications holomorphes. Sommaire 1 Historique 2 Dynamique holomorphe à une variable 2.1… … Wikipédia en Français
Système dynamique — Ne doit pas être confondu avec Dynamique des systèmes (en) Pour consulter un article plus général, voir : théorie des systèmes dynamiques. En mathématiques, en physique théorique et en ingénierie, un système dynamique est un… … Wikipédia en Français
Systeme dynamique — Système dynamique Pour consulter un article plus général, voir : Systèmes dynamiques. En mathématiques, en physique théorique et en ingénierie, un système dynamique est un système classique[1] qui évolue au cours du temps de façon à la… … Wikipédia en Français
Arithmétique complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… … Wikipédia en Français
Nombre complexe — Pour les articles homonymes, voir complexe. En mathématiques, les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels … Wikipédia en Français
Nombres complexes — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Nombres imaginaires — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Notation complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
ℂ — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Dynamique Holomorphe

Dynamique holomorphe

Sommaire

Historique