- Division entière
-
Division euclidienne
En mathématiques, et plus précisément en arithmétique, la division euclidienne ou division entière est une opération qui, à deux entiers naturels appelés dividende et diviseur, associe deux entiers appelés quotient et reste. Initialement définie pour deux entiers naturels non nuls, elle se généralise aux entiers relatifs et aux polynômes, par exemple.
Cette division est à la base des théorèmes de l'arithmétique élémentaire, comme celle de l'arithmétique modulaire qui donne lieu à la création des congruences sur les entiers.
Sommaire
Définitions
Division euclidienne dans les entiers positifs
Le théorème de division euclidienne pour des entiers positifs s'énonce ainsi : pour tous entiers a et b positifs, avec b non nul, il existe un unique couple d'entiers q et r tel que la relation a=bq+r soit vérifiée, et tel que r soit compris entre 0 et a-1 au sens large. L'entier q est appelé quotient de la division de a par b, et l'entier r reste de cette division.
DémonstrationSoient a et b deux entiers positifs, avec b non nul.
- Existence
Considérons l'ensemble E défini par :
E est non vide car il contient a. Comme E est une partie non vide de N, par axiome, le minimum de E existe. Notons r ce minimum et q l'entier qui le définit, c’est-à-dire celui vérifiant l'égalité a - b.q = r, Par construction r est un entier naturel. L'entier r - b ne peut être élément de E et donc est strictement négatif, ce qui montre que r est strictement plus petit que b. L'existence est alors démontrée.
- Unicité
Supposons qu'il existe quatre entiers q1,q2, r1 et r2 formant deux couples de solutions. Par différence, (q1 - q2).b + (r1 - r2) est nul. Cette égalité montre que b divise r1 - r2 . Comme r1 et r2 sont strictement plus petits que b et positifs, r1 - r2 est strictement compris entre - b et b. La seule valeur multiple de b possible pour r1 - r2 est donc zéro. En conclusion r1 est égal à r2 donc q1 est aussi égal à q2.
Division euclidienne dans les entiers relatifs
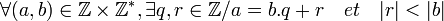
À deux entiers a et b, avec b non nul, la division euclidienne associe un quotient q et un reste r, tout deux entiers, vérifiant :
L'affirmation de l'existence du reste et du quotient est appelée Théorème de la division euclidienne pour les entiers.
S'il était possible de définir une division telle que l'unicité du quotient et du reste soit garantie, elle serait néanmoins incompatible avec le cas général de la division dans les anneaux euclidiens.
DémonstrationLa définition de la division euclidienne sur les entiers naturels permet de prouver l'existence de deux entiers naturels q1 et r1 tels que
- | a | = | b | q1 + r1 avec r1 < | b |
Une petite étude sur les signes respectifs de a et b permet de donner pour la division euclidienne de a par b
- pour a et b négatifs , quotient q1 et reste - r1
- pour a négatif et b positf , quotient - q1 et reste - r1
- pour a positif et b négatif , quotient - q1 et reste r1
- Pour a et b positifs, quotient q1 et reste r1
Mais l'unicité n'est pas toujours acquise si l'on n'impose pas r positif ou nul. En effet si a = bq + r avec r strictement positif alors a = b(q+1) + r - b dans lequel | r − b | < | b | fournit un autre couple solution.
Division euclidienne dans l'ensemble des polynômes
Article détaillé : Division d'un polynôme.La division euclidienne selon les puissances décroissantes existe si l'anneau est défini sur un corps :
![\forall (A,B)\in\mathbb{K}[X]\times\mathbb{K}[X]^*,\quad \exists !Q, R\in\mathbb{K}[X], A=B.Q+R \quad avec \quad \operatorname{deg}(R) < \operatorname{deg}(B)](/pictures/frwiki/50/2630f301bb91125be04dbf453fc1749b.png)
À deux polynômes A et B à coefficients dans un corps K avec B non nul, la division euclidienne associe un unique quotient Q et un unique reste R, tout deux polynômes, vérifiant :
L'unicité est ici garantie, en revanche il est nécessaire que K soit un corps. Sinon la division est encore parfois possible, si par exemple le coefficient du monôme dominant de B est égal à 1, ou plus généralement si le coefficient du monôme dominant de B est inversible.
Division euclidienne dans un anneau
Article détaillé : Anneau euclidien.Dans certains types d'anneaux commutatifs unitaires intègres, on peut définir une division euclidienne par
- a = bq + r avec r = 0 où v(r) < v(b) v étant une application de A - { 0 } dans
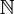 appelée stathme euclidien.
appelée stathme euclidien.
S'il existe un stathme euclidien sur l'anneau A, il en existe un qui vérifie la propriété suivante : si a et b sont deux éléments de A tel que b divise a, alors v(b)
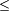 v(a). Un anneau admettant un stathme euclidien est appelé anneau euclidien. La définition d'un stathme euclidien diffère d'un auteur à l'autre. Les rapports logiques entre les différentes définitions sont abordés dans l'article Anneau euclidien.
v(a). Un anneau admettant un stathme euclidien est appelé anneau euclidien. La définition d'un stathme euclidien diffère d'un auteur à l'autre. Les rapports logiques entre les différentes définitions sont abordés dans l'article Anneau euclidien.Algorithmes de calcul
On s'intéresse au calcul de division euclidienne de deux entiers, connaissant au préalable les opérations d'addition, de soustraction, de multiplication, et de comparaison, entre des nombres entiers. Il est facile de ramener le problème à deux entiers positifs, et on se restreint à ce cas.
Les algorithmes décrits ci-dessous calculent le quotient de la division euclidienne ; il est bien clair que le reste s'en déduit. Attention, le contraire ne serait pas vrai.
La première méthode, naturelle mais naïve, demande beaucoup trop de calculs pour des grands nombres. On présente ensuite deux méthodes courantes, de complexité semblable : la première convient pour des calculs en base 2, et donc pour une programmation informatique ; la deuxième méthode, essentiellement équivalente, est une adaptation pour la base de numération habituelle, la base décimale, et convient donc pour des calculs à la main. C'est l'algorithme enseigné à l'école.
Méthode naïve
Pour effectuer la division euclidienne de a par b, on construit une suite strictement décroissante (ai) définie par une relation de récurrence de pas 1 : a0 = a, puis
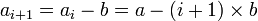 . Il existe donc un plus petit entier I tel que aI < b : c'est-à-dire
. Il existe donc un plus petit entier I tel que aI < b : c'est-à-dire 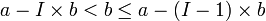 , ce qui s'écrit encore
, ce qui s'écrit encore 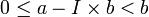 . Le quotient de la division cherchée est donc I, et le reste
. Le quotient de la division cherchée est donc I, et le reste 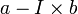 .
.Le nombre de pas de cet algorithme est donc
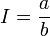 ; chaque étape requiert une soustraction et une comparaison ; la complexité de calcul croît linéairement avec a, c'est-à-dire exponentiellement avec la taille de a - si on convient de mesurer la taille d'un entier par le nombre de chiffres que requiert son développement binaire (ou décimal si on préfère, cela ne modifie les choses que d'une constante), cette taille est de l'ordre du logarithme de l'entier.
; chaque étape requiert une soustraction et une comparaison ; la complexité de calcul croît linéairement avec a, c'est-à-dire exponentiellement avec la taille de a - si on convient de mesurer la taille d'un entier par le nombre de chiffres que requiert son développement binaire (ou décimal si on préfère, cela ne modifie les choses que d'une constante), cette taille est de l'ordre du logarithme de l'entier.Méthode courante, binaire
Une simple amélioration consiste à faire une recherche dichotomique, sur le quotient : au lieu de parcourir comme précédemment tous les entiers depuis 0 en attendant de tomber sur le bon quotient, on va commencer par trouver rapidement un entier dont on sera sûr qu'il est plus grand que le quotient cherché ; dans la liste finie de quotients possibles restants, on fera une recherche dichotomique.
Le premier calcul se fait simplement en considérant la suite géométrique 2n. Tant que
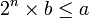 , on incrémente n de 1 à chaque étape. Soit N le plus petit entier tel que
, on incrémente n de 1 à chaque étape. Soit N le plus petit entier tel que 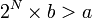 . Le nombre d'étapes pour trouver cet entier est de l'ordre de
. Le nombre d'étapes pour trouver cet entier est de l'ordre de 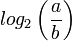 . Chacune de ces étapes ne demande qu'une multiplication par deux (encore plus facile qu'une addition, pour une écriture binaire), et une comparaison.
. Chacune de ces étapes ne demande qu'une multiplication par deux (encore plus facile qu'une addition, pour une écriture binaire), et une comparaison.Pour le deuxième calcul, on construit deux suites (αn) et (βn) ; l'une stockera des minorants du quotient cherché, l'autre des majorants stricts. On pose donc α0 = 2N − 1 et β0 = 2N, puis par récurrence :
- si
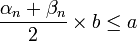 , alors on peut affiner le minorant, et on pose donc
, alors on peut affiner le minorant, et on pose donc 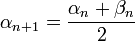 et
et 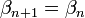
- en revanche, si
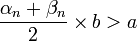 , on peut affiner le majorant, et on pose
, on peut affiner le majorant, et on pose 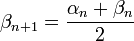 , et
, et 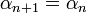 .
.
On montre facilement par récurrence qu'à chaque étape n de ce deuxième calcul, αn et βn sont deux entiers, tous deux multiples de 2N − 1 − n et dont la différence vaut 2N − 1 − n ; cette remarque permet notamment de montrer que les suites sont bien définies jusqu'à n = N − 1, et que αN − 1 et βN − 1 ne diffèrent que de 1 ; puisqu'ils sont respectivement un minorant large et un majorant strict du quotient, αN − 1est le quotient cherché.
Le nombre maximal d'étapes pour ce calcul est de l'ordre de
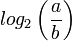 (une des dichotomies a pu donner le bon quotient avant la N - 1ème étape, c'est le cas d'égalité de la comparaison, auquel cas on peut arrêter l'algorithme avant), qui chacune n'exige qu'une addition, une division par deux (facile en écriture binaire, ce n'est évidemment pas une division euclidienne cachée), une multiplication (qui peut être évitée, en gérant plus de variables), et une comparaison.
(une des dichotomies a pu donner le bon quotient avant la N - 1ème étape, c'est le cas d'égalité de la comparaison, auquel cas on peut arrêter l'algorithme avant), qui chacune n'exige qu'une addition, une division par deux (facile en écriture binaire, ce n'est évidemment pas une division euclidienne cachée), une multiplication (qui peut être évitée, en gérant plus de variables), et une comparaison.En concaténant les résultats des deux calculs, on voit que cet algorithme a une complexité qui croît logarithmiquement avec
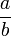 , et donc linéairement avec la taille de a . L'amélioration est donc très nette.
, et donc linéairement avec la taille de a . L'amélioration est donc très nette.Méthode courante, décimale
Soit deux entiers naturels a et
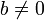 dont on veut effectuer la division. On commence par trouver la plus petite puissance de 10 telle que
dont on veut effectuer la division. On commence par trouver la plus petite puissance de 10 telle que 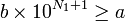 ; d'après le théorème de division euclidienne, il existe alors un unique entier
; d'après le théorème de division euclidienne, il existe alors un unique entier 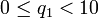 tel que :
tel que : 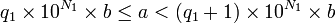 . On se ramène donc à faire la division de
. On se ramène donc à faire la division de 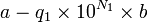 par b ; l'inégalité précédente montre que la première puissance de 10 telle que
par b ; l'inégalité précédente montre que la première puissance de 10 telle que 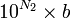 excèdera
excèdera 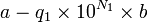 sera strictement plus petite que
sera strictement plus petite que 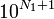 ; on la note
; on la note 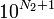 . On construit ainsi une suite d'entiers naturels (Ni) strictement décroissante ; elle vaut donc 0 à un certain rang ; on construit la suite d'entiers
. On construit ainsi une suite d'entiers naturels (Ni) strictement décroissante ; elle vaut donc 0 à un certain rang ; on construit la suite d'entiers 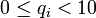 associée de la même façonqu'on a construit q1. Le quotient cherché sera
associée de la même façonqu'on a construit q1. Le quotient cherché sera 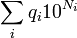 : en effet l'inégalité qui donne qr pour la première occurrence de Nr = 0 sera :
: en effet l'inégalité qui donne qr pour la première occurrence de Nr = 0 sera : 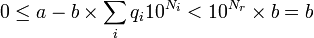 , ce qui est bien la définition du quotient.
, ce qui est bien la définition du quotient.On remarque que cette méthode se divise comme la précédente en deux étapes : d'abord une recherche d'une puissance assez grande, ce qui demande à nouveau un nombre de calcul logarithmique en a, c'est-à-dire linéaire en la taille de a ; ensuite un calcul de tous les coefficients qi associés au différentes puissances de 10 inférieures à la puissance assez grande obtenue. Pour chaque calcul de qi, l'algorithme demande en fait un calcul de division euclidienne intermédiaire ; mais le quotient est à chercher seulement parmi les entiers de 0 à 9 ; il se fait donc rapidement en utilisant des tables.
Cette méthode est celle utilisée en primaire lorqu'il s'agit de poser une division.
Dans d'autres anneaux
Voir aussi
À lire avant
À lire après
- Portail des mathématiques
Catégories : Divisibilité et factorisation | Opération | Anneau | Arithmétique modulaire
Wikimedia Foundation. 2010.

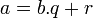
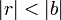
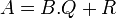
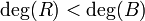

 Reste euclidien
Reste euclidien

 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit