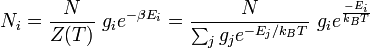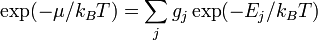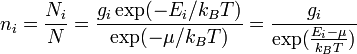Distribution de Maxwell

Statistique de Maxwell-Boltzmann

Cet article fait partie de la série
Mécanique quantique

$\hat H | \psi\rangle = i\hbar\frac{{\rm d}}{{\rm d}t}|\psi\rangle$

Concepts fondamentaux
État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence

Expériences
Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect

Formalisme
Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction

Statistiques
Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson

Théories avancées
Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman

Interprétations
Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente)

Physiciens
Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

La statistique de Maxwell-Boltzmann est une loi de probabilité ou distribution utilisée en physique statistique pour déterminer la répartition des particules entre différents niveaux d'énergie. Elle est notamment à la base de la théorie cinétique des gaz.

Sommaire

1 Énoncé
- 1.1 Formulation discrète
- 1.2 Formulation continue
2 Limitations
3 Applications
- 3.1 Biophysique
4 Voir aussi
- 4.1 Articles connexes

Énoncé

Formulation discrète

On se donne un système de $N$ particules n'interagissant pas entre elles et pouvant prendre les différents états d'énergie discrets $E i$ . Le nombre $N i$ de particules dans un état d'énergie donné $E i$ est :

$N_i = \frac{N}{Z(T)}~ g_i e^{-\beta E_i} = \frac{N}{\sum_{j} g_j e^{-E_j/k_{B}T}}~ g_i e^{\frac{-E_i}{k_{B}T}}\,$

où

$g i$ est la dégénérescence de l'état d'énergie E_i, c'est-à-dire le nombre d'états possédant l'énergie $E i$ ;
$k B$ est la constante de Boltzmann ;
$T$ est la température du système (celui-ci doit donc être à l'équilibre) ;
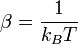
$\beta = \frac{1}{k_B T}$
$Z (T)$ est la fonction de partition du système.

Formulation continue

On considère un système de $N$ particules sans interaction entre elles et pouvant prendre continûment tout état d'énergie entre zéro et l'infini. Le nombre d $N E$ de particules possédant une énergie entre $E$ et $E + d E$ est :

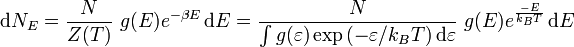$\mathrm{d}N_E = \frac{N}{Z(T)}~ g(E)e^{-\beta E}\, \mathrm{d}E = \frac{N}{\int g(\varepsilon)\exp\left(-\varepsilon/k_{B}T\right) \mathrm{d}\varepsilon}~ g(E)e^{\frac{-E}{k_{B}T}} \, \mathrm{d}E$ ,

où

$g (E)$ est la dégénérescence du système (densité de probabilité des états ayant une énergie comprise entre $E$ et $E + d E$ ) ;
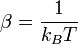
$\beta = \frac{1}{k_B T}$
$Z (T)$ est la fonction de partition du système.

Limitations

La statistique de Maxwell-Boltzmann a été bâtie en supposant l'absence d'interaction entre les particules concernées : elle n'est donc valable en toute rigueur que pour un gaz parfait classique. Elle est toutefois utilisable aussi comme approximation du comportement d'un gaz réel quand il est possible de négliger les interactions entre ses particules, mais ne peut s'appliquer, par exemple, à aucun liquide.

De plus, cette statistique est construite dans le cadre de la mécanique classique; elle ne s'applique donc que lorsque les effets quantiques sont négligeables, par exemple à des températures suffisamment hautes. À basse température, elle doit être remplacée par la statistique de Bose-Einstein pour les bosons et la statistique de Fermi-Dirac pour les fermions.

Pour comparer ces trois statistiques, il est utile de reformuler la statistique de Maxwell-Boltzmann en posant :

$\exp ( - \mu / k_{B}T ) = { \sum_{j} g_j \exp ( - E_j / k_{B}T ) } \,$

d'où :

$n_i = \frac{N_i} {N} = \frac{ g_i \exp ( - E_i / k_{B}T ) } { \exp ( - \mu / k_{B}T ) } = \frac{g_i} { \exp ( \frac{ E_i - \mu } {k_{B}T} ) } \,$

Applications

Biophysique

En neurosciences, on décrit souvent les mécanismes d'ouverture et de fermeture des Canaux ioniques par une fonction de Boltzmann simplifiée quand ceux-ci sont dépendants du potentiel de membrane. La formule utilisée est alors:

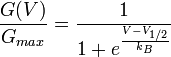$\frac{G(V)}{G_{max}}=\frac{1}{1+e^{\frac{V-V_{1/2}}{k_{B}}}}$ ,

où

V est le potentiel de membrane,
G(V) est la conductance ionique associée aux canaux, dépendante du potentiel de membrane,
G_max est la conductance maximale,
V_1/2 est le potentiel de membrane pour lequel la moitié des canaux sont ouverts,
k est la dépendance de l'ouverture des canaux par rapport au changement de potentiel, décrit dans la littérature comme étant la « constante de pente ».

La fonction de Boltzmann est ici utilisée pour décrire les résultats expérimentaux issus de la mesure patch-clamp des courants de membrane, et ainsi determiner les propriétés des différentes catégories de courants membranaires. Les paramètres V_1/2 et k sont determinants pour la modélisation informatique des propriétés électriques d'une cellule nerveuse.

Voir aussi

Sur les autres projets Wikimedia :

Statistique de Maxwell-Boltzmann, sur Wikiversity (communauté pédagogique libre)

Regardez d'autres dictionnaires:

distribution de Maxwell — Maksvelo skirstinys statusas T sritis fizika atitikmenys: angl. Maxwell distribution; Maxwellian distribution vok. Maxwellsche Verteilung, f; Maxwell Verteilung, f rus. распределение Максвелла, n pranc. distribution de Maxwell, f; distribution… … Fizikos terminų žodynas
Distribution de Maxwell-Boltzmann — Statistique de Maxwell Boltzmann Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique … Wikipédia en Français
Maxwell–Boltzmann distribution — Maxwell–Boltzmann Probability density function Cumulative distribution function parameters … Wikipedia
Distribution De Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… … Wikipédia en Français
Distribution de boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… … Wikipédia en Français
Distribution de Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… … Wikipédia en Français
Maxwell distribution — Maksvelo skirstinys statusas T sritis fizika atitikmenys: angl. Maxwell distribution; Maxwellian distribution vok. Maxwellsche Verteilung, f; Maxwell Verteilung, f rus. распределение Максвелла, n pranc. distribution de Maxwell, f; distribution… … Fizikos terminų žodynas
Maxwell-Verteilung — Maksvelo skirstinys statusas T sritis fizika atitikmenys: angl. Maxwell distribution; Maxwellian distribution vok. Maxwellsche Verteilung, f; Maxwell Verteilung, f rus. распределение Максвелла, n pranc. distribution de Maxwell, f; distribution… … Fizikos terminų žodynas
distribution maxwellienne — Maksvelo skirstinys statusas T sritis fizika atitikmenys: angl. Maxwell distribution; Maxwellian distribution vok. Maxwellsche Verteilung, f; Maxwell Verteilung, f rus. распределение Максвелла, n pranc. distribution de Maxwell, f; distribution… … Fizikos terminų žodynas
Distribution Gamma — Loi Gamma Densité de probabilité / Fonction de masse Fonction de répartition > … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Distribution de Maxwell

Statistique de Maxwell-Boltzmann

Sommaire