Dallages

Un pavage (ou dallage) est une partition d’un espace (généralement un espace euclidien comme le plan ou l’espace tridimensionnel) par un ensemble fini d’éléments appelés tuiles (plus précisément, ce sont des compacts d’intérieur non vide). Généralement, on considère des pavages par translations, c’est-à-dire que deux mêmes tuiles du pavage sont toujours déductibles l’une de l’autre par une translation (à l’exclusion des rotations ou symétries). Il existe aussi des pavages d’espaces non euclidien, les plus célèbres étant sans doute les nombreux pavages de M.C. Escher (pavages d’espaces hyperboliques).

Sommaire 1 Pavages périodiques 2 Pavages apériodiques 3 Pavages quasipériodiques 4 Notes et références 5 Voir aussi 5.1 Bibliographie 5.2 Articles connexes 5.3 Liens externes

Pavages périodiques

Les pavages périodiques du plan ou de l’espace sont connus depuis l’antiquité et ont souvent été utilisés comme motifs décoratifs en architecture.

En cristallographie, ces pavages modélisent les arrangements périodiques d’atomes (cristaux). En 1891, le cristallographe et mathématicien russe Fedorov (Université de Saint-Petersbourg) a montré qu’il existait seulement 17 types de groupes cristallographiques du plan (groupes d’isométries contenant un sous-groupe discret bidimensionnel de translations).

Par la suite, Heinrich Heesch a montré en 1968^[1] qu’il existait 28 types de pavés (ou tuiles). Toutefois, cette classification peut être améliorée car certains des 28 types sont cas particuliers d’autres.

En fait, à chacun des groupes cristallographiques, à deux exceptions près, correspond un seul type de pavé. A chacune de ces exceptions, (pg et pgg), sont associés 2 types de pavés. Au total, il existe donc 19 types de pavés pour les pavages périodiques du plan.

Plusieurs de ces types, peuvent être réalisés par des pavages dont les pavés sont toutes des polygones réguliers. L’Alhambra de Grenade contient des mosaïques illustrant presque tous les types de pavages.

Pavages apériodiques

Les mathématiciens ont longtemps pensé que les seuls pavages par translations du plan étaient nécessairement périodiques.

Notamment, Hao Wang a conjecturé en 1961 que c’était le cas, et en a déduit qu’on pouvait concevoir un programme informatique qui déciderait si un jeu de tuiles donné permettait de paver ou non le plan. Cependant, en 1964, Robert Berger (un élève de Wang) a trouvé un ensemble de 20 426 tuiles ne pouvant paver qu’apériodiquement le plan. La conjecture est donc fausse : savoir si un jeu de tuiles peut paver ou non le plan est indécidable.

Des jeux toujours plus petits de tuiles ne pavant qu’apériodiquement ont depuis été trouvés :

• en 1976, Raphael Robinson simplifie le jeu de tuiles de Robert Berger en un jeu de 24 tuiles (6 à rotation près) ;
• en 1974, Roger Penrose, trouve un jeu de 20 tuiles (2 à rotation près) donnant le pavage de Penrose ;
• en 1996, Karel Culik et Jarkko Kari ont trouvé (par une méthode complètement différente) un jeu de 13 tuiles.

En 1994, John Horton Conway et Charles Radin ont trouvé un jeu comportant une infinité de tuiles mais qui, à rotation près, se réduit à une unique tuile : un triangle rectangle de côtés 1, 2 et 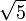. Le pavage obtenu est connu sous le nom de Pinwheel.

Pavages quasipériodiques

Parmi les pavages apériodiques, certains le sont moins que d’autres… en d’autres termes, on peut quantifier le degré d’apériodicité.

Dans cette voie, on peut citer par exemple les notions de récurrence et de récurrence uniforme (ou quasipériodicité).

Un pavage est dit récurrent si, quand un motif (ensemble fini de tuiles) apparaît une fois, il apparaît dans n’importe quelle zone suffisamment grande. Si, de plus, on peut fixer la taille de cette zone en fonction de la taille du motif, alors le pavage est dit uniformément récurrent (ou quasipériodique).

Ainsi, un pavage uniformément récurrent du plan est tel que si on considère n’importe quel un motif apparaissant dans un cercle de rayon r tracé sur le pavage, alors il existe un nombre R tel qu’on puisse être sûr que ce motif réapparaisse dans n’importe quel cercle de rayon R tracé sur le pavage.

En particulier, les pavages périodiques sont uniformément récurrents (a fortiori récurrents). C’est aussi le cas du pavage de Penrose. En fait, on peut montrer que si un jeu de tuile pave le plan, alors il peut aussi le paver de manière uniformément récurrente (la preuve repose sur un argument diagonal).

Notes et références

Voir aussi

Bibliographie

• Tangente n^o 99 : « L’art des pavages » (juillet-août 2004).

Articles connexes

• Pavé
• Frise
• Cristallographie
• Polyomino

Liens externes

• Kali, pour tracer des pavages
• Animation des 17 pavages du plan
• (en) Sur le pavage
• Artiste français présentant son livre sur les pavages
• (en) The Tilings Encyclopedia
• Description des 19 types de pavés du plan

• Portail de la géométrie