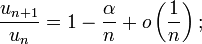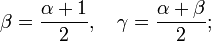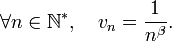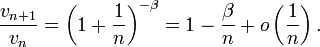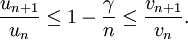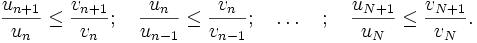Critère de Raabe-Duhamel
- Critère de Raabe-Duhamel
-
Règle de Raabe-Duhamel
En mathématiques, la règle de Raabe-Duhamel est une technique permettant d'établir la convergence d'une série. Elle tire son nom des mathématiciens Joseph Raabe et Jean-Marie Duhamel.
Démonstration
Notons
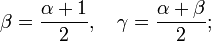
et
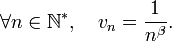
On a
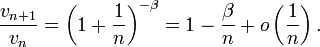
Supposons α > 1. Comme 1 < β < γ < α, au delà d'un certain rang N on a
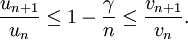
On a donc tout une liste de majoration
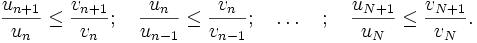
Et donc par multiplication, on obtient 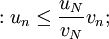 par comparaison, la convergence de
par comparaison, la convergence de 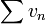 entraîne bien celle de
entraîne bien celle de 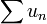 .
.
Or β > 1, donc l'exemple de la série de Riemann montre que 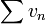 converge, et donc
converge, et donc 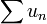 converge.
converge.
Le cas α < 1 se traite de manière analogue.
Ce théorème est un complément à la règle de d'Alembert pour séries à termes réels positifs et permet donc de le préciser.
 Portail des mathématiques
Portail des mathématiques
Catégories : Énoncé mathématique | Suite
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Critère de Raabe-Duhamel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Critère — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un critère (du grec kriterion, de krinein, juger) est un principe auquel on se réfère, ou un moyen qu on utilise, pour établir un jugement. Cette notion… … Wikipédia en Français
Jean-Marie Duhamel — Pour les articles homonymes, voir Duhamel. Jean Marie Constant Duhamel Jean Marie Constant Duhamel, né à Saint Malo le 5 février … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Règle de Cauchy — Pour les articles homonymes, voir Cauchy. En mathématiques et en topologie, la règle de Cauchy, qui doit son nom au mathématicien français Augustin Cauchy, est un critère de convergence pour une série à termes réels, ou complexes, ou plus… … Wikipédia en Français
Serie convergente — Série convergente En mathématiques, une série est dite convergente si la suite de ses sommes partielles a une limite dans l espace considéré. Dans le cas contraire, elle est dite divergente. Pour des séries numériques, ou à valeurs dans un espace … Wikipédia en Français
Série convergente — En mathématiques, une série est dite convergente si la suite de ses sommes partielles a une limite dans l espace considéré. Dans le cas contraire, elle est dite divergente. Pour des séries numériques, ou à valeurs dans un espace de Banach, il… … Wikipédia en Français
SÉRIES ET PRODUITS INFINIS — La notion de limite d’une suite est à la base de l’analyse. Le langage des séries, équivalent à celui des suites, s’est imposé dès le XVIIe siècle à propos du développement des fonctions en série entière. Cependant, les fondements rigoureux de la … Encyclopédie Universelle
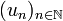 une suite de nombres réels à termes strictement positifs telle que
une suite de nombres réels à termes strictement positifs telle que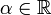 , alors
, alors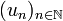 diverge,
diverge,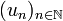 converge,
converge,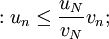 par comparaison, la convergence de
par comparaison, la convergence de 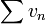 entraîne bien celle de
entraîne bien celle de 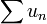 .
.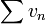 converge, et donc
converge, et donc 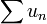 converge.
converge.