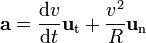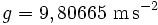Vecteur accélération

Accélération

L'accélération désigne couramment une augmentation de la vitesse; en physique, plus précisément en cinématique, l'accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d'un mouvement en fonction du temps.

Dans le langage courant, l'accélération s'oppose à la décélération et indique l'augmentation de la vitesse de l'évolution d'un processus quelconque, par exemple l'accélération du rythme cardiaque ou l'accélération des évènements d'une actualité.

Sommaire

1 Applications
- 1.1 Calcul de la distance parcourue
  - 1.1.1 Exemple
2 Accélération en mécanique
3 Accélération de la convergence en mathématiques
4 Voir aussi
- 4.1 Articles connexes

Applications

Dans la vie courante, on distingue trois événements que le physicien regroupe sous le seul concept d'accélération :

aller plus vite (accélérer au sens commun plus restrictif) : l'accélération est positive, c'est-à-dire que le vecteur accélération possède une composante dans le sens de la vitesse
aller moins vite (freiner ou décélérer ou ralentir dans le langage commun) : l'accélération est négative, ou le vecteur accélération possède une composante opposée au sens de la vitesse
changer de direction (tourner ou virer dans le langage commun) : l'accélération comporte une composante perpendiculaire à la vitesse, si celle-ci change de direction sans changer de norme

La notion d'accélération est formalisée par Pierre Varignon (1654-1722) le 20 janvier 1700, comme un écart infiniment petit de vitesse $d v$ sur le temps infiniment petit $d t$ mis pour modifier cette vitesse. Réitérant l'approche qu'il avait utilisé deux ans plus tôt pour définir la notion de vitesse, il utilise le formalisme du calcul différentiel mis au point quelques années plus tôt par Leibniz (1646-1716).

Calcul de la distance parcourue

Par exemple, vous souhaitez calculer la distance parcourue par un solide en mouvement accéléré, dans le cas où l'accélération $a$ est constante. Dans la formule ci-dessous, $d 0$ représente le déplacement initial, $v 0$ la vitesse initiale, $Δ t$ la durée du trajet et $a$ l'accélération :

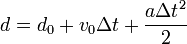
$d = d_{0}+v_{0} {\Delta t} + \frac{a{\Delta t}^2}{2}$

Exemple

Afin de déterminer la hauteur d'un pont, on lâche une pierre depuis le haut du-dit pont. Celle-ci met la durée $Δ t = 2,5$ secondes pour atteindre le sol. Quelle est la distance parcourue ?

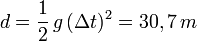
Sachant que a=g=9,81 m.s^-2, la distance parcourue est $d = \frac{1}{2}\,g\, (\Delta t)^2 = 30,7\, m$

Accélération en mécanique

En dynamique, l'accélération 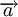$\overrightarrow{a}$ subie par un corps est liée à la force 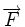$\overrightarrow{F}$ totale exercée sur celui-ci par l'intermédiaire de la seconde loi de Newton (ou principe fondamental de la dynamique) selon laquelle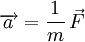

$\overrightarrow{a} = \frac{1}{m} \, \vec{F}$

où m est la masse du corps.
Cette équation signifie que toute force appliquée à un objet produit automatiquement une accélération, quelle que soit la masse de cet objet.

L'accélération d'un point peut donc se calculer par la seconde loi de Newton, mais il existe une autre méthode pour la calculer, lorsque l'équation horaire du mouvement est donnée ou calculable facilement : il s'agit de dériver cette équation horaire du mouvement une première fois (ce qui nous donnera la valeur de la vitesse en fonction du temps), puis une deuxième fois, ce qui donnera la valeur de l'accélération en fonction du temps.

Accélération moyenne

L'accélération moyenne a sur un intervalle de temps Δt est définie de la manière suivante :

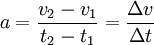
$a = \frac{v_2 - v_1}{t_2 - t_1} = \frac{\Delta v}{\Delta t}$

v₁ est la vitesse (vectorielle) à l'instant t₁ et v₂ est la vitesse à l'instant t₂.

v₁ - v₂ est un vecteur. Il est parfois commode de distinguer l'accélération tangentielle (dans le sens du mouvement, selon le vecteur 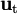$\mathbf{u}_\mathrm{t}$ : variation de vitesse absolue) et l'accélération normale (perpendiculaire au mouvement, selon le vecteur 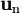$\mathbf{u}_\mathrm{n}$ : à vitesse absolue constante) :

$\mathbf{a} = \frac{\mathrm{d}v}{\mathrm{d}t} \mathbf{u}_\mathrm{t} + \frac{v^2}{R}\mathbf{u}_\mathrm{n}$

Accélération et gravité

Article détaillé : g (accélération).

La gravité provoque l'accélération d'une masse qui n'est soumise qu'à cette seule force, lors du mouvement qui par définition est appelé la chute libre. L'intensité de la gravité subie par un corps est donc exprimée sous la forme d'une accélération, notée 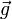$\vec{g}$ . Afin de donner une valeur « parlante », on exprime souvent une accélération par rapport à l'accélération moyenne de la gravité sur Terre, en g :

$g = 9,80665\ \mathrm{m\, s^{-2}}$

À partir du constat que masse grave et masse inerte ne peuvent être distinguées fonctionnellement, la relativité générale admet, sous le nom de principe d'équivalence, que la gravité ne se distingue pas localement (c'est-à-dire si l'on considère uniquement un point) d'une accélération. Il est important sur le plan conceptuel de connaître cette équivalence, beaucoup de physiciens utilisant pour cette raison, en abrégé, le terme accélération pour désigner indifféremment une modification de vitesse ou la présence dans un champ de gravité, même en l'absence apparente (dans l'espace 3D) de mouvement.

Variations d'accélération

Tout comme le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps on peut définir la dérivée de l'accélération par rapport au temps. Il s'agit du vecteur jerk qui permet ainsi de quantifier les variations d'accélération et qui est utilisé dans un certain nombre de domaines.

Accélération de la convergence en mathématiques

Le terme est aussi utilisé en mathématiques, par exemple l'accélération de la convergence d'une suite (par des procédés comme le Delta-2 d'Aitken) signifie que l'écart entre la valeur des éléments de la suite et sa limite est plus petit que pour la suite initiale à un rang n donné.

Voir aussi

Voir « accélération » sur le Wiktionnaire.

Regardez d'autres dictionnaires:

accélération — [ akselerasjɔ̃ ] n. f. • 1327; lat. acceleratio, de accelerare 1 ♦ Cour. Augmentation de vitesse. L accélération d un mouvement. Cette voiture a des accélérations foudroyantes. Fig. Le fait d aller plus vite. L accélération du pouls, de la… … Encyclopédie Universelle
Acceleration — Accélération L accélération désigne couramment une augmentation de la vitesse; en physique, plus précisément en cinématique, l accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d un mouvement en fonction… … Wikipédia en Français
Accélération gravitationnelle — Accélération L accélération désigne couramment une augmentation de la vitesse; en physique, plus précisément en cinématique, l accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d un mouvement en fonction… … Wikipédia en Français
Accélération moyenne — Accélération L accélération désigne couramment une augmentation de la vitesse; en physique, plus précisément en cinématique, l accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d un mouvement en fonction… … Wikipédia en Français
Accélération verticale — Accélération L accélération désigne couramment une augmentation de la vitesse; en physique, plus précisément en cinématique, l accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d un mouvement en fonction… … Wikipédia en Français
Accélération tangentielle — ● Accélération tangentielle projection orthogonale du vecteur accélération sur le vecteur vitesse … Encyclopédie Universelle
Accélération — Pour les articles homonymes, voir Accélération des ordinateurs parallèles. On appelle couramment accélération l augmentation de la vitesse ; en physique, plus précisément en cinématique, l accélération est une grandeur vectorielle qui… … Wikipédia en Français
Acceleration centripete — Accélération centripète Vecteurs de position et d accélération dans un mouvement circulaire En cinématique du point, l accélération centripète est l accélération, dirigée vers le centre, d un point en rotation autour d un axe fixe. Si le point… … Wikipédia en Français
Accélération Centripète — Vecteurs de position et d accélération dans un mouvement circulaire En cinématique du point, l accélération centripète est l accélération, dirigée vers le centre, d un point en rotation autour d un axe fixe. Si le point tourne autour du centre à… … Wikipédia en Français
Acceleration de Coriolis — Accélération de Coriolis L accélération de Coriolis (nommée ainsi en l honneur du savant français Gaspard Gustave Coriolis) est un terme d accélération qui intervient lorsque l on étudie le mouvement d un corps se déplaçant dans un référentiel en … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Vecteur accélération

Accélération

Sommaire