Corps totalement reel

Corps totalement reel

Corps totalement réel

En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l'ensemble des nombres complexes, l'image se trouve dans l'ensemble des nombres réels. De manière équivalente, K est engendré sur 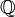\mathbb{Q}\, par une racine d'un polynôme à coefficients entiers P dont toutes les racines sont réelles, ou bien encore le produit tensoriel 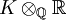K\otimes_\mathbb{Q}\mathbb{R} est un produit d'exemplaires de \mathbb{R}. La notion de signature d'un corps de nombres permet de mesurer plus précisément à quel point un corps est loin d'être totalement réel.

Par exemple, les corps quadratiques sont soit totalement réels, soit complexes, suivant qu'ils sont engendrés par la racine carrée d'un nombre positif ou négatif. Dans le cas des corps cubiques, un polynôme P irréductible de degré 3 à coefficients entiers aura au moins une racine réelle. S'il possède une racine réelle et deux complexes, l'extension cubique correspondante de 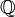\mathbb{Q}\, définie en adjoignant la racine réelle ne sera pas totalement réelle, bien qu'elle soit incluse dans le corps des nombres réels.

Les corps totalement réels jouent un rôle spécial significatif dans la théorie algébrique des nombres ; ils sont l'objet par exemple de la conjecture de Greenberg. Une extension abélienne de 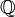\mathbb{Q}\, est soit totalement réelle, soit un corps à multiplication complexe, c'est-à-dire une extension quadratique totalement imaginaire d'un corps totalement réel.

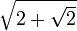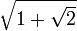Un nombre algébrique est dit totalement réel si tous ses conjugués (autrement dit les racines complexes de son polynôme minimal) sont réels. La plus petite extension normale contenant ce nombre est alors un corps totalement réel. Ainsi \sqrt{2} et \sqrt{2+\sqrt{2}} sont totalement réels, mais ni \sqrt[3]{2} ni \sqrt{1+\sqrt{2}} ne le sont.

Références

  • Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
  • (en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Corps totalement r%C3%A9el ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Corps totalement reel de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Corps Totalement Réel — En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière équivalente, K est… …   Wikipédia en Français

  • Corps totalement réel — En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière équivalente, K est… …   Wikipédia en Français

  • Corps de nombres totalement réel — Corps totalement réel En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière… …   Wikipédia en Français

  • Corps totalement ordonné — Corps ordonné En algèbre générale, un corps ordonné est la donnée d un corps , muni d une relation d ordre (notée dans l article) compatible avec la structure de corps. Dans tout l article, on note naturellement la relation d ordre réciproque de …   Wikipédia en Français

  • Corps cyclotomique — Extension cyclotomique En théorie algébrique des nombres, on appelle extension cyclotomique du corps des nombres rationnels, les surcorps de la forme où ζn est une racine primitive nème de l unité ; cette appellation provient de ce que ces… …   Wikipédia en Français

  • Corps Ordonné — En algèbre générale, un corps ordonné est la donnée d un corps , muni d une relation d ordre (notée dans l article) compatible avec la structure de corps. Dans tout l article, on note naturellement la relation d ordre réciproque de , et l on note …   Wikipédia en Français

  • Corps ordonne — Corps ordonné En algèbre générale, un corps ordonné est la donnée d un corps , muni d une relation d ordre (notée dans l article) compatible avec la structure de corps. Dans tout l article, on note naturellement la relation d ordre réciproque de …   Wikipédia en Français

  • Corps des réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… …   Wikipédia en Français

  • Corps ordonné — En algèbre générale, un corps ordonné est la donnée d un corps commutatif (K, +, ×), muni d une relation d ordre (notée ≤ dans l article) compatible avec la structure de corps. Dans tout l article, on note naturellement ≥ la relation d ordre… …   Wikipédia en Français

  • Corps réel clos — En mathématiques, un corps réel clos est un corps totalement ordonné F tel que tout élément positif soit un carré et que tout polynôme de degré impair à coefficients dans F ait au moins une racine dans F. Le corps des réels, le corps des réels… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”