- Abélianisé
-
Groupe dérivé
Dans un groupe G, le groupe dérivé, noté D(G) ou [G,G], est le plus petit sous-groupe normal pour lequel le quotient G/[G,G] est abélien. Le groupe dérivé de G est trivial ssi le groupe G est abélien. Le quotient de G par son groupe dérivé est l'abélianisé de G.
Le procédé d'abélianisation permet en pratique de prouver que deux groupes ne sont pas isomorphes. Il intervient aussi en géométrie.
Sommaire
Commutateurs
Le commutateur de deux éléments
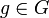et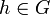 
est par définition l'élément [g,h] défini par:![[g,h]= g h g^{-1} h^{-1}\,](/pictures/frwiki/53/5e048ef166234472d4f08eac9e197017.png)
.Certains ouvrages définissent le commutateur de g et de h comme g − 1h − 1gh ; ce n'est pas la convention ici adoptée.
Le commutateur mesure le défaut de commutation des éléments g et h :
gh = [g,h]hg et donc : ![[g,h]=e\Leftrightarrow gh=hg](/pictures/frwiki/48/04019051fd50cd0c9c62dfede0c6ce59.png)
En particulier, dans un groupe abélien G, tous les commutateurs valent l'élément neutre e.
- L'inverse du commutateur de g et de h est le commutateur de h et de g :
[g,h] − 1 = [h,g] - Les commutateurs sont stables par les automorphismes de G. Pour tout automorphisme ψ et pour tous g et h dans G :
ψ([g,h]) = [ψ(g),ψ(h)] - Pour tous g, h, et k dans G, on a :
[g,hk] = [g,h].h[g,k]h − 1 Groupe dérivé
L'ensemble des commutateurs est stable par l'inverse mais pas nécessairement par composition. Il n'est pas, en général, un sous-groupe de G. Le sous-groupe engendré par les commutateurs est appelé le groupe dérivé de G, noté D(G) ou [G,G].
![D(G) = [G,G] = < \{ [g,h] \, | \, (g,h) \in G^2 \} >](/pictures/frwiki/100/dd482d3696d99a73c24777612202bfeb.png)
En particulier tout élément de D(G) est un produit fini de commutateurs. Comme l'image d'un commutateur par un automorphisme de groupe est un commutateur, le groupe dérivé est stable par les automorphismes de G : c'est un sous-groupe caractéristique. Par suite, c'est un sous-groupe normal.
Exemples : Le groupe dérivé du groupe symétrique
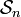est le groupe alterné 
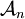.Abélianisé
Comme [G,G] est un sous-groupe normal de G, on peut définir le quotient de G par [G,G], par définition l'abélianisé de G :
Ab(G) = Gab = G / [G,G] - Pour tout groupe G, son abélianisé Ab(G) est un groupe abélien.
En effet, pour tout élément g et h de G, on a : gh = hg[g − 1,h − 1]. Donc, modulo le groupe dérivé, g et h commutent.
- L'abélianisé est le plus grand quotient abélien de G au sens où tout sous-groupe normal dont le quotient correspondant est abélien contient le groupe dérivé de G.
Si H est un sous-groupe normal de G, et que G/H est abélien, alors, pour tous éléments g et h, il existe x dans H tel que : gh = hgx. De fait, x est le commutateur de g − 1 et h − 1.
La propriété précédente se reformule en termes de morphismes. Tout morphisme surjectif d'un groupe vers un groupe abélien se factorise à travers l'abélianisé.
Suite dérivée
La suite dérivée de G est la suite des sous-groupes de G définie par récurrence :
![D^k(G)=D\left[D^{k-1}(G)\right]=[D^{k-1}(G),D^{k-1}(G)]](/pictures/frwiki/54/6c22fab7d9643a4e3be14d74ebf68b61.png)
Si cette suite est stationnaire à {e}, c'est à dire il existe un naturel non nul n tel que Dn(G) = {e}, le groupe est dit résoluble.
Portail des mathématiques
Catégorie : Théorie des groupes
Wikimedia Foundation. 2010.
