Conjecture De Leopoldt

Conjecture De Leopoldt

Conjecture de Leopoldt

En théorie algébrique des nombres, la conjecture de Leopoldt, du nom du mathématicien Heinrich Wolfgang Leopoldt, qui l'a formulée en 1962 dans un article paru au Journal de Crelle, est un énoncé central, à la fois par le nombre de ses formulations équivalentes, touchant aux divers objets de la théorie, et par la richesse de ses conséquences. Il n'est actuellement démontré que pour le cas des extensions abéliennes du corps des nombres rationnels, par des méthodes relevant de l'étude de l'indépendance des nombres algébriques, à la suite de travaux d'Ax et Brumer, et pour certaines extensions de corps quadratiques imaginaires.

Quelques formulations

Soit k un corps de nombres algébriques, et p un nombre premier. La conjecture de Leopoldt en p pour le corps k indique que ce corps n'admet que r2+1 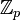\mathbb{Z}_p-extensions linéairement indépendantes, où r2 désigne le nombre de couples de plongements complexes conjugués du corps k, et où 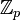\mathbb{Z}_p est l'anneau des entiers p-adiques, vu ici comme limite projective des groupes abéliens 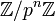\mathbb{Z}/p^n\mathbb{Z}. Ceci peut encore se formuler en disant que le groupe de Galois de la pro-p-extension abélienne maximale du corps k, a pour rang r2+1 en tant que 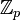\mathbb{Z}_p-module.

A travers la théorie du corps de classes, cet énoncé peut se reformuler en l'énoncé suivant sur le groupe des unités E du corps k : l'application obtenue à partir de l'application diagonale, partant du tensorisé 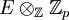E\otimes_\mathbb{Z}\mathbb{Z}_p, et à valeurs dans le produit des groupes d'unités locaux en les places de k au-dessus de p 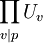\prod_{v\mid p} U_v est injective (et donc a pour rang r1+r2-1, d'après le théorème des unités de Dirichlet, ce qui est à comparer avec le 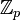\mathbb{Z}_p-rang de l'espace d'arrivée, qui est r1+2r2).

Références

  • (en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]
  • (en) Lawrence C. Washington, Introduction to cyclotomic fields [détail des éditions]


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Conjecture de Leopoldt ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture De Leopoldt de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Conjecture de leopoldt — En théorie algébrique des nombres, la conjecture de Leopoldt, du nom du mathématicien Heinrich Wolfgang Leopoldt, qui l a formulée en 1962 dans un article paru au Journal de Crelle, est un énoncé central, à la fois par le nombre de ses… …   Wikipédia en Français

  • Conjecture de Leopoldt — En théorie algébrique des nombres, la conjecture de Leopoldt, du nom du mathématicien Heinrich Wolfgang Leopoldt (en), qui l a formulée en 1962 dans un article paru au Journal de Crelle, est un énoncé central, à la fois par le nombre de ses… …   Wikipédia en Français

  • Leopoldt's conjecture — In algebraic number theory, Leopoldt s conjecture, introduced by H. W. Leopoldt (1962, 1975), states that p adic regulator of a number field does not vanish. The p adic regulator is an analogue of the usual regulator defined using p adic… …   Wikipedia

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Preda Mihăilescu — Preda V. Mihăilescu (né le 23 mai 1955 à Bucarest) est un mathématicien roumain connu pour sa démonstration de la conjecture de Catalan. Il est le frère de l anthropologiste Vintilă Mihăilescu. Après avoir quitté la Roumanie en 1973, il …   Wikipédia en Français

  • Théorie d'Iwasawa — La théorie d Iwasawa peut être vue comme une tentative d étendre les résultats arithmétiques classiques sur les corps de nombres (extensions finies du corps des rationnels) à des extensions infinies de , par des procédés de passage à la limite… …   Wikipédia en Français

  • Theorie d'Iwasawa — Théorie d Iwasawa La théorie d Iwasawa peut être vue comme une tentative d étendre les résultats arithmétiques classiques sur les corps de nombres (extensions finies du corps des rationnels) à des extensions infinies de , par des procédés de… …   Wikipédia en Français

  • Théorème de Baker — Le théorème de Baker résout la conjecture de Gelfond. Dû à Alan Baker dans une série d articles intitulés Linear forms in the logarithms of algebraic numbers parue en 1966 et 1967 dans la revue Mathematika, c est un résultat de transcendance sur… …   Wikipédia en Français

  • Théorème de baker — Le théorème de Baker, dû à A. Baker dans une série d articles intitulés Linear forms in the logarithms of algebraic numbers parue en 1966 et 1967 dans la revue Mathematika, est un résultat de transcendance sur les logarithmes de nombres… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”