Plongement complexe
- Plongement complexe
-
Signature (arithmétique)
En théorie algébrique des nombres, la signature d'un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et r2 le nombre de couples de plongements complexes conjugués du corps K ; un plongement, injection dans le corps algébriquement clos des nombres complexes, est considéré réel s'il est à valeurs dans le sous-corps des nombres réels, et complexe sinon.
C'est un fait classique en théorie des corps que chaque plongement complexe admet un plongement complexe conjugué, ainsi que la relation r1+2r2=n, où n est le degré du corps K sur le corps des nombres rationnels.
La signature d'un corps de nombres intervient dans de nombreuses formules arithmétiques, comme le théorème des unités de Dirichlet, ou le dénombrement des 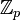 -extensions linéairement indépendantes, en théorie d'Iwasawa.
-extensions linéairement indépendantes, en théorie d'Iwasawa.
Références
- (en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie algébrique des nombres
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Plongement complexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Plongement réel — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et … Wikipédia en Français
Theoreme des unites de Dirichlet — Théorème des unités de Dirichlet En théorie algébrique des nombres, le théorème des unités de Dirichlet détermine la structure du groupe des unités d un corps de nombres des entiers algébriques d un corps de nombres K. Le groupe des unités… … Wikipédia en Français
Théorème des unités de Dirichlet — Pour les articles homonymes, voir Théorème de Dirichlet. En théorie algébrique des nombres, le théorème des unités de Dirichlet détermine la structure du groupe des unités de l anneau des entiers algébriques d un corps de nombres K. Le groupe des … Wikipédia en Français
Théorème des unités de dirichlet — En théorie algébrique des nombres, le théorème des unités de Dirichlet détermine la structure du groupe des unités d un corps de nombres des entiers algébriques d un corps de nombres K. Le groupe des unités désigne l ensemble des éléments… … Wikipédia en Français
Signature (arithmetique) — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et … Wikipédia en Français
Signature (arithmétique) — Pour les articles homonymes, voir Signature (homonymie). En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Groupe Des Classes D'idéaux — En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des classes d idéaux 2 Développement… … Wikipédia en Français
Groupe des classes — d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des classes d idéaux 2… … Wikipédia en Français
Groupe des classes d'ideaux — Groupe des classes d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des… … Wikipédia en Français
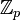 -extensions linéairement indépendantes, en théorie d'Iwasawa.
-extensions linéairement indépendantes, en théorie d'Iwasawa.