Abréviation en mathématiques

Abréviation en mathématiques: Liste des abréviations en mathématiques

Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Cette page présente quelques sigles et abréviations utilisés couramment en mathématiques.

Lettres grecques

π (pi) : nombre pi

Π (pi majuscule) : produit formel

Σ (sigma majuscule) : somme

ζ (dzêta ou zêta) : désigne une des fonctions dzêta

A

ach ou acosh ou argch : cosinus hyperbolique réciproque

acos ou arccos : arc cosinus

ash ou asinh ou argsh : sinus hyperbolique réciproque

asin ou arcsin : arc sinus

atan ou arctan : arc tangente

arctg (ancien) : arc tangente

ath ou atanh ou argth : tangente hyperbolique réciproque

C

$\mathbb{C}$ : ensemble des nombres complexes

ch : cosinus hyperbolique

cns : condition nécessaire et suffisante (équivalence)

cos : cosinus

cosec : cosécante

cosech : cosécante hyperbolique

cotan : cotangente

cotg (ancien) : cotangente

D

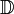$\mathbb D$ : ensemble des nombres décimaux

E

E : en typographie simplifiée, note les puissances de dix : 3E-2 = 3·10^-2

e : base de l'exponentielle

Ei : exponentielle intégrale

exp : exponentielle

H

$\mathbb{H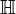}$ : ensemble des quaternions

L

li : logarithme intégral

ln ou Log : logarithme népérien

log : logarithme ; logarithme décimal

N

$\mathbb{N}$ : ensemble des entiers naturels

Q

$\mathbb{Q}$ : ensemble des nombres rationnels

R

$\mathbb{R}$ : ensemble des nombres réels

√ : radical (Racine carrée, cubique...)

S

sec : sécante

sech : sécante hyperbolique

sh : sinus hyperbolique

Si : sinus intégral

sin : sinus

sinc : sinus cardinal

T

tan : tangente

tanh ou th : tangente hyperbolique

tg : tangente (ancien)

Z

$\mathbb{Z}$ : ensemble des entiers relatifs

Jargon

Les abréviations suivantes ne sont pas utilisables au sein d'une formule; elles sont des abréviations linguistiques.

BON : base orthonormée

BOND : base orthonormée directe

CQFD : ce qu'il fallait démontrer

iid : indépendamment et identiquement distribués (en statistiques)

inv : fonction involute

QED : quod erat demonstrandum (cf. CQFD)

RON : repère orthonormé, voir base orthonormale

ROND : repère orthonormé direct

ssi : si et seulement si, voir équivalence logique

Articles connexes

Table des symboles mathématiques

Catégorie:Symbole mathématique

Portail des mathématiques

Ce document provient de « Liste des abr%C3%A9viations en math%C3%A9matiques ».

Catégories : Vocabulaire des mathématiques | Abréviation | Liste en rapport avec les mathématiques

Sommaire :	Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Contenu soumis à la licence CC-BY-SA. Source : Article Abréviation en mathématiques de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Axiome (Mathématiques Élémentaires) — Axiome Un axiome (du grec ancien αξιωμα/axioma, « considéré comme digne, convenable, évident en soi ») désigne une vérité indémontrable qui doit être admise. Pour certains philosophes grecs de l Antiquité, un axiome était une… … Wikipédia en Français
Axiome (mathematiques elementaires) — Axiome Un axiome (du grec ancien αξιωμα/axioma, « considéré comme digne, convenable, évident en soi ») désigne une vérité indémontrable qui doit être admise. Pour certains philosophes grecs de l Antiquité, un axiome était une… … Wikipédia en Français
Axiome (mathématiques élémentaires) — Axiome Un axiome (du grec ancien αξιωμα/axioma, « considéré comme digne, convenable, évident en soi ») désigne une vérité indémontrable qui doit être admise. Pour certains philosophes grecs de l Antiquité, un axiome était une… … Wikipédia en Français
CQFD (Abréviation) — Pour les articles homonymes, voir CQFD (homonymie) et QED (homonymie). CQFD (ou c.q.f.d.[1]) est l abréviation de « ce qu il fallait démontrer ». Elle se place à la fin d une démonstration mathématique pour indiquer que le résultat… … Wikipédia en Français
CQFD (abreviation) — CQFD (abréviation) Pour les articles homonymes, voir CQFD (homonymie) et QED (homonymie). CQFD (ou c.q.f.d.[1]) est l abréviation de « ce qu il fallait démontrer ». Elle se place à la fin d une démonstration mathématique pour indiquer… … Wikipédia en Français
Cqfd (abréviation) — Pour les articles homonymes, voir CQFD (homonymie) et QED (homonymie). CQFD (ou c.q.f.d.[1]) est l abréviation de « ce qu il fallait démontrer ». Elle se place à la fin d une démonstration mathématique pour indiquer que le résultat… … Wikipédia en Français
Répertoire bibliographique des sciences mathématiques — Le répertoire bibliographique des sciences mathématiques (RBSM) est l une des premières tentatives de classement systématique des articles, monographies et mémoires présentant un intérêt pour les sciences mathématiques. Décidé en 1885 par la… … Wikipédia en Français
Classe (Mathématiques) — Pour les articles homonymes, voir Classe. En mathématiques, la notion de classe généralise celle d ensemble. Les deux termes sont parfois employés comme synonymes, mais la théorie des ensembles distingue ces deux notions. Un ensemble peut être vu … Wikipédia en Français
CQFD (abréviation) — Pour les articles homonymes, voir CQFD (homonymie) et QED (homonymie). CQFD (ou C. Q. F. D.[1]) est l abréviation de « ce qu il fallait démontrer ». Elle se place à la fin d une démonstration mathématique pour indiquer que le résultat… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Abréviation en mathématiques

Liste des abréviations en mathématiques

Lettres grecques

A

C

D

E

H

L

N

Q

R

S

T

Z

Jargon

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Abréviation en mathématiques

Liste des abréviations en mathématiques

Lettres grecques

A

C

D

E

H

L

N

Q

R

S

T

Z

Jargon

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link