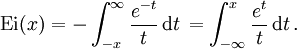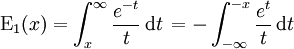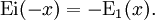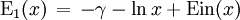Exponentielle Intégrale
- Exponentielle Intégrale
-
Exponentielle intégrale
En mathématiques, l'exponentielle intégrale Ei(x) est définie par :
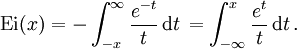
Comme 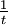 diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy.
diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy.
L'exponentielle intégrale a pour développement en série :
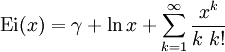 ,
,
où γ est la constante d'Euler-Mascheroni.
Elle est reliée à une autre fonction définie par :
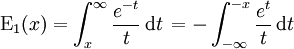
Cette fonction étend l'exponentielle intégrale au réels négatifs compte tenu de l'identité :
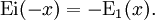
Les deux fonctions s'expriment en fonction de la fonction entière définie par :
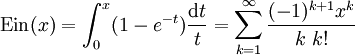 .
.
En effet, on peut écrire :
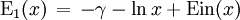
et
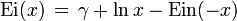 .
.
 Portail des mathématiques
Portail des mathématiques
Catégories : Fonction remarquable | Fonction hypergéométrique | Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Exponentielle Intégrale de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Exponentielle integrale — Exponentielle intégrale En mathématiques, l exponentielle intégrale Ei(x) est définie par : Comme diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy. L exponentielle intégrale a pour développement… … Wikipédia en Français
Exponentielle intégrale — En mathématiques, l exponentielle intégrale Ei(x) est définie par : Comme diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy. L exponentielle intégrale a pour développement en série … Wikipédia en Français
Integrale de chemin — Intégrale de chemin Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes)… … Wikipédia en Français
Intégrale De Chemin — Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme pour les… … Wikipédia en Français
Integrale de Gauss — Intégrale de Gauss Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi … Wikipédia en Français
Intégrale De Gauss — Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur … Wikipédia en Français
Intégrale de gauss — Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur … Wikipédia en Français
EXPONENTIELLE ET LOGARITHME — Pour les constructeurs des premières tables, les logarithmes étaient avant tout un outil de calcul numérique; mais leur importance n’a cessé de croître. Il suffira de feuilleter cette encyclopédie pour constater que, de nos jours, les logarithmes … Encyclopédie Universelle
Intégrale de chemin — Une intégrale de chemin (« path integral » en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme… … Wikipédia en Français
Intégrale de Gauss — La surface comprise entre la courbe d équation y = exp(−x2) et l axe des abscisses vaut √π. En mathématiques, une intégrale de Gauss est l intégrale d une fonction gaussienne sur l ensemble des réels. Sa valeur est reliée à la constante π par la… … Wikipédia en Français
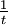 diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy.
diverge pour t=0, cette intégrale doit être comprise en termes de valeur principale de Cauchy.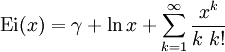 ,
,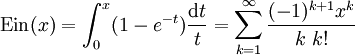 .
.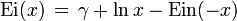 .
.