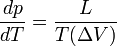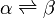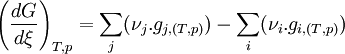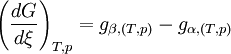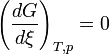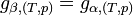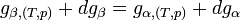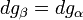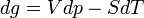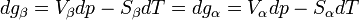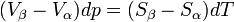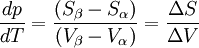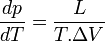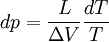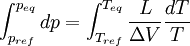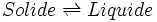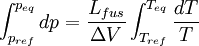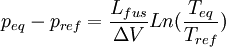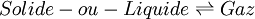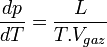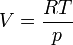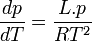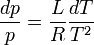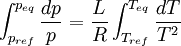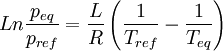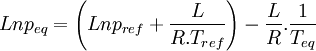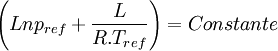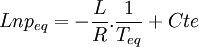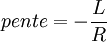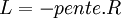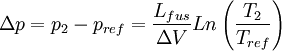Clausius-Clapeyron

Formule de Clapeyron

Pour les articles homonymes, voir Clapeyron.

La formule de Clapeyron ou relation de Clausius-Clapeyron est une relation permettant de définir l'évolution de la pression d'équilibre en fonction de la température d'équilibre au cours d'un changement d'état physique d'un corps pur. La connaissance expérimentale de cette évolution de la pression en fonction de la température d'équilibre, permet la détermination de la chaleur latente L du changement d'état ou plus généralement du changement de phase.

Sommaire

1 Expression différentielle de la formule de Clapeyron
2 Établissement de la formule de Clapeyron
3 Relations de Clapeyron intégrées
4 Diagramme de Clapeyron
5 Applications
6 Notes et références de l'article
7 Voir aussi
- 7.1 Articles connexes
- 7.2 Liens externes

Expression différentielle de la formule de Clapeyron

$\frac{dp}{dT} = \frac{L}{T(\Delta V)}~$

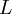$L~$ : Chaleur latente équivalente à ΔH ( variation d'enthalpie ) de changement d'état, effectué à pression constante.

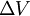$\Delta V~$ : variation de volume au cours du changement de phase.

Cette formule n'est valable que dans le cas d'une transition de phase du premier ordre (pour les transitions de phase du deuxième ordre voir les formules d'Ehrenfest).

Établissement de la formule de Clapeyron

Un changement d'état physique est une transformation de la matière. Il est caractérisé par la coexistence de deux phases pures et s'effectue généralement, à température et pression constantes. La seule variable indépendante du système est alors la variable de composition ξ, permettant de définir les quantités de chaque phase à l'équilibre. On peut alors considérer le changement d'état comme une sorte de réaction chimique particulière effectuée à T et p constante mais sans qu'il y ait changement de la nature chimique des constituants; la seule variable étant également la variable ξ. Les formules établies lors de l'étude de l'équilibre chimique peuvent être parfaitement adaptées au cas du changement d'état.

Considérons le changement d'état défini par l'équation suivante, mettant en jeu les phases α et β à T et p constantes:

$\alpha \rightleftharpoons \beta~$

Appliquons la relation concernant l'enthalpie libre, obtenue dans le cas d'un équilibre chimique:

$\left(\frac {dG}{d\xi}\right)_{T,p} = \sum_j(\nu_j.g_{j,(T,p)}) - \sum_i(\nu_i.g_{i,(T,p)})~$

Dans le cas d'un changement d'état cela devient:

$\left(\frac {dG}{d\xi}\right)_{T,p} = g_{\beta,(T,p)} - g_{\alpha,(T,p)}~$

Or, à l'équilibre

$\left(\frac {dG}{d\xi}\right)_{T,p} = 0~$

Donc, à l'équilibre les potentiels chimiques des deux phases sont égaux

$g_{\beta,(T,p)} = g_{\alpha,(T,p)}~$

Si l'on modifie la pression d'équilibre, la température d'équilibre sera modifiée (par exemple l'eau bout à 100 °C sous la pression de 1 atm mais si la pression diminue, la température d'ébullition diminue aussi). Les enthalpies libres des deux phases α et β varient elles aussi, mais elles sont toujours égales lorsque le système atteint son nouvel équilibre. On peut écrire:

$g_{\beta,(T,p)} + dg_{\beta} = g_{\alpha,(T,p)} + dg_{\alpha}~$

$dg_{\beta} = dg_{\alpha}~$

L'enthalpie libre d'un corps pur dépend de T et de p. La différentielle est égale à:

$dg = Vdp - SdT~$

d'où

$dg_{\beta} = V_{\beta}dp - S_{\beta}dT = dg_{\alpha} = V_{\alpha}dp - S_{\alpha}dT~$

Il s'ensuit

$(V_{\beta} - V_{\alpha})dp = (S_{\beta} -S_{\alpha})dT ~$

d'où

$\frac {dp}{dT} = \frac {(S_{\beta} -S_{\alpha})}{(V_{\beta} - V_{\alpha})} = \frac{\Delta S}{\Delta V}~$

Le changement d'état a lieu à pression constante donc la chaleur latente mise en jeu, L, est égale à la variation d'enthalpie ΔH = Q_p. Si la transformation présente un caractère de réversibilité, ΔS = Q_p / T = L / T.

$\frac {dp}{dT} = \frac {L}{T.\Delta V}~$

Relations de Clapeyron intégrées

$\frac {dp}{dT} = \frac {L}{T.\Delta V}~$

d'où

$dp = \frac {L}{\Delta V} \frac{dT}{T}~$

Considérons deux états d'équilibre dont un état de référence connu, caractérisés par les couples de paramètres: état 1 de référence (p_ref, T_ref); état 2 (p_eq, T_eq). Intégrons la relation de Clapeyron entre ces deux états d'équilibre.

$\int_{p_{ref}}^{p_{eq}}dp = \int_{T_{ref}}^{T_{eq}} \frac {L}{\Delta V} \frac{dT}{T}~$

La chaleur latente dépend, en toute rigueur de la température, mais on peut par approximation la considérer comme constante même si l'intervalle de T est de l'ordre quelques dizaines voire quelques centaines de degrés. En revanche la variation de volume ne peut plus être considérée comme constante si l'une des phase est gazeuse. Cela dépend donc du type de changement d'état.

Équilibre de fusion-solidification

$Solide \rightleftharpoons Liquide~$

Dans ce cas il n'y a que des phases condensées dont le volume molaire est très faible par rapport à celui des gaz^[1]. Donc la variation de volume est très faible et elle reste pratiquement constante entre les deux états d'équilibre. On obtient alors:

$\int_{p_{ref}}^{p_{eq}}dp = \frac {L_{fus}}{\Delta V}\int_{T_{ref}}^{T_{eq}} \frac{dT}{T}~$

d'où

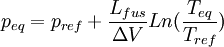
$p_{eq} - p_{ref} = \frac {L_{fus}}{\Delta V} Ln (\frac{T_{eq}}{T_{ref}})~$

$p_{eq} = p_{ref} + \frac {L_{fus}}{\Delta V} Ln (\frac{T_{eq}}{T_{ref}})~$

La courbe associée à cette relation correspond à la branche d'équilibre de fusion-solidification, sur le diagramme de Clapeyron: Péq = f(Téq). Cette branche est presque linéaire aux basses pressions et est pratiquement verticale à cause de la faible valeur de la variation de volume constatée pour les phases condensées. Pour la quasi-totalité des composés, la pente est positive. L'eau est une exception (ainsi que le bismuth, l'antimoine, le germanium...) car le volume du solide (glace) est supérieur à celui du liquide ( la glace flotte ) et donc ΔV est négative ainsi que la pente de la branche.

Équilibre de sublimation-condensation ou vaporisation-condensation

$Solide -ou-Liquide \rightleftharpoons Gaz~$

Ces deux équilibres sont caractérisés par la coexistence d'une phase condensée et d'un gaz. Elle correspondent donc au même cas de figure. Comme le volume molaire d'un gaz est très supérieur à celui d'un liquide ou d'un solide, on pourra négliger ce dernier devant le volume du gaz: ΔV ≅ V(gaz). Mais dans ce cas le volume du gaz est très sensible à la pression et la température et il n'est pas possible de négliger sa variation.

$\frac {dp}{dT} = \frac {L}{T.V_{gaz}}~$

Si l'on considère que le gaz se comporte comme un gaz parfait

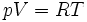$pV = RT~$ - pour une mole.

$V = \frac {RT}{p}~$

Donc

$\frac {dp}{dT} = \frac {L.p}{RT^2}~$

$\frac {dp}{p} = \frac {L}{R} \frac {dT}{T^2}~$

Intégrons

$\int_{p_{ref}}^{p_{eq}}\frac {dp}{p} = \frac {L}{R}\int_{T_{ref}}^{T_{eq}} \frac {dT}{T^2}~$

$Ln \frac {p_{eq}}{p_{ref}} = \frac {L}{R}\left(\frac {1}{T_{ref}} - \frac {1}{T_{eq}}\right)~$

D'où

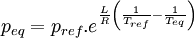
: $p_{eq} = p_{ref}.e^{ \frac {L}{R}\left(\frac {1}{T_{ref}} - \frac {1}{T_{eq}}\right)}~$

Cette relation permet d'obtenir les courbes de pression d'équilibre correspondant aux branches de vaporisation et de sublimation sur le diagramme de Clapeyron.

Diagramme de Clapeyron

Exemple de diagramme de phase de l'eau où les courbes sont déduites de la relation de Clapeyron

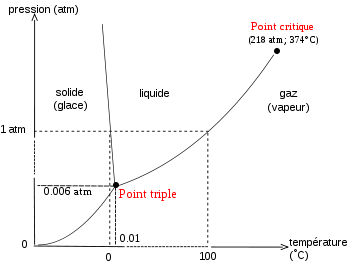
Les trois courbes de fusion-solidification, sublimation-condensation, vaporisation-condensation, décrites par les relations de Clapeyron intégrées, sont représentées sur le diagramme de Clapeyron Péq = f (Téq). Ces trois branches se rejoignent au point triple qui est le seul point où coexistent les trois états physiques, liquide-solide-gaz, du corps pur. La branche de vaporisation se termine au point critique; point au delà duquel le liquide et le gaz ne peuvent plus être différenciés.

Sur la figure de gauche est reportée une représentation schématique du diagramme de Clapeyron de l'eau, présentant les principales caractéristiques de ce diagramme; l'échelle de grandeur n'étant pas respectée. La particularité exceptionnelle concerne la pente négative de la branche de fusion-solidification, accentuée pour être visible sur ce schéma. L'eau est en effet l'un des rares corps (avec le bismuth, l'antimoine, le germanium ) à présenter un état solide moins dense que l'état liquide. Dans le cas de l'eau ce phénomène est lié à la structure cristalline de la glace dont l'édifice peu compact, est constitué de molécules d'eau reliées par des liaisons hydrogène.

Applications

Détermination d'une chaleur latente

On peut mesurer expérimentalement dans un autoclave, la température et la pression d'équilibre associée, d'un gaz au contact de son liquide. On peut alors déterminer l'évolution de la pression d'équilibre ou pression de vapeur saturante en fonction de la température. Cette étude permet la détermination de la chaleur latente de changement d'état.

Relation de Clapeyron intégrée en présence d'un gaz. On va raisonner ici sur un équilibre de vaporisation en admettant que la chaleur latente de vaporisation reste pratiquement constante sur l'intervalle de T considéré.

$Ln \frac {p_{eq}}{p_{ref}} = \frac {L}{R}\left(\frac {1}{T_{ref}} - \frac {1}{T_{eq}}\right)~$

$Ln p_{eq} = \left( Ln p_{ref} + \frac {L}{R.T_{ref}}\right) - \frac {L}{R}.\frac{1}{T_{eq}}~$

$\left( Ln p_{ref} + \frac {L}{R.T_{ref}}\right)= Constante~$

d'où

$Ln p_{eq} = - \frac {L}{R}.\frac{1}{T_{eq}} + Cte~$

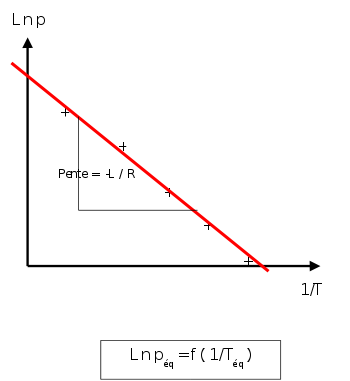
Si l'on trace le graphe : 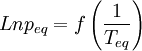$Ln p_{eq} = f \left(\frac{1}{T_{eq}}\right) ~$ on obtient une droite de pente négative

$pente = - \frac{L}{R}~$

La détermination graphique de cette pente permet le calcul de la chaleur latente:

$L = - pente.R~$

Problème pratique

La relation intégrée dans le cas de la fusion de la glace est appliquée pour savoir s'il y aura changement de phase ou non selon les conditions de pression et de température. Par exemple, elle est souvent utilisée pour expliquer ce qui permet le patinage sur glace: l'augmentation de pression du patineur fait fondre une mince couche de glace sous le patin ce qui permet la glisse.

Si T2 = 271K (-2 °C), utilisons la relation de Clausius-Clapeyron, pour calculer le changement de pression nécessaire:

$\Delta p = p_2 - p_{ref} = \frac {L_{fus}}{\Delta V} Ln \left(\frac{T_2}{T_{ref}}\right)~$

En utilisant les valeurs:

L = 3,34*10⁵ J/kg, Tref = 273K,

Δ V

= -9,05 *10^-5 m³/kg

nous obtenons

Δ p

= 27,2 MPa.

Météorologie

En météorologie, la relation de Clausius-Clapeyron est utilisée couramment dans les diagrammes thermodynamiques comme les téphigrammes, Skew-T et émagrammes pour le calcul des énergies de changement de phases de l'eau atmosphérique. Sur un tel diagramme de pression versus température (P-T), la ligne séparant les deux phases est connue comme la courbe de coexistence: dP/dT.

Ce qui est surtout important en météorologie est la pression de saturation de la vapeur d'eau

''' e s'''

et la relation devient alors:

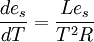$\frac {d e_s}{dT} = \frac {L e_s} {T^2 R}$ où

R

est la constante des gaz parfaits.

Notes et références de l'article

↑ Par exemple le volume molaire de l'eau liquide est voisin de 18 mL alors que celui de l'eau gaz est voisin de 22400 mL.

Paul Arnaud, Cours de chimie physique, Dunod (1990).

P.W. Atkins, Physical Chemistry, third ed., Oxford University Press, 1985.

Voir aussi

Liens externes

Le diagramme des phases de l'eau par Météo-France

Portail de la physique
Portail de la météorologie

Ce document provient de « Formule de Clapeyron ».

Catégories : Thermodynamique | Thermodynamique atmosphérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Clausius-Clapeyron de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Clausius-Clapeyron — Die Clausius Clapeyron Gleichung wurde 1834 von Benoit Clapeyron entwickelt und später von Rudolf Clausius aus den Theorien der Thermodynamik abgeleitet. Sie ist eine Spezialform der Clapeyron Gleichung. Über sie lässt sich der Verlauf der… … Deutsch Wikipedia
Clausius–Clapeyron relation — The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, who defined it sometime after 1834, is a way of characterizing a discontinuous phase transition between two phases of matter. On a pressure–temperature… … Wikipedia
Clausius-Clapeyron relation — The Clausius Clapeyron relation, named after Rudolf Clausius and Émile Clapeyron, is a way of characterizing the phase transition between two phases of matter, such as solid and liquid. It is commonly learned in class. On a pressure temperature… … Wikipedia
Clausius-Clapeyron-Gleichung — Die Clausius Clapeyron Gleichung wurde 1834 von Benoit Clapeyron entwickelt und später von Rudolf Clausius aus den Theorien der Thermodynamik abgeleitet. Sie ist eine Spezialform der Clapeyron Gleichung. Über sie lässt sich der Verlauf der… … Deutsch Wikipedia
Clausius-Clapeyron-Gleichung — Clau|si|us Cla|pey|ron Glei|chung [ klapɛ rɔ̃ ; nach R. J. E. Clausius u. dem frz. Ingenieur B. P. E. Clapeyron (1799–1864)]: eine die Abhängigkeit des Dampfdrucks (p) von der Temperatur (T) bei Phasenübergängen beschreibende Gleichung: dp/dT =… … Universal-Lexikon
Clausius-Clapeyron equation — Klauzijaus ir Klapeirono lygtis statusas T sritis fizika atitikmenys: angl. Clausius Clapeyron equation vok. Clausius Clapeyronsche Gleichung, f rus. уравнение Клаузиуса Клапейрона, n pranc. équation de Clausius Clapeyron, f … Fizikos terminų žodynas
Clausius-Clapeyron equation — Klapeirono ir Klauzijaus lygtis statusas T sritis Energetika apibrėžtis Lygtis, reiškianti grynos medžiagos slėgio ir termodinaminės temperatūros tarpusavio priklausomybę esant faziniams virsmams (pvz., virimas, lydymasis ir kt.). atitikmenys:… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
clausius-clapeyron — clau·si·us clapeyron … English syllables
clausius-clapeyron equation — |klȯzēəs.ˈklapāˌrōn , ˌrän noun Usage: usually capitalized both Cs Etymology: after Rudolf J. E. Clausius died 1888 German mathematical physicist and B. P. E. Clapeyron died 1864 French engineer : the Clapeyron equation as modified for liquid… … Useful english dictionary
Equation de Clausius-Clapeyron — Formule de Clapeyron Pour les articles homonymes, voir Clapeyron. La formule de Clapeyron ou relation de Clausius Clapeyron est une relation permettant de définir l évolution de la pression d équilibre en fonction de la température d équilibre au … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Clausius-Clapeyron

Formule de Clapeyron

Sommaire

Expression différentielle de la formule de Clapeyron

Établissement de la formule de Clapeyron

Relations de Clapeyron intégrées

Diagramme de Clapeyron