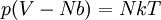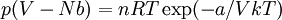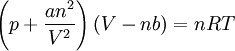- Équation de Clausius
-
Gaz réel
Un gaz réel, en physique, qualifie un gaz qui se trouve dans une condition qui n'est plus décrite de façon satisfaisante par le modèle du gaz parfait. Afin de décrire correctement le comportement du gaz réel, il est nécessaire de rajouter des termes correctifs au modèle du gaz parfait, afin de tenir compte par exemple des interactions entre particules ou encore du volume non négligeable des molécules.
Ces termes correctifs, qui dépendent fortement de la nature du gaz, sont généralement à prendre en compte aux pressions élevées. En effet aux basses pressions tous les gaz tendent à avoir un comportement de gaz parfait.
Sommaire
Gaz et paramètres
En théorie
On considère un corps pur dans son état gazeux à l'équilibre thermodynamique. Pour modéliser le comportement de cette phase gazeuse, on dispose de plusieurs modèles :
- Le modèle du gaz parfait, valable pour les basses pressions et pour tous les gaz
- Le modèle du gaz réel, qui y apporte des termes correctifs, pour les pressions plus élevées.
Le comportement du gaz est décrit par une équation d'état, qui relie entre eux tous les paramètres du gaz. Pour un corps pur, un état d'équilibre thermodynamique est alors caractérisé par deux variables macroscopiques quelconques (voir la notion de variance), parmi :
- V, volume occupé par le gaz.
- p, pression du gaz, en Pa
- T, température du gaz, en K
- U, énergie interne du gaz, en J
- S, l'entropie du gaz, en J.K − 1
- Et évidemment : toute combinaison utile de ces variables :
- pV
- H=U+pV, enthalpie
- F=U-TS, énergie libre
- G=H-TS, enthalpie libre
En pratique
On pose G(p,T,N) = N G(p,T,1), où G(p,T,1) est l'enthalpie libre moléculaire (on peut préférer l'enthalpie libre molaire G(T,p,NA))
La connaissance de G permet de tout connaître sur le gaz. Or on arrive assez bien à construire expérimentalement les tables thermodynamiques de G(p,T,N) en fonction de p et T. La physique dispose ainsi de tables pour chaque corps pur.
De plus, comme le comportement à basse pression du gaz réel s'approche de celui du gaz parfait, on peut associer à tout corps pur un gaz parfait de même capacité calorifique à pression constante
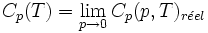
De ce fait, les tables thermodynamiques G(p,T,N) donnent souvent les correctifs à apporter à la valeur bien déterminée G(p,T,N,gaz-parfait-associé).
Équations d'état d'un gaz réel f(p,V/n,T)=1
On considère par la suite un système de N molécules de gaz réel à l'équilibre thermodynamique.
Gaz parfait
Souvent on choisit de fixer les paramètres p et T pour définir un état d'équilibre thermodynamique. Alors V/N est fixé. L'équation d'état du gaz parfait est la relation :
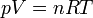
Où p est la pression du gaz, V son volume, n la quantité de matière du gaz, R la Constante des gaz parfaits et T la température absolue. Si la pression est en Pascal, le volume en m3 et la température en Kelvin, on donne alors à la constante des gaz parfaits la valeur 8,314 J/mol/K.Tous les gaz tendent vers ce comportement pour les basses pressions.
Mais comme tout gaz se liquéfie, aucun gaz réel ne peut être gaz parfait dans toute l'étendue des valeurs p et T. Il existe une ligne p = pS(T), dite ligne de pression de vapeur saturante, suivant laquelle le gaz commence à se liquéfier. On est alors bien loin du comportement du gaz parfait. On se ramène alors à un problème de transition de phase (voir l'article Diagramme de phase pour plus de détail).
Gaz de Clausius
L'équation d'un gaz de Clausius s'écrit
Où b = Volume d'une molécule
Elle rend compte du fait qu'à température fixée, un gaz n'est pas indéfiniment compressible. En d'autres mots, si la pression p tend vers l'infini, le volume V tend vers le seuil incompressible Nb, appelé covolume. L'origine de ce terme correctif est donnée dans l'article pression cinétique.
Gaz de Dieterici
L'équation d'état d'un gaz de Dieterici est
Gaz de Van der Waals
Le thermodynamicien Van der Waals a établi en 1870 une « assez bonne » représentation du comportement des gaz par l'équation d'état (qui porte aujourd'hui son nom):
Le terme nRT/V est l'habituelle pression cinétique. Van der Waals l'a diminuée d'un terme
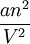qui représentait dans sa thèse les forces d'attraction entre molécules : on appelle dorénavant ces forces les forces de Van der Waals.La grande puissance de cette équation est qu'avec la règle du palier de Maxwell, elle permet une description thermodynamique de l'état gazeux et de l'état liquide à l'aide d'une unique équation. Elle représentait pour l'époque une avancée spectaculaire.
Bien qu'elle soit toujours enseignée, cette équation d'état a montré ses limites ; et l'informatique aidant, on préfère se référer aux tables de correction par rapport au gaz parfait associé, plutôt qu'au gaz de Van der Waals associé (pour en savoir plus , cf équation d'état).
Surface caractéristique
G(p,T) est une fonction caractéristique du système, en ce sens que sa connaissance implique la connaissance totale du système grâce aux relations entre les grandeurs (voir fonction caractéristique). C'est une fonction de 2 variables, donc est représentée par une surface.
U(V,S) est aussi une surface caractéristique d'un corps pur.
Les transformations de Legendre permettent alors d'établir que H(p,S) et F(V,T) en sont aussi.
Il existe encore d'autres fonctions caractéristiques si on prend d'autres paramètres : fonctions de Massieu, fonctions de Gouy...
Mélange de gaz réels
C'est un vrai casse-tête, car quand on mélange un gaz A avec un gaz B, on ne connaît rien de son équation d'état : il faudrait en toute rigueur refaire toutes les mesures : par exemple pour l'air vers 90K ! Heureusement, vers les basses pressions et hautes températures, le mélange se comporte souvent comme le mélange de gaz parfaits, ce qui permet d'avoir un comportement simple.
Ce problème a des applications directes : il se pose dans tous les bateaux méthaniers (car il y a toujours du propane et/ou du butane, mélangé au méthane). L'Institut français du pétrole (IFP) a consacré d'innombrables études à ce problème.
Voir aussi
Portail de la chimie
Portail de la physique
Catégorie : Gaz
Wikimedia Foundation. 2010.
