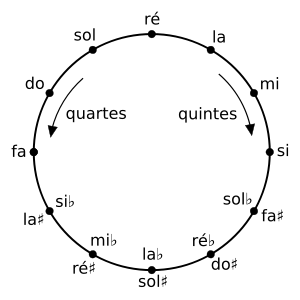
- Cercle des quintes
-
Cycle des quintes
Acoustique musicale - Note de musique
- Harmonique
- Intervalle
- Consonance
- Cycle des quintes
Gamme musicale Gammes et tempéraments Mesure des intervalles En théorie de la musique, le cycle des quintes (ou cercle des quintes) est un espace géométrique imaginaire décrivant les relations entre les 12 degrés de la gamme tempérée, représentées par des intervalles de quintes. La première description du cycle des quintes date de 1728, par Johann David Heinichen, dans son traité « Der Generalbass in der Composition ».
Sommaire
Structure
Cycle des quintes et des quartes
Dans la gamme tempérée, en commençant par une note quelconque et en montant par intervalles de quintes justes, on passe par toutes les notes de la gamme chromatique tempérée avant de retomber sur la note initiale.
Comme cet espace est circulaire, il est aussi possible de le parcourir en sens inverse : l'intervalle entre chaque note est alors une quarte juste (le renversement de la quinte juste). Le cycle des quintes est donc aussi le cycle des quartes.
Utilisation
Cycle des quintes représentant les tonalités majeuresCe cercle est souvent utilisé pour représenter les relations entre les échelles diatoniques. Sur le schéma à droite, en choisissant une note pour tonique, le chiffre à l'intérieur du cercle indique le nombre de dièses ou de bémols de l'armure correspondante.
Par exemple, la gamme de la majeur aura trois dièses dans son armure ; celle de fa majeur aura un bémol. Pour les tonalités mineures, il suffit de tourner les notes de 3 crans dans le sens inverse des aiguilles d'une montre : le bécarre (zéro dièses ou bémols) coïncide alors avec le la. Ainsi, la gamme de mi mineur aura un dièse.
Dans les systèmes d'accord non tempérés, la suite des quintes ne forme pas un cycle, on utilise alors une spirale plutôt qu'un cercle pour la représenter.
(en) Cycle des quintes sur le pianoNotes
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Circle of fifths ».
Voir aussi
Articles connexes
Liens externes
Portail de la musique
Catégorie : Théorie de la musique
Wikimedia Foundation. 2010.
