Centre instantané de rotation

Centre instantané de rotation

Le centre instantané de rotation (CIR) est un terme utilisé en mécanique classique et plus particulièrement en cinématique pour désigner le point autour duquel tourne un solide à un instant donné par rapport à un repère de référence.

Sommaire

Définition

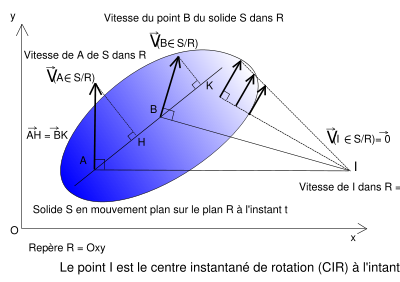
À l'instant t, I est le centre instantané de rotation du solide S dans le repère R défini par les axes Ox et Oy.

Lorsqu'un solide isolé au sens mécanique du terme, se déplace suivant une trajectoire comprise dans un plan, le CIR se définit comme le point où le vecteur vitesse est nul.

Le CIR se situe sur la perpendiculaire à chaque vecteur vitesse du solide isolé passant par le point d'application de ce dernier.

Lorsque le solide isolé se déplace uniquement en translation dans un plan, le CIR est projeté à l'infini.

Le torseur cinématique réduit au CIR est :

\{\mathcal{V}_{\mathrm{S/R}} \} = \begin{matrix} \\ \ \end{matrix}_{\mathrm{CIR}} \begin{Bmatrix} \ \vec \Omega_{\mathrm{S/R}} \\ \ \vec 0 \end{Bmatrix}_{\mathrm{O}, x, y, z}

Exemple des danseuses de cancan

Danseuses de French cancan vues de haut

L'illustration représente des danseuses de cancan vues de dessus. Si on considère que l'ensemble des cinq danseuses est un solide isolé au sens mécanique du terme, on peut dire que le centre instantané de rotation est la danseuse centrale, puisqu'elle n'a pas de vitesse relative contrairement à ses compagnes qui ont une vitesse proportionnelle à leur éloignement du centre.

Justification

Sur un court instant, le mouvement d'une bielle (bas) dans un système manivelle-bielle-piston est équivalent à une rotation autour du CIR (haut)

Considérons une pièce ayant un mouvement plan quelconque, par exemple le mouvement d'une bielle. Si l'on prend une photographie, on a un flou en raison du mouvement : les points « filent », et les segments de droite générés par les points sont une image des vecteurs vitesse.

Si la bielle était en rotation autour de son CIR, on obtiendrait une photo semblable, avec le même flou. Sur un très court instant — le temps de pose de la photographie —, les deux mouvements sont équivalents.

De manière plus rigoureuse : le torseur cinématique d'un solide en mouvement plan dans le plan (Oxy ) réduit à un point quelconque A s'écrit :

\{\mathcal{V}_{\mathrm{S/R}} \} = \begin{matrix} \\ \ \end{matrix}_{\mathrm{A}} \begin{Bmatrix} 0 & v_x(\mathrm{A}) \\ 0 & v_y(\mathrm{A}) \\ \omega_z & 0 \end{Bmatrix}_{\mathrm{O}, x, y, z}

c'est un glisseur puisque \vec{\mathrm{V}}(\mathrm{A}) et \vec{\Omega} sont orthogonaux. Il existe donc un point B tel que \vec{\mathrm{V}}(\mathrm{B}) = \vec{0}. d'après la propriété d'équiprojectivité, on a

\vec{\mathrm{V}}(\mathrm{B})= \vec{0} = \vec{\mathrm{V}}(\mathrm{A})+\overrightarrow{\mathrm{BA}} \wedge \vec{\Omega}.

Si l'on note (X, Y, 0) les composantes de \overrightarrow{\mathrm{BA}}, on a alors

\left \{ \begin{matrix} \mathrm{X} = v_y/\omega_z \\ \mathrm{Y} = -v_x/\omega_z \end{matrix}\right .

si ωz n'est pas nul, alors le point B existe et est unique ; il est appelé centre instantané de rotation.

Utilisation du CIR dans un problème de cinématique plane

Considérons un mouvement plan qui n'est pas une mouvement de translation. Durant un court instant, tout se passe comme si le solide était en mouvement de rotation autour de son CIR. On peut alors appliquer les relations établies dans le cas des mouvements de rotation, et en particulier la notion de triangle des vitesses. Cela permet de déterminer le vecteur vitesse en un point quelconque du solide, à condition de connaître :

  • le vecteur vitesse en un point ;
  • la position du CIR.

La méthode est une alternative à la méthode de l'équiprojectivité.

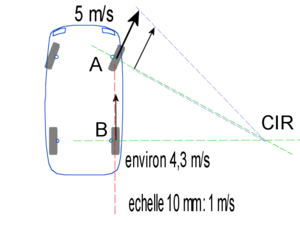
Application à une voiture dans un virage

Prenons l'exemple d'une voiture en virage, dont on connaît la direction, le sens, le point d'application et l'intensité (5 m/s) du vecteur vitesse de la roue avant. On connaît également la direction, le point d'application et le sens de la roue arrière. Les points A et B sont les centres des roues et respectivement les points d'application de leur vecteur vitesse.

L'objectif est de déterminer l'intensité du vecteur vitesse de la roue arrière.

Résolution graphique grâce au CIR :

  1. On choisit une échelle des vitesses, par exemple 10 mm pour 1 m/s ;
  2. On place le vecteur vitesse de la roue avant au point A ;
  3. On trace (en rouge) la direction du vecteur vitesse de la roue arrière au point B ;
  4. Le CIR se situe sur une droite passant par le point d'application des vecteurs vitesse et perpendiculaire à ces derniers  : on trace donc les traits verts, et on déduit le CIR ;
  5. On mesure le segment [CIR B] et on reporte la mesure sur le segment [CIR A] trait bleu ;
  6. On trace une droite passant par le CIR et par l'extrémité du vecteur vitesse associé au point A ;
  7. On trace un segment perpendiculaire à [CIR A] passant par le mesure reportée sur [CIR A] et coupant le segment passant par CIR et par l'extrémité de \vec V_{\mathrm{A}} ;
  8. On mesure ce dernier segment et en fonction de l'échelle on trouve l'intensité du vecteur vitesse \vec V_{\mathrm{B}}.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Centre instantané de rotation de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Centre Instantané De Rotation — Le centre instantané de rotation (CIR) est un terme utilisé en mécanique classique et plus particulièrement en cinématique pour désigner le point autour duquel tourne un solide à un instant donné par rapport à un repère de référence. Sommaire 1… …   Wikipédia en Français

  • Centre Instantané de Rotation — Le centre instantané de rotation (CIR) est un terme utilisé en mécanique classique et plus particulièrement en cinématique pour désigner le point autour duquel tourne un solide à un instant donné par rapport à un repère de référence. Sommaire 1… …   Wikipédia en Français

  • Centre instantane de rotation — Centre instantané de rotation Le centre instantané de rotation (CIR) est un terme utilisé en mécanique classique et plus particulièrement en cinématique pour désigner le point autour duquel tourne un solide à un instant donné par rapport à un… …   Wikipédia en Français

  • Centre instantané de rotation — ● Centre instantané de rotation point (s il existe) où la vitesse est nulle dans un mouvement plan sur plan …   Encyclopédie Universelle

  • centre instantané de rotation — akimirkinis sukimosi centras statusas T sritis fizika atitikmenys: angl. instantaneous center of rotation vok. Momentandrehzentrum, n rus. мгновенная точка вращения, f pranc. centre instantané de rotation, m …   Fizikos terminų žodynas

  • instantané — instantané, ée [ ɛ̃stɑ̃tane ] adj. • 1604; de instant, sur le modèle de momentané 1 ♦ Qui ne dure qu un instant. ⇒ 1. bref. « Des visions instantanées, rapides » (Fromentin). 2 ♦ Qui se produit en un instant, soudainement. ⇒ immédiat. Réponse,… …   Encyclopédie Universelle

  • centre — [ sɑ̃tr ] n. m. • 1275; lat. centrum, gr. kentron I ♦ 1 ♦ Point intérieur (d un cercle, d une sphère) équidistant de tous les points du cercle, de la sphère. Le centre d un disque. Le centre de la Terre. ♢ Centre de symétrie : point tel que tous… …   Encyclopédie Universelle

  • Rotation uniforme — Mouvement circulaire uniforme Le mouvement circulaire uniforme caractérise le déplacement d un point matériel dont la trajectoire dans le référentiel considéré est un cercle et dont la vitesse est constante en valeur (et non en direction :… …   Wikipédia en Français

  • rotation — [ rɔtasjɔ̃ ] n. f. • 1486, repris fin XVIIe; lat. rotatio 1 ♦ Mouvement d un corps qui se déplace autour d un axe (matériel ou non), au cours duquel chaque point du corps se meut avec la même vitesse angulaire. ⇒ giration. Rotation de la Terre.… …   Encyclopédie Universelle

  • Vitesse de rotation — Vitesse angulaire Pour les articles homonymes, voir pulsation (homonymie). En physique, et plus spécifiquement en mécanique, la vitesse angulaire ω, aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. Elle s… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”