Cinématique graphique

La cinématique graphique désigne les méthodes graphiques de résolution de problèmes cinématiques. Ce sont des méthodes

• de mécanique newtonienne ;
• pour l'étude des solides ;
• et pour les problèmes plans, c'est-à-dire lorsqu'il existe un plan Π tel que pour tout point M du solide, la distance de M à Π reste constante ; on prend en général pour Π le plan (O, x, y ).

Les méthodes de cinématique graphique consistent à mesurer des longueurs sur un dessin, parfois appelé « épure ». Ces longueur peuvent correspondre à des distances ou bien à des vitesses (représentation graphique de vecteurs vitesse). Elles permettent la résolution de problèmes sans calculs autres que les facteurs d'échelle ; ce sont donc des méthodes adaptées aux situations où l'on n'a pas accès à des moyens de calcul, ainsi qu'à l'enseignement technique et technologique.

Tracé de trajectoire

Guidage de suspension par deux biellettes

Schéma de la suspension

Schéma cinématique

Tracé de la trajectoire (épure) ; traits de construction pour la position 6

En cinématique analytique, la trajectoire — supposée plane, dans le plan (O, x, y ) — d'un point d'un solide est décrite par une équation cartésienne y = ƒ(x ) ou bien par une équation paramétrique (x(t ), y(t )). En cinématique graphique, on détermine la courbe par construction à la règle et au compas.

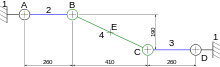
En effet, un solide étant considéré comme indéformable, la distance entre deux points donnés ne varie pas. Si l'on connaît la trajectoire de deux points A et B du solide, alors :

• on place des points équitablement répartis sur la trajectoire de A, et on les numérote A₀, A₁, A₂, … ;
• avec un compas, on détermine les points B₀, B₁, B₂, … : on place la pointe sur A_i et l'on regarde là où l'arc de rayon AB coupe la trajectoire de B ;
• on peut ainsi connaître la i-ième position de n'importe quel point C (en reportant les distances AC et BC depuis les points A_i et B_i).

On part des liaisons cinématiques de la pièce concernée avec le bâti de la machine (ou la pièce de référence) :

• les points des pièces en liaison pivot avec le bâti ont une trajectoire circulaire ;
• les points des pièces en liaison glissière avec le bâti ont une trajectoire rectiligne.

Si une pièce repérée 2 n'est pas en liaison directe avec le bâti, mais est en liaison pivot au point A avec une pièce rep. 1 elle-même en liaison avec le bâti rep. 0, alors on connaît la trajectoire du centre A de la liaison :

par rapport à 0, la trajectoire du point A de la pièce 2 est la même que la trajectoire du point A de la pièce 1, ce que l'on note T_A∈2/0 = T_A∈1/0.

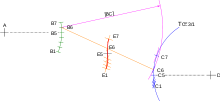
Les figures ci-contre indiquent la démarche pour un exemple concret : pour une suspension de train, on détermine la trajectoire de l'axe E de la roue rep. 4 par rapport à la voiture rep. 1 :

• les bielles rep. 2 et rep. 3 sont en liaison pivot avec la voiture, donc les trajectoires T_B∈2/1 et T_C∈3/1 sont des arcs de cercle de centre respectivement A et D ;
• on a T_B∈4/1 = T_B∈2/1 et T_C∈4/1 = T_C∈3/1 ;
• on place 7 point répartis équitablement sur T_B∈4/1 : B₁ à B₇ ;
• en reportant la longueur BC, on détermine les points C₁ à C₇ correspondant ;
• E est le milieu de [BC], on détermine donc la position des points E₁ à E₇.

Détermination des vitesses des points d'un solide

Dans un mécanisme, on a un actionneur (moteur, vérin), qui fournit l'effort, et un effecteur, qui fait le travail (outil). Entre les deux, on peut avoir une ou plusieurs pièces, et notamment un levier qui a pour but d'amplifier l'effort ou bien d'amplifier le mouvement.

le cahier des charges indique quelle doit être la vitesse de l'effecteur, soit en termes de fréquence (cadence de production), soit en termes de vitesse minimale (efficacité requise) ou maximale (protection des biens et des personnes). Mais ce que l'on commande, c'est la vitesse de l'actionneur. Il est donc important de pouvoir relier les deux. En particulier, s'il y a une pièce entre l'actionneur et l'effecteur, il faut pouvoir déterminer la vitesse d'un point connaisant la vitesse de l'autre point.

Dans le cas d'un solide indéformable, le champ des vecteurs vitesse est équiprojectif. Cela donne des propriétés géométriques particulières.

Solide en translation

Pour un solide en translation, le champ des vecteurs vitesse est uniforme. Il n'y a donc pas à proprement parlé de détermination graphique, si l'on connaît le vecteur vitesse d'un point, tous les points du solide ont le même.

Solide en rotation autour d'un axe fixe dans le référentiel

Champ des vecteurs vitesse pour une solide en rotation

Cas d'un point B hors de (OA)

On considère un solide en rotation autour d'un axe fixe qui est perpendiculaire au plan (O, x, y ) (hypothèse de problème plan). L'axe se résume donc à un centre de rotation O. La vitesse v des points dépend de leur distance R au centre de rotation, le coefficient de proportionnalité étant la vitesse de rotation ω :

v = R×ω

et par ailleurs, les vecteurs vitesse sont perpendiculaires au rayon (puisque tangents à la trajectoire circulaire). Donc, sur une droite donnée passant par le centre de rotation, l'extrémité des vecteurs vitesse des points de la droite forment un triangle appelé triangle des vitesses. Si l'on connaît la vitesse d'un point A, alors on détermine la vitesse des points de la droite (OA) en représentant le vecteur vitesse à une échelle donnée (par exemple 1 mm pour 1 m/s) et en traçant la droite passant par O et par l'extrémité de .

Par ailleurs, on point quelconque B va à la même vitesse que tous les points situés sur un cercle de centre O et de rayon OB ; la vitesse de B est donc la même que le point B', intersection de ce cercle et de la droite (OA).

Théorème de l'équiprojectivité

Méthode de l'équiprojectivité

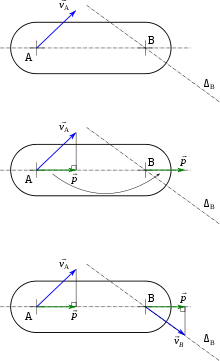
Le caractère équiprojectif du champ de vecteurs vitesse fournit deux méthodes de résolution. La première consiste simplement on considérer la définition de base : pour deux points A et B d'un solide, les projections des vecteurs vitesse et sur la droite (AB) sont égales. Cela traduit le fait que la distance AB est fixe. Si l'on connaît et la direction Δ_B de , alors :

• on trace une représentation de à une échelle donnée ;
• on projette graphiquement sur (AB), ce qui donne le vecteur projeté  ;
• on reporte en B et l'on fait la projection inverse : on tire la perpendiculaire à (AB) qui passe par l'extrémité de et on considère son intersection avec Δ_B.

Cela donne une représentation de , sa longueur donnant la valeur de .

Centre instantané de rotation

La deuxième méthode consiste à utiliser une propriété des champs équiprojectifs : si l'on n'est pas dans le cas d'une translation, il existe un point de vitesse nulle à l'instant donné et une vitesse instantanée de rotation ω associée. On se rapporte alors au cas du solide en rotation. La différence est que le centre de rotation peut varier d'un moment à l'autre.

Composition des vitesses

Composition des vitesses.

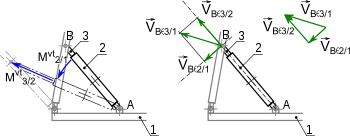
En relativité galiléenne, le changement de référentiel se traduit pour les vitesses par une somme de vecteurs : la vitesse du point A de la pièce 2 dans le référentiel lié à la pièce 0 est égale à somme de la vitesse du point A de la pièce 2 dans le référentiel lié à la pièce 1 et de la vitesse du point A de la pièce 1 dans le référentiel lié à la pièce 0 (formulation similaire à la relation de Chasles) :

.

Graphiquement, on établit cette somme en mettant les vecteurs bout-à-bout, ou bien par la méthode du parallélogramme.

Un cas typique est celui du vérin : la vitesse de la tige de vérin est la somme de la vitesse de sortie de la tige, déterminée par le débit de fluide (huile ou air), et de la vitesse du corps du vérin, qui tourne pour s'adapter au déplacement des pièces liées.

Voir aussi

Articles connexes

• Statique graphique