Équiprojectivité en physique

Équiprojectivité en physique

L’équiprojectivité est la propriété fondamentale des torseurs. En physique, on se limite aux champs de vecteurs dans l'espace affine ℝ3, c'est-à-dire l'espace réel muni un repère orthonormé.

Sommaire

Définition

Cas général

Si l'on considère un champ de vecteurs \vec{\mathcal{M}}, appelés moments, alors le champ de vecteurs moment est équiprojectif si pour deux points quelconques P et Q

\vec{\mathcal{M}}(\mathrm{P}) \cdot \overrightarrow{\mathrm{PQ}} = \vec{\mathcal{M}}(\mathrm{Q}) \cdot \overrightarrow{\mathrm{PQ}}.
Article détaillé : Champ équiprojectif.

Cas du champ des vecteurs vitesse

Illustration de l'équiprojectivité du champ des vecteurs vitesse.

Considérons le champ des vecteurs vitesse des points d'un solide, \vec{v}. Si le solide est indéformable, alors les points ne s'éloignent pas ni ne se rapprochent. Donc, si l'on considère deux points O et M, le segment [OM] garde la même longueur. Il en résulte que la projection de \vec{v}(\mathrm{O}) et de \vec{v}(\mathrm{M}) sont identiques, soit d'après la définition du produit scalaire :

\vec{v}(\mathrm{O}) \cdot \overrightarrow{\mathrm{OM}} = \vec{v}(\mathrm{M}) \cdot \overrightarrow{\mathrm{OM}}.

Le champ des vecteurs vitesse est donc équiprojectif.

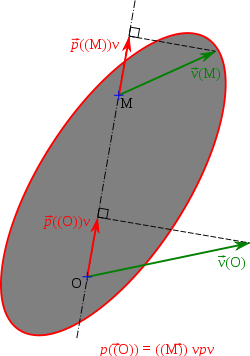
Cette propriété fournit une méthode de résolution graphique en cinématique :

  • si l'on connaît le vecteur vitesse \vec{v}(\mathrm{O}) d'un point O de l'objet, par exemple point en contact avec un actionneur (extrémité de tige d'un vérin, dent d'engrenage) ;
  • si l'on connaît la direction \Delta_{\vec{v}(\mathrm{M})} du vecteur vitesse d'un point M de l'objet, par exemple point en contact avec un dispositif de guidage (liaison pivot, liaison glissière) ;
  • alors
    1. on détermine la projection de \vec{v}(\mathrm{O}) sur (OM),
    2. on reporte ce segment en M,
    3. on fait la projection inverse de ce segment sur \Delta_{\vec{v}(\mathrm{M})}, ce qui donne \vec{v}(\mathrm{M}).

La méthode est une alternative à la méthode du centre instantané de rotation.

Vecteur résultante

Si le champ \vec{\mathcal{M}} est équiprojectif, alors il existe un vecteur \vec{\mathcal{R}} appelé résultante tel que

\vec{\mathcal{M}}(\mathrm{P})=\vec{\mathcal{M}}(\mathrm{Q})+\overrightarrow{\mathrm{PQ}} \wedge \vec{\mathcal{R}}.

On voit en effet que \overrightarrow{\mathrm{PQ}} \wedge \vec{\mathcal{R}} est orthogonal à \overrightarrow{\mathrm{PQ}}, donc que ce terme s'annule lors du produit scalaire avec \overrightarrow{\mathrm{PQ}}. Le torseur est désigné par son vecteur résultante \vec{\mathcal{R}} et son champ de vecteurs \vec{\mathcal{M}}, appelé quant à lui champ de vecteurs moment.

Ainsi, si l'on connaît le vecteur résultante et un vecteur moment en un point, on est capable de déterminer le vecteur moment en tout point. Ceci est utilisé en mécanique.

Cinématique

Dans le cas du champ des vecteurs vitesse \vec{\mathrm{V}}, la résultante est le vecteur vitesse de rotation \vec{\Omega}. On a alors

\vec{\mathrm{V}}(\mathrm{O})=\vec{\mathrm{V}}(\mathrm{M})+\overrightarrow{\mathrm{OM}} \wedge \vec{\Omega}.

Ceci justifie la méthode de résolution graphique avec le centre instantané de rotation (CIR).

Statique

Le vecteur moment par rapport à un point P d'une force \vec{\mathrm{F}} dont le point d'application est Q est défini par

\vec{\mathcal{M}}_{\mathrm{P}}(\vec{\mathrm{F}}) = \overrightarrow{\mathrm{PQ}} \wedge \vec{\mathrm{F}}.

On voit que le champ des vecteurs moment est un champ équiprojectif de vecteur résultante \vec{\mathrm{F}} et dont la valeur en Q est \vec{0}. Cette propriété permet de définir le torseur statique.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équiprojectivité en physique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Equiprojectivite — Équiprojectivité L’équiprojectivité est une propriété d une certaine classe de torseur dont fait partie le torseur cinématique d un solide en physique. Exemple du champ des vecteurs vitesse Illustration de l équiprojectivité du champ des vecteurs …   Wikipédia en Français

  • Équiprojectivite — Équiprojectivité L’équiprojectivité est une propriété d une certaine classe de torseur dont fait partie le torseur cinématique d un solide en physique. Exemple du champ des vecteurs vitesse Illustration de l équiprojectivité du champ des vecteurs …   Wikipédia en Français

  • Équiprojectivité — L’équiprojectivité est une propriété d une certaine classe de torseur dont fait partie le torseur cinématique d un solide en physique. Exemple du champ des vecteurs vitesse Illustration de l équiprojectivité du champ des vecteurs vitesse …   Wikipédia en Français

  • Champ équiprojectif — Dans un espace affine euclidien E, un champ de vecteurs est équiprojectif[1] si : où …   Wikipédia en Français

  • Torseur — Un torseur est un outil mathématique utilisé principalement en mécanique du solide indéformable, pour décrire les mouvements des solides et les actions mécaniques qu ils subissent de la part d un environnement extérieur. Sommaire 1 Définition 2… …   Wikipédia en Français

  • Champ equiprojectif — Champ équiprojectif Dans un espace affine euclidien E, un champ de vecteurs est équiprojectif si : où désigne le produit scalaire. Il existe alors un endomorphisme antisymétrique …   Wikipédia en Français

  • Champ Équiprojectif — Dans un espace affine euclidien E, un champ de vecteurs est équiprojectif si : où désigne le produit scalaire. Il existe alors un endomorphisme antisymétrique …   Wikipédia en Français

  • CINÉMATIQUE — La cinématique est la théorie qui, à l’intérieur de la mécanique, a pour objet la description des mouvements des systèmes matériels. Deux notions sont absolument indispensables à l’élaboration de la cinématique sous sa forme classique: celle de… …   Encyclopédie Universelle

  • Modele du solide (mecanique) — Modèle du solide (mécanique) Le modèle du solide est fréquemment utilisé en mécanique des systèmes de points matériels. Il s agit d une idéalisation de la notion usuelle de corps (à l état) solide, considéré comme absolument rigide. Sommaire 1… …   Wikipédia en Français

  • Modèle du solide (mécanique) — Le modèle du solide est fréquemment utilisé en mécanique des systèmes de points matériels. Il s agit d une idéalisation de la notion usuelle de corps (à l état) solide, considéré comme absolument rigide. Sommaire 1 Définition 2 Modèles discret et …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”