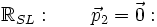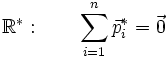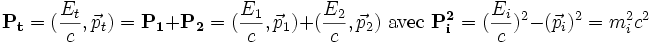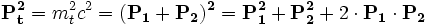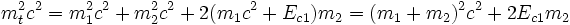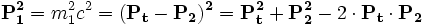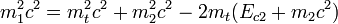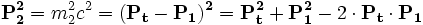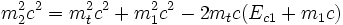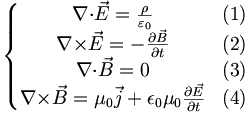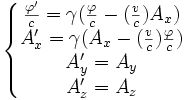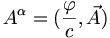- Calculs en relativité
-
Calculs relativistes
Cet article se veut volontairement calculatoire pour montrer que l'essentiel peut se déduire par le calcul des transformations de Lorentz.

Cet article de physique fait
partie de la série relativitéAvant Einstein Histoire de la physique Michelson - Lorentz Mach - Poincaré - Hilbert exp:Michelson et Morley - éther Avec Einstein Principe de relativité Principe d'équivalence c - transformation de Lorentz espace-temps - E=mc² - temps exp:pensée?-jumeaux-train relativité restreinte-générale controverse historique En physique des particules cyclotron accélérateur de particules Feynman - EQR Méta Formulaire de physique Tous les articles sur la relativité Sommaire
Les transformations de Lorentz
Soient deux référentiels
 et
et  en translation rectiligne l'un par rapport à l'autre sur des axes parallèles, avec une vitesse relative v selon l'axe Ox. Lorsque l'on passe du premier référentiel au second, les coordonnées sont liées par la transformation de Lorentz :
en translation rectiligne l'un par rapport à l'autre sur des axes parallèles, avec une vitesse relative v selon l'axe Ox. Lorsque l'on passe du premier référentiel au second, les coordonnées sont liées par la transformation de Lorentz :-
 avec
avec 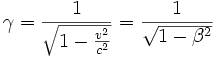 et
et 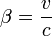
Les transformations inverses
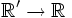 qui donnent les coordonnées dans R en fonction des coordonnées dans R' s'en déduisent en résolvant le système de deux équations à deux inconnues
qui donnent les coordonnées dans R en fonction des coordonnées dans R' s'en déduisent en résolvant le système de deux équations à deux inconnues  Il suffit de changer le signe de la vitesse :
Il suffit de changer le signe de la vitesse : Ceci est la façon matricielle d'écrire une transformation de Lorentz.
Ceci est la façon matricielle d'écrire une transformation de Lorentz.Vous pouvez constater que si vous remplacez x' et t' par leurs expressions données au-dessus en fonction de x et t, vous obtenez x = x et t = t ce qui signifie que les formules ci-dessus sont inverses l'une de l'autre ; les mathématiciens expriment cela en disant que cette propriété est une des propriétés requises pour que les transformations de Lorentz forment un groupe, la principale conséquence étant que la composition de deux transformations de Lorentz est une transformation de Lorentz. On verra dans le paragraphe relatif à la composition des vitesses une utilisation du groupe de Lorentz.
Presque tout se déduit des transformations de Lorentz, ce qui fait dire que, en Relativité restreinte, il vaut mieux se fier aux résultats du calcul que de faire des raisonnements qualitatifs. Les transformations ci-dessus sont identiques aux transformations de Galilée pour les vitesses usuelles et cependant détruisent la notion du temps universel puisque celui-ci devient dépendant du référentiel : le temps varie comme la position varie. Le temps est une coordonnée pour exprimer les lois de la physique et celles-ci deviennent covariantes lorsque on les exprime avec un espace à 4 dimensions (ct, x, y, z). En remplaçant ici t par ct, on ne fait que transformer les unités de temps de façon qu'elles soient en mètres plutôt qu'en secondes.
On va ci-dessous développer une page de calculs permettant de déduire des conséquences.
La pseudonorme
On repère un évènement par les coordonnées d'un vecteur dans un repère à 4 dimensions c temps-espace
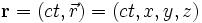
On montre facilement que :
En effet :
On note en gras la pseudonorme du vecteur à 4 dimension ou quadrivecteur:

ceci est appelé la pseudo - norme du quadrivecteur position d'un évènement repéré dans l'espace temps à 4 dimensions : On a montré mathématiquement que cette quantité ne dépendait pas du référentiel et constituait donc un invariant aux transformations de Lorentz.
La dilatation des durées
Déjà, il faut constater que au temps t' correspond une infinité de temps dans
 :
: 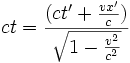
Pour simplifier , prenons t'=0:
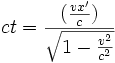
Pour le même temps t'=0 correspondent des temps t qui sont pour des x positifs dans le futur de
 et pour des x négatifs dans le passé de
et pour des x négatifs dans le passé de  !
!Soient deux référentiels,
 , et
, et  en translation rectiligne uniforme par rapport au premier référentiel suivant l'axe des x positifs à la vitesse v.
en translation rectiligne uniforme par rapport au premier référentiel suivant l'axe des x positifs à la vitesse v.Une horloge au repos dans
 au point M'(x'o,y'o,z'o), mesure deux évènements dans
au point M'(x'o,y'o,z'o), mesure deux évènements dans 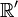 : (ct'1,x'o,y'o,z'o) et (ct'2,x'o,y'o,z'o) qui se produisent donc au même endroit et à des temps différents.
: (ct'1,x'o,y'o,z'o) et (ct'2,x'o,y'o,z'o) qui se produisent donc au même endroit et à des temps différents.Selon les transformations de changement de référentiel, x1 = γ(vt'1 + x'o) et x2 = γ(vt'2 + x'o). La durée entre deux évènements dans le référentiel
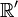 se produisant en M'(x'o,y'o,z'o) est :t'1 − t'2 La durée entre ces deux évènements dans le référentiel
se produisant en M'(x'o,y'o,z'o) est :t'1 − t'2 La durée entre ces deux évènements dans le référentiel  est :
est :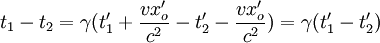
En posant τ0 = t'1 − t'2 la durée au repos, et τ = t1 − t2 la durée observée dans le référentiel
 , nous obtenons la formule dite de dilatation des durées :
, nous obtenons la formule dite de dilatation des durées :Ainsi, vu du référentiel
 par deux observateurs situés en x1 = γ(vt'1 + x'o) et x2 = γ(vt'2 + x'o)et qui ont synchronisé leurs horloges dans le référentiel
par deux observateurs situés en x1 = γ(vt'1 + x'o) et x2 = γ(vt'2 + x'o)et qui ont synchronisé leurs horloges dans le référentiel  la mesure de l'intervalle de temps n'est pas égal à celui mesuré par un observateur immobile situé en M'(x'o,y'o,z'o):
la mesure de l'intervalle de temps n'est pas égal à celui mesuré par un observateur immobile situé en M'(x'o,y'o,z'o):La quantité τ0 s'appelle temps propre . Comme
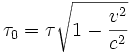 , on voit que la quantité
, on voit que la quantité 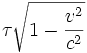 est un invariant relativiste.
est un invariant relativiste.Le facteur
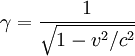 qui intervient dans la dilatation des durées, a, pour un avion, une valeur approchée de 1 + v²/2c² soit 1+10^(-10) =1.0000000001 Quelques microsecondes sur un an de vol de supersonique ! Difficile de croire à la réalisation d'une mesure de la dilatation du temps en comparant l'indication d'horloges demeurées au sol à l'indication d’horloges emportées sur un avion (cette expérience a eu lieu aux USA en 1972 de façon non probante). Néanmoins les chercheurs travaillant sur les particules produites dans les synchrotrons vivent quotidiennemnt l'effet de la dilatation du temps T= γ T'.
qui intervient dans la dilatation des durées, a, pour un avion, une valeur approchée de 1 + v²/2c² soit 1+10^(-10) =1.0000000001 Quelques microsecondes sur un an de vol de supersonique ! Difficile de croire à la réalisation d'une mesure de la dilatation du temps en comparant l'indication d'horloges demeurées au sol à l'indication d’horloges emportées sur un avion (cette expérience a eu lieu aux USA en 1972 de façon non probante). Néanmoins les chercheurs travaillant sur les particules produites dans les synchrotrons vivent quotidiennemnt l'effet de la dilatation du temps T= γ T'.Et aujourd'hui,les horloges atomiques embarquées dans les satellites des systèmes GPS sont calibrées de façon à ce que leurs indications soient compatibles avec des horloges restées sur Terre.
La contraction des longueurs
Nous nous plaçons dans les conditions évoquées au précédent paragraphe. Mesurer une longueur M1M2 revient à repérer dans un système de coordonnées les deux extrémités M1 et M2 ; Cela ne pose pas de problème si celles-ci ne bougent pas dans le temps ; par contre si elles se déplacent à la même vitesse v, il faudra repérer ces deux extrémités simultanément. Nous considérons donc une règle au repos dans
 , de longueur L0 au repos. Les coordonnées de ses extrémités sont x'1 et x'2. Les évènements de ses extrémités sont : (t',x'1,0,0) et (t',x'2,0,0), car il faut observer simultanément ces évènements dans
, de longueur L0 au repos. Les coordonnées de ses extrémités sont x'1 et x'2. Les évènements de ses extrémités sont : (t',x'1,0,0) et (t',x'2,0,0), car il faut observer simultanément ces évènements dans  .
.Considérons maintenant les évènements (t'1,x'1,0,0) et (t'2,x'2,0,0), on obtient dans
 :
:Déterminons t'2 − t'1 pour que ces évènements soient simultanés dans
 , il faut que :
, il faut que :-
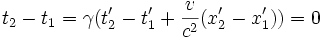 soit :
soit :
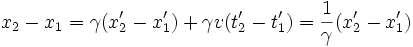
La longueur de la règle, observée dans le référentiel
 s'exprime :
s'exprime :Ainsi, la règle est plus courte dans le référentiel
 que dans le référentiel
que dans le référentiel  : la règle M1M2 en mouvement est plus courte lorsque la mesure de sa longueur est faite dans un référentiel dans lequel M1M2 est en mouvement.
: la règle M1M2 en mouvement est plus courte lorsque la mesure de sa longueur est faite dans un référentiel dans lequel M1M2 est en mouvement.Ainsi un coureur R' de 100m va s'autochronométrer avec sa montre un temps propre de T'0=10s sur une piste de L0 = 100m dans R : pour le coureur, la piste qui défile à la vitesse v sous ses enjambées ne fait pas 100 m elle est contractée L'=L0/γ ; par contre pour le juge de piste la piste est immobile par rapport à lui ; elle fait L0 = 100m en longueur propre et le temps est T=γT'0 c'est-à-dire dilaté. Le coureur et le juge ne sont d'accord ni sur le temps ni sur la distance, mais sont d'accord sur la vitesse v = L'/T'0= L0/T. Bien sûr, aux vitesses d'un coureur de 100m, toutes ces différences sont imperceptibles. Les effets relativistes ne sont perceptibles que à l'échelle nucléaire ou à l'échelle galactique.
La composition des vitesses
Nous savons dans la vie quotidienne que les vitesses s'ajoutent. Prenons un exemple concret, je prends le métro, et je marche à 5 km/h sur un tapis roulant allant dans le même sens à 4 km/h. Ma vitesse par rapport au sol est de 9 km/h. Nous allons voir comment obtenir la formule de composition des vitesses galiléenne, puis relativiste. Nous supposerons dans ce paragraphe que tous les déplacements se font parallèlement à un même axe.
Cas galiléen
Les transformations de Galilée sont :
en différenciant, on obtient :
ou encore:
le quotient donne : u = u' + v, avec
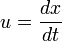 et
et 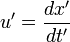 , ce qui est la loi de composition classique: les vitesses s'ajoutent.
, ce qui est la loi de composition classique: les vitesses s'ajoutent.Cas relativiste
Les transformations de Lorentz sont :
en différenciant, on obtient :
le quotient donne :
-
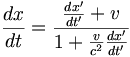 Soit :
Soit : 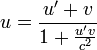 la loi de composition relativiste des vitesses : elles ne s'ajoutent pas
la loi de composition relativiste des vitesses : elles ne s'ajoutent pas
Si u' = c, alors on obtient u = c. La vitesse de la lumière est la même dans les deux référentiels.
Utilisation du groupe de Lorentz
Soit L(v) la matrice
avec
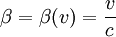 et
et 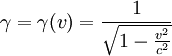 . Cette matrice, appliquée aux composantes
. Cette matrice, appliquée aux composantes 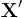 dans un référentiel
dans un référentiel  donne les composantes
donne les composantes 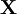 dans le référentiel
dans le référentiel  par rapport auquel
par rapport auquel  se déplace avec une vitesse v :
se déplace avec une vitesse v :Si on dispose d'un référentiel
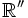 se déplaçant par rapport au référentiel
se déplaçant par rapport au référentiel  à la vitesse u', alors les relations entre les composantes
à la vitesse u', alors les relations entre les composantes 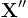 dans le référentiel
dans le référentiel 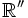 et les composantes
et les composantes 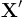 dans le référentiel
dans le référentiel  sont données par :
sont données par :On a donc :
La matrice produit L(v)L(u') n'est autre que la matrice L(u), où u est la vitesse du référentiel
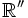 par rapport au référentiel
par rapport au référentiel  . On vérifiera que
. On vérifiera que  , et donc que
, et donc que 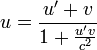 , comme plus haut.
, comme plus haut.On se reportera au paragraphe ci-dessous pour le cas plus général où les vitesses u et v ne sont pas colinéaires.
Le quadrivecteur vitesse
Transformation des vitesses
On peut calculer une vitesse en formant le rapport d'une distance par un temps :
Ce sont les transformations sur les vitesses et l'on constate que les vitesses ne s'ajoutent pas : il ne faut pas appeler ces relations en utilisant le mot 'addition' par contre
Ces relations peuvent s'écrire différemment si on calcule :
soit:
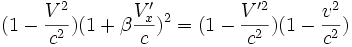
En posant
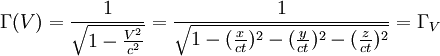 et
et 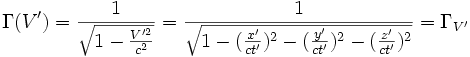 et
et 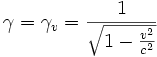 .
.s'écrit
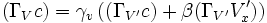 . qui est une des transformations de Lorentz si on considère le quadrivecteur
. qui est une des transformations de Lorentz si on considère le quadrivecteur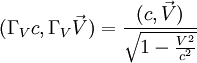 est le quadrivecteur vitesse.
est le quadrivecteur vitesse.
-
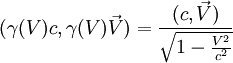 est le quadrivecteur vitesse.
est le quadrivecteur vitesse.
Utilisation des invariants:Pseudo-norme et Temps propre
considérons::
 et
et  tous deux invariants.
tous deux invariants.- cdτ = ds
En relativité restreinte, nous avons un invariant qui a pour dimension une longueur (que nous appelons longueur propre) : Nous définissons le temps propre de la manière suivante Nous obtenons :
dτ est l'accroissement de temps mesuré dans un référentiel en mouvement avec une vitesse V par rapport à un référentiel
 dans lequel l'accroissement de temps est dt. La quantité
dans lequel l'accroissement de temps est dt. La quantité 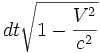 ne dépend pas du référentiel
ne dépend pas du référentiel  choisi. C'est un invariant relativiste.
choisi. C'est un invariant relativiste.Nous définissons alors naturellement la quadrivitesse :
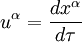
qui a une pseudo norme égale à 1
Le voyage dans le futur des autres
Ou le paradoxe des jumeaux :
- Rappelons ce paradoxe :
On considère deux jumeaux A et B. A entreprend un long voyage puis revient vers B. A est alors censé avoir vieilli moins que B. Un paradoxe est soulevé si, en se plaçant du point de vue de A, il considère que c'est B qui voyage et qui devrait avoir moins vieilli que lui. Par conséquent, il n'y a aucune raison de trouver une dilatation du temps de l'un par rapport à l'autre.
- Pour lever le paradoxe, il faut repérer où se situe une dissymétrie :
B se situe dans un référentiel inertiel
 et n'en change pas. Dans un premier temps, A se situe dans un référentiel inertiel
et n'en change pas. Dans un premier temps, A se situe dans un référentiel inertiel  se déplaçant à la vitesse v par rapport à
se déplaçant à la vitesse v par rapport à  , puis A fait demi-tour. Il change alors de référentiel inertiel et se trouve cette fois dans un référentiel inertiel
, puis A fait demi-tour. Il change alors de référentiel inertiel et se trouve cette fois dans un référentiel inertiel  se déplaçant à la vitesse -v par rapport à
se déplaçant à la vitesse -v par rapport à  .
.- La dissymétrie provient donc du fait que A change de référentiel inertiel, et pas B. Dans ce qui suit, on va illustrer par l'effet Doppler l'évolution des vies de A et de B. Nous verrons que lorsque A et B s'éloignent l'un de l'autre, l'effet Doppler des signaux qu'ils s'envoient l'un vers l'autre est identique (la fréquence des signaux est diminuée dans le même rapport). Lorsque A et B se rapprochent l'un de l'autre, il en est de même (la fréquence des signaux est augmentée dans le même rapport). Mais l'inversion de l'effet Doppler dépend uniquement de A, et B n'y joue aucun rôle. Ceci expliquera que, du point de vue de A ou de B, B a davantage vieilli que A.
On considère R' le référentiel du voyageur A qui se déplace à 3/5 c ce qui donne une dilatation du temps de
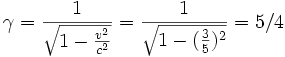
- Si T0 est la durée du voyage dans R', dans R le voyage aller a duré T1 = γT0 = 5/4 années, en parcourant vγT0= 3/5×5/4 T0 année-lumière= 3/4 T0 a.l.
(a.l. signifie année-lumière ou distance parcourue par la lumière en un an)
- Pour simplifier prenons un voyage de T0 = 1 an et pour moderniser le voyage, O et O' sont sous vidéo avec émission en continu.
- Par effet Doppler, les émissions sont reçues au ralenti avec un facteur (1+v/c) = 8/5 qui combiné avec la dilatation du temps 5/4 donne
Il faut donc à chacun, et la situation est symétrique pour B en O et A en O', le double de temps pour visionner en « direct » la vie de l'autre tant que ni l'un ni l'autre ne modifie son mouvement.
- Supposons que A s'arrète au bout d'un an, sans revenir.
-
- Point de vue de A : Il a reçu 6 mois de la vie de B au ralenti en un an de son trajet et recevra la suite de vie de B avec un retard de 3/4 d'an à un rythme normal. La dernière minute des six mois de la vie de B, visionnée au ralenti par A, a été émise 3/4 d'an plus tôt : A sait donc que B a vécu 5/4 d'année depuis son départ, ce qui est bien la durée T1 du voyage de A dans le référentiel de B.
-
- Point de vue de B : Après avoir reçu au ralenti le voyage aller de A en 2 ans, B reçoit la vie de A avec un retard de 3/4 d'an à un rythme normal. La dernière minute du voyage de A, visionnée au ralenti par B, a été émise 3/4 d'an plus tôt : B sait donc que le voyage de A a duré (dans le référentiel de B) 2 ans moins 3/4 année, soit 5/4 d'année, ce qui est bien la durée T1 du voyage de A dans le référentiel de B.
- Supposons maintenant que A en O' fasse demi tour au bout d'un an temps propre pour lui :
ERREUR : Si A fait demi-tour, on ne peut plus faire de calcul relativiste puisque sa vitesse varie nécessairement, ce qui est contraire à l' hypothèse de départ.!
-
- Point de vue de A : Il n'a alors visionné que 6 mois de la vie de B situé en O et il lui reste à recevoir ce qui est sur les 3/4 a.l qui séparent O de O', soit 3/4 ans du vécu de B en O non visionné par A situé en O', auquel il faudra ajouter la durée de vie de B pendant le voyage retour de A, soit T1 = 5/4 ans de la vie de B. A recevra donc en accéléré, en un an de son voyage retour, 2 ans de vie de B en O, ce qui est bien conforme à une réception en accéléré due au fait que le voyage retour rapproche A et O. En effet :
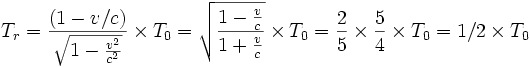
- A a donc voyagé pendant 2 ans et se retrouve avec B en O qui a vécu 6 mois + 2 ans = 2 ans et demi = 2T1.
-
- C'est l'effet dilatation du temps.
-
- Noter que A a fait demi tour dans un espace contenant des ondes qui se propagent vers B en O.
-
- Point de vue de B : En O, il reçoit pendant 2 ans le voyage aller de A en O' et lorsque A fait demi-tour, il ne le sait pas encore. Lorsqu'il reçoit l'information que A en O' a fait demi tour il y a déjà 3/4 d'an que A voyage sur le retour et A sera dans 6 mois en O : B en O reçoit ce retour d'un an de la vie de A en accéléré en ces 6 mois. B aura mis 2 ans et 6 mois pour recevoir les « 2ans » de voyage de A.
Tous les premiers de chaque mois, A et B s'envoient mutuellement le rang du mois qui commence pour eux. Dans le tableau ci-dessous, on affiche dans la colonne de gauche le rang vécu par A et qu'il envoie à B, alors que la colonne de droite affiche les messages que perçoit A de la part de B. Pendant le voyage aller, la vie de B s'affiche deux fois moins vite, alors que pendant le voyage retour, la vie de B s'affiche deux fois plus vite.
Point de vue de A Horloge de A Visionnage de la vie de B A s'éloigne de B et visionne la vie de B
au ralenti (deux fois moins vite)1 1 2 1 3 2 4 2 ... ... 10 5 11 6 12 6 A fait demi-tour.
Il se rapproche de B et visionne la vie de B
en accéléré (deux fois plus vite)13 8 14 10 15 12 ... ... 23 28 24 30 On peut procéder de même pour B. On prendra garde que A fait demi-tour au bout de 15 mois de B, mais que B ne le voit que 9 mois plus tard, le temps que le signal parvienne jusqu'à lui, donc au bout de 24 mois.
Point de vue de B Horloge de B Visionnage de la vie de A A s'éloigne de B. B visionne sa vie
au ralenti (deux fois moins vite)1 1 2 1 3 2 4 2 ... ... 22 11 23 12 24 12 B voit que A fait demi-tour.
Il se rapproche de B et B visionne sa vie
en accéléré (deux fois plus vite)25 14 26 16 27 18 28 20 29 22 30 24 Le temps est relatif : comme une coordonnée, il dépend du référentiel. La durée du voyage de A, égal à 2T0 est multiplié pour B par le facteur
Pour bien percevoir l'effet relativiste, il faut voir ce que donnerait le formalisme classique. Il suffit de supposer qu'au lieu de s'envoyer des messages électro-magnétiques, A et B s'envoie des messages sonores à intervalle régulier. Nous supposerons que le milieu dans lequel se déplacent ces ondes sonores coïncide avec le référentiel de B. Le facteur de l' effet Doppler demeure, mais au sens classique.
- En ce qui concerne les messages émis de B vers A, A les perçoit à l'aller en ralenti avec le facteur (1 − v / c), et au retour en accéléré avec le facteur (1 + v / c), sans le facteur spécifiquement relativiste de dilatation du temps
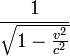 . La longueur du trajet de A est 3cT0/5, soit 3/5 a.l. (nous gardons les mêmes unités même si elles ne sont plus vraisemblables pour faciliter la comparaison).
. La longueur du trajet de A est 3cT0/5, soit 3/5 a.l. (nous gardons les mêmes unités même si elles ne sont plus vraisemblables pour faciliter la comparaison).
- En ce qui concerne les messages émis de A vers B, B les perçoit à l'aller de A en ralenti avec le facteur
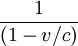 , et au retour de A en accéléré avec le facteur
, et au retour de A en accéléré avec le facteur 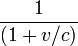 .
.
-
- Point de vue de A : Pendant le voyage aller d'un an (sic), A reçoit au ralenti la vie de B avec un facteur 1 - 3/5, soit 2/5 de la vie de B. Au retour, A reçoit en accéléré la vie de B avec un facteur 1 + 3/5, soit 8/5 de la vie de B. Au cours de ses deux ans de voyage, A a visionné 2/5 + 8/5 = 2 années de la vie de B.
- Point de vue de B : B reçoit au ralenti une année de voyage de A, avec un facteur 1/(1 + 3/5)) = 5/8. À cet instant, A fait demi-tour, mais B ne le sait pas encore. Il le saura lorsque le signal émis par A lui parviendra, c’est-à-dire dans 3/5 d'année. B verra donc s'écouler 1 + 3/5 = 8/5 d'années pour visionner la totalité du voyage de A avant de le voir faire demi-tour. Ces 8/5 d'années correspondent bien à un an de la vie de A visionnée au ralenti avec un facteur 5/8. Lorsque B voit A faire demi-tour, A est déjà sur le chemin du retour depuis 3/5 d'année. Il lui reste donc 2/5 d'année à voyager. B, quant à lui, visionnera en accéléré la totalité du voyage retour avec un facteur 1/(1 - 3/5)) = 5/2. Ce visionnage du retour durera donc également 2/5 d'année, et B aura visionné 8/5 + 2/5 = 2 années de voyage de A.
L'aller et le retour de A ont duré chacun 1 an, A a vécu 2 ans. Et B a vécu 2 ans pour visionner les 2 ans du voyage de A : classique quoi ! Le temps est le même pour A et B : universel.
Forces et Accélérations
Le quadrivecteur accélération
De même que nous avons défini le quadrivecteur vitesse en différentiant le quadrivecteur position par rapport au temps propre, nous pouvons définir le quadri-accélération en différentiant le quadrivecteur vitesse par rapport au temps propre :
avec
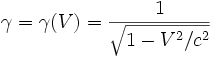
La transformation des accélérations
La transformation de Lorentz appliquée sur le quadrivecteur accélération dans un référentiel
 permet d'en déduire le quadrivecteur accélération dans le référentiel
permet d'en déduire le quadrivecteur accélération dans le référentiel  , et de calculer explicitement les composantes de l'accélération. Notons
, et de calculer explicitement les composantes de l'accélération. Notons 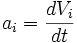 la ième composante dans le référentiel
la ième composante dans le référentiel  et notons-la
et notons-la 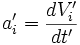 dans le repère
dans le repère  . On obtient, en notant v la vitesse de
. On obtient, en notant v la vitesse de  par rapport à
par rapport à  :
:Lorsque vx = v et vy = vz = 0 (vitesse et accélération parallèles), on a
Cette relation est importante car elle peut servir à obtenir la variation de la masse avec la vitesse et, donc, E = mc2 [1].
Lorsque vy = v et vx = vz = 0 (vitesse et accélération perpendiculaires), on a
Cette formule est utile pour un mouvement de rotation et sert pour l'obtention de la formule de Larmor relativiste.
Le mouvement uniformément accéléré
Considérons un référentiel inertiel
 . Supposons que M, particule de masse m0, se déplace sous l'effet d'une force constante F parallèle à Ox et que, pour t = 0, M soit en O avec une vitesse nulle. Sous l'effet de la force, la particule va être soumise à une accélération. Cependant, celle-ci ne saurait être constante, égale à
. Supposons que M, particule de masse m0, se déplace sous l'effet d'une force constante F parallèle à Ox et que, pour t = 0, M soit en O avec une vitesse nulle. Sous l'effet de la force, la particule va être soumise à une accélération. Cependant, celle-ci ne saurait être constante, égale à 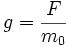 , sous peine de voir la particule atteindre puis dépasser la vitesse de la lumière. Quel est alors l'équivalent relativiste du mouvement uniformément accéléré de la mécanique galiléenne ?
, sous peine de voir la particule atteindre puis dépasser la vitesse de la lumière. Quel est alors l'équivalent relativiste du mouvement uniformément accéléré de la mécanique galiléenne ?À un instant t donné, le point M est animé d'une vitesse V par rapport à
 . Considérons alors un référentiel
. Considérons alors un référentiel  se déplaçant à la vitesse constante v qui coïncide à l'instant t avec la vitesse V de M, et tel que son origine O' coïncide également avec M à l'instant t. Dans ce référentiel
se déplaçant à la vitesse constante v qui coïncide à l'instant t avec la vitesse V de M, et tel que son origine O' coïncide également avec M à l'instant t. Dans ce référentiel  , au cours du temps, le point M se voit se rapprocher de O', atteindre ce point en un certain instant t', sa vitesse V' s'annule en cet instant, puis il repart et s'éloigne de O'. Il est alors soumis à une accélération a'x dans le repère
, au cours du temps, le point M se voit se rapprocher de O', atteindre ce point en un certain instant t', sa vitesse V' s'annule en cet instant, puis il repart et s'éloigne de O'. Il est alors soumis à une accélération a'x dans le repère  . Puisque la vitesse V' s'annule au moment où M atteint O', nous ferons l'hypothèse que les lois de la mécanique galiléenne s'applique à cet instant, et que l'accélération a'x est égale à g. Selon les règles de transformation des accélérations vues précédemment, et compte tenu du fait que v = V = Vx, l'accélération de la particule M dans le référentiel
. Puisque la vitesse V' s'annule au moment où M atteint O', nous ferons l'hypothèse que les lois de la mécanique galiléenne s'applique à cet instant, et que l'accélération a'x est égale à g. Selon les règles de transformation des accélérations vues précédemment, et compte tenu du fait que v = V = Vx, l'accélération de la particule M dans le référentiel  à l'instant t est
à l'instant t est 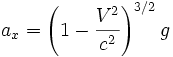 .
.Si, à chaque instant t, on redéfinit le référentiel
 coïncidant avec M, alors on définit ainsi une accélération propre constante a'x = g et une accélération dans le référentiel
coïncidant avec M, alors on définit ainsi une accélération propre constante a'x = g et une accélération dans le référentiel  égale à :
égale à :Au fur et à mesure que V augmente et se rapproche de c, l'accélération de la particule dans le référentiel
 diminue, bien que son accélération dans son référentiel propre reste constante. L'intégration de l'équation donne l'expression de V en fonction du temps, à savoir :
diminue, bien que son accélération dans son référentiel propre reste constante. L'intégration de l'équation donne l'expression de V en fonction du temps, à savoir :On constate que V tend vers c lorsque t tend vers l'infini. Par ailleurs, pour t proche de 0, on retrouve l'expression V = gt de la mécanique galiléenne. Une deuxième intégration fournit l'expression de l'abscisse x du point mobile M :
Pour t proche de 0, on retrouve l'expression
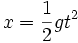 de la mécanique galiléenne.
de la mécanique galiléenne.Accélération et énergie
Si, dans l'étude du paragraphe précédent, on souhaite que la loi
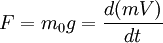 reste valide, il faut, puisque dV/dt n'est pas constant, que m ne le soit pas non plus. F étant constante, on a nécessairement mV = Ft avec, comme on l'a vu :
reste valide, il faut, puisque dV/dt n'est pas constant, que m ne le soit pas non plus. F étant constante, on a nécessairement mV = Ft avec, comme on l'a vu :ce qui donne :
On obtient alors :
Ainsi, lorsque V augmente, on est amené à attribuer une masse m en mouvement de plus en plus importante, afin que la loi fondamentale de la dynamique reste valide.
E = mc2
Toujours dans le cadre de l'étude précédente, la particule M voit son énergie varier avec la puissance suivante :
or :
-
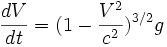 et
et 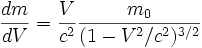
d'où, après simplification :
ce qui conduit à la formule la plus célèbre de la physique :
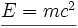
On remarque que la variation d'énergie depuis l'instant initial est :
qui donne
 pour les petites vitesses. On retrouve l'expression classique de l'énergie cinétique.
pour les petites vitesses. On retrouve l'expression classique de l'énergie cinétique.Le quadrivecteur force et la transformation des forces
Soit une particule de masse m0, se déplaçant à la vitesse
 par rapport à un référentiel inertiel
par rapport à un référentiel inertiel  . On peut, comme en mécanique classique, définir la force à laquelle est soumise cette particule si sa quantité de mouvement varie, par :
. On peut, comme en mécanique classique, définir la force à laquelle est soumise cette particule si sa quantité de mouvement varie, par :avec
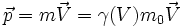 , et sa variation d'énergie par :
, et sa variation d'énergie par :Mais pour passer d'un référentiel à l'autre, il vaut mieux utiliser le quadrivecteur force défini comme la dérivée du quadrivecteur impulsion par rapport au temps propre :
L'application d'une transformation de Lorentz à ce quadrivecteur permet de savoir comment une force se transforme d'un référentiel à l'autre.
Si (Fx,Fy,Fz) sont les composantes de
 dans le référentiel
dans le référentiel  et si (F'x,F'y,F'z) sont ses composantes dans le référentiel
et si (F'x,F'y,F'z) sont ses composantes dans le référentiel  en translation de vitesse v par rapport à
en translation de vitesse v par rapport à  , alors on trouve que :
, alors on trouve que :avec
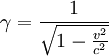 et
et 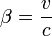 .
.En particulier, si la vitesse V du point mobile coïncide à un instant donné avec la vitesse v du référentiel
 , alors F'x = Fx, par contre les deux autres composantes sont différentes.
, alors F'x = Fx, par contre les deux autres composantes sont différentes.Exemple 1 : chute libre
Considérons une particule de masse m0 située en t = 0 en O et se déplaçant à la vitesse v selon l'axe Ox. On lui applique une force constante F = m0g selon l'axe Oy. En mécanique galiléenne, sa trajectoire est une parabole. Qu'en est-il en mécanique relativiste ?
En écrivant que
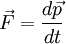 et en projetant cette relation sur deux axes, on obtient, en notant Vx et Vy les composantes de sa vitesse V à l'instant t :
et en projetant cette relation sur deux axes, on obtient, en notant Vx et Vy les composantes de sa vitesse V à l'instant t :d'où :
La résolution de ce système conduit à :
et l'intégration de ces deux relations donnent les coordonnées x et y de la particule à l'instant t :
où sinh-1 est la réciproque du sinus hyperbolique. Si on exprime y en fonction de x, on obtient :
qui est l'équation d'une chaînette et non plus d'une parabole.
On peut retrouver les solutions de la mécanique galiléenne en augmentant indéfiniment la valeur de c, ce qui donne :
Exemple 2 : champ électrique
On considère dans le référentiel
 un champ électrique
un champ électrique  , et une particule de charge q, se déplaçant dans ce champ. Celle-ci est soumise à une force
, et une particule de charge q, se déplaçant dans ce champ. Celle-ci est soumise à une force  . Qu'en est-il dans le référentiel
. Qu'en est-il dans le référentiel  en déplacement à la vitesse v parallèle à Ox par rapport à
en déplacement à la vitesse v parallèle à Ox par rapport à  ?
?À partir des relations :
avec
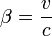 et
et 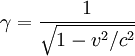 , on en déduit que :
, on en déduit que :La force
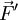 est de la forme :
est de la forme :avec
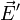 champ électrique de composantes
champ électrique de composantes 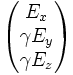 et
et  champ magnétique de composantes
champ magnétique de composantes 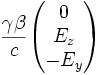
Ainsi, le fait de changer de référentiel a légèrement modifié les composantes du champ électrique orthogonales au déplacement, et a fait apparaître un champ magnétique. Ce champ n'est que l'effet relativiste du changement de référentiel.
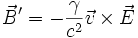
Exemple 3 : champ magnétique
On considère maintenant la même particule, mais dans un champ magnétique
 . La force à laquelle la particule est soumise est cette fois :
. La force à laquelle la particule est soumise est cette fois :Les composantes de cette force sont :
En opérant comme dans le paragraphe précédent, on trouve les composantes de la force dans le référentiel
 :
:La force
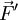 est de la forme :
est de la forme :avec ici
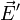 champ électrique de composantes
champ électrique de composantes 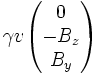 et
et  champ magnétique de composantes
champ magnétique de composantes 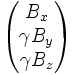 .
.Ainsi, le fait de changer de référentiel a légèrement modifié les composantes du champ magnétique orthogonales au déplacement, et a fait apparaître un champ électrique. Ce champ est aussi un effet relativiste du changement de référentiel.
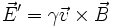
Si on combine les exemples 2 et 3, on obtient les transformations d'un champ électro-magnétique
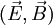 :
:ou encore, en désignant par
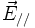 et
et 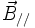 les composantes des champs parallèles au sens du déplacement du référentiel
les composantes des champs parallèles au sens du déplacement du référentiel  , et par
, et par 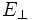 et
et  les composantes orthogonales :
les composantes orthogonales :Tout ceci fait intervenir deux champs
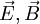 classiques qui lors d'un changement de référentiel se 'transforment' l'un dans l'autre sans pour cela se mettre clairement sous la forme de quadrivecteur comme l'énergie impulsion etc. Par contre les équations de Maxwell prennent une forme relativiste et
classiques qui lors d'un changement de référentiel se 'transforment' l'un dans l'autre sans pour cela se mettre clairement sous la forme de quadrivecteur comme l'énergie impulsion etc. Par contre les équations de Maxwell prennent une forme relativiste et 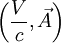 va se transformer comme doit le faire un quadrivecteur ce qui fait dire à Feynman que si dans les champs électromagnétique il fallait mettre une hiérarchie c'est de considérer d'abord les grandeurs quadrivecteurs. Il faut donc essayer de formuler les équations de Maxwell avec des opérateurs et des champs vectoriels ou tensoriel à 4 dimensions.
va se transformer comme doit le faire un quadrivecteur ce qui fait dire à Feynman que si dans les champs électromagnétique il fallait mettre une hiérarchie c'est de considérer d'abord les grandeurs quadrivecteurs. Il faut donc essayer de formuler les équations de Maxwell avec des opérateurs et des champs vectoriels ou tensoriel à 4 dimensions.Optique relativiste
On utilise en optique relativiste les quadrivecteurs de la forme
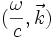 , où ω est la pulsation de l'onde, et
, où ω est la pulsation de l'onde, et 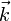 le vecteur d'onde indiquant la direction de propagation de l'onde et de module ω/c. Ce quadrivecteur est l'équivalent pour une onde électromagnétique du quadrivecteur
le vecteur d'onde indiquant la direction de propagation de l'onde et de module ω/c. Ce quadrivecteur est l'équivalent pour une onde électromagnétique du quadrivecteur 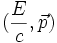 énergie-impulsion pour une particule, multiplié par la constante de Planck
énergie-impulsion pour une particule, multiplié par la constante de Planck  . En effet, la dualité onde-particule attribue à une onde une énergie
. En effet, la dualité onde-particule attribue à une onde une énergie 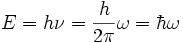 , et une quantité de mouvement dont le module est
, et une quantité de mouvement dont le module est 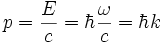 .
.La transformation d'un référentiel à l'autre de ce quadrivecteur explique les deux effets suivants :
Le quadrivecteur énergie impulsion
Pour exprimer le quadrivecteur énergie impulsion d'une particule de masse m0 se déplaçant à la vitesse
 , il suffit de considérer une masse m0 et de former comme en mécanique classique l'impulsion qui est le produit de la masse par la vitesse.
, il suffit de considérer une masse m0 et de former comme en mécanique classique l'impulsion qui est le produit de la masse par la vitesse.En mécanique relativiste, nous formons le produit de la masse par la quadri-vitesse, obtenant ainsi le quadrivecteur énergie-impulsion :
Dans la définition du quadrivecteur, on a posé :
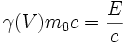 où E est l'énergie associée à la particule en mouvement. E = γ(V)m0c2
où E est l'énergie associée à la particule en mouvement. E = γ(V)m0c2-
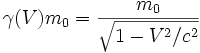 , quantité qui tend vers l'infini quand V tend vers c a souvent été utilisée au XXième siècle en termes de masse variable.
, quantité qui tend vers l'infini quand V tend vers c a souvent été utilisée au XXième siècle en termes de masse variable.
On préfère aujourd'hui réserver le mot masse pour désigner l'énergie propre d'une particule ; c’est-à-dire son énergie au repos.
Les chocs aux hautes énergies
La principale confirmation de la relativité est aujourd'hui facilement illustrée par ce qu'on appelle la physique des particules ou encore des hautes énergies. Les accélérateurs de particules frappent par la dimension des installations ; ce sont des tubes (dans lequel on fait le vide) de plusieurs kilomètres en forme d'anneau creux ou tore dans lequel sont injectés des 'paquets' de protons qui circulent à grandes vitesses après avoir été accélérés par des champs électriques et déviés par des champs magnétiques qui leur imposent de rester à tourner dans le tube. Ainsi il est possible de faire des chocs de protons contre des protons à hautes énergies.
Référentiels particuliers
On considère en général deux référentiels : le référentiel où la cible 2 est au repos dit du laboratoire SL
et le référentiel où le tout est immobile dit à tort du centre de masse SCM
Exemple de choc
si on a une particule de masse m1 qui vient percuter une particule de masse m2, on écrira en relativité restreinte la conservation du quadrivecteur impulsion :
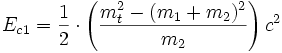 et
et 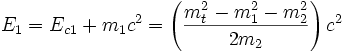
 On peut donc en déduire le γ permettant de passer du système du laboratoire (cible 2 immobile) au système dit du centre de masse (l'ensemble est immobile)
On peut donc en déduire le γ permettant de passer du système du laboratoire (cible 2 immobile) au système dit du centre de masse (l'ensemble est immobile)
 et le :
et le :
- La pseudonorme du tout donne la masse totale exprimée dans SL en fonction de m1,m2 et Ec1.
Le défaut de masse
Dans l'exemple précédent, mt était supérieure à la somme des masses m1 et m2. À l'inverse, lors d'une désintégration radioactive, la masse des particules formées est inférieure à la masse initiale. La réaction a produit de l'énergie : elle est exoénergétique. Ce qui donne aussitôt dans le référentiel dit du centre de masse celui où la particule mt est immobile :
-
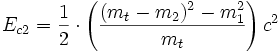 et
et 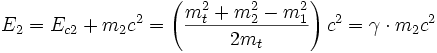
 et le :
et le :
-
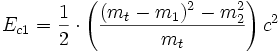 et
et 

Les lois de l'électromagnétisme
L'équation de conservation de la charge électrique s'écrit :
 La force de Lorentz s'écrit :
La force de Lorentz s'écrit :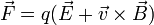
Les équations de Maxwell s'écrivent sous forme vectorielle
Écrites dans le formalisme de Lorentz avec des quadrivecteurs, elles se simplifient.
On pose comme quadri-vecteur courant
 . En effet, soit ρ0 la densité de charge dans le référentiel propre, se déplaçant à la vitesse
. En effet, soit ρ0 la densité de charge dans le référentiel propre, se déplaçant à la vitesse  par rapport à un référentiel
par rapport à un référentiel  . Du fait de la contraction des longueurs dans la direction de
. Du fait de la contraction des longueurs dans la direction de  , le volume occupé par une charge donnée sera multiplié par le facteur
, le volume occupé par une charge donnée sera multiplié par le facteur 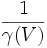 lorsqu'il est observé depuis le référentiel
lorsqu'il est observé depuis le référentiel  , et donc la densité de charge dans ce même référentiel sera γ(V)ρ0. Par ailleurs, la densité de courant est
, et donc la densité de charge dans ce même référentiel sera γ(V)ρ0. Par ailleurs, la densité de courant est 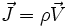 , de sorte que :
, de sorte que :-
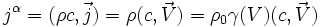 produit de ρ0 par le quadrivecteur vitesse.
produit de ρ0 par le quadrivecteur vitesse.
On peut alors appliquer les transformations de Lorentz pour déterminer comment sont transformées densité de charge et densité de courant d'un référentiel
 à un référentiel
à un référentiel  .
.Nous avons donc comme formule de transformation des courants et des densités de courant (pour un référentiel en translation uniforme) :
De la même façon, on a comme transformation pour les potentiels :
On définit le quadri-potentiel électromagnétique :
- Nous définissons le champ électromagnétique de la façon suivante :
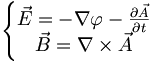
Les transformations des composantes du champ électromagnétique s'écrivent :
- On peut alors définir :
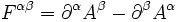
- Le Tenseur électromagnétique F est anti-symétrique, nous pouvons calculer ses composantes :
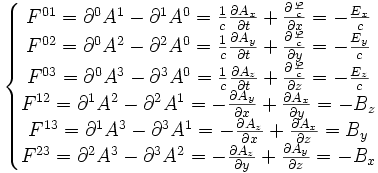
- Le tenseur électromagnétique s'écrit sous forme matricielle :
![F^{\alpha\beta}=\left[\begin{matrix}
0 & -\frac{E_x}{c} & -\frac{E_y}{c} & -\frac{E_z}{c}\\
\frac{E_x}{c} & 0 & -B_z & B_y\\
\frac{E_y}{c} & B_z & 0 & -B_x\\
\frac{E_z}{c} & -B_y & B_x & 0
\end{matrix}\right]](/pictures/frwiki/48/00434fce2fb99b81ce2b089ed0b74a8c.png)
Les équations contenant les sources (1) et (4) s'écrivent dans la formulation covariante :
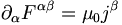
- En effet, on a :
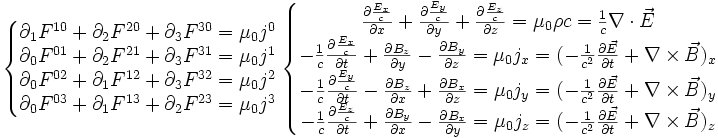
Les équations (2) et (3) s'écrivent :
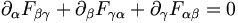
- La vérification est aisée.
L'équation s'écrit aussi avec le tenseur de Lévi-Civita :
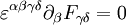
Autres ébauches
- les intervalles d'espace
- etc.
Références
Voir aussi
- Portail de la physique
Catégorie : Relativité -
Wikimedia Foundation. 2010.


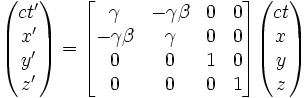
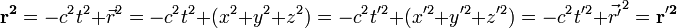
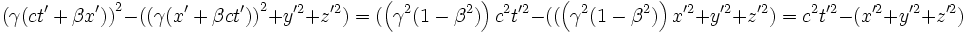
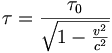
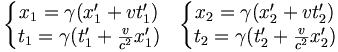
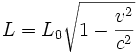
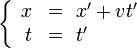
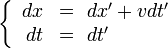
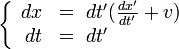

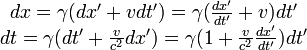

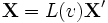
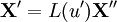


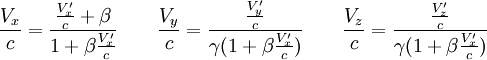
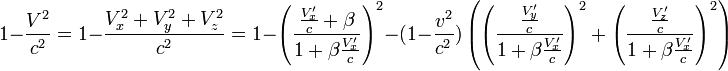



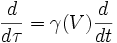
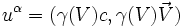
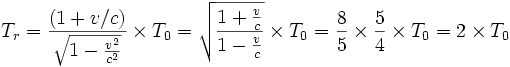

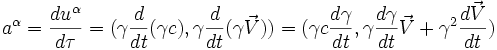
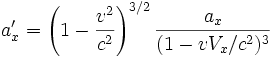

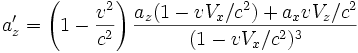
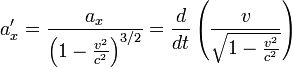

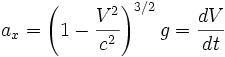
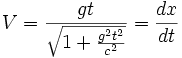
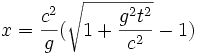
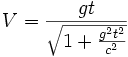

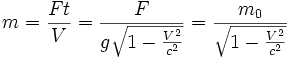
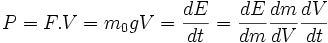
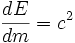
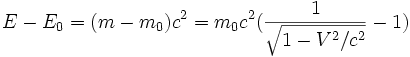
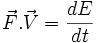
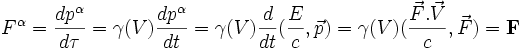
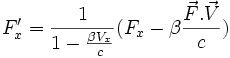
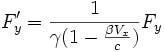
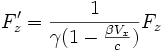
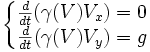
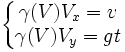
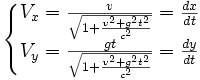
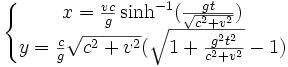
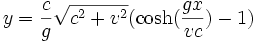

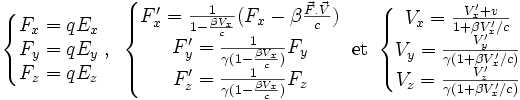
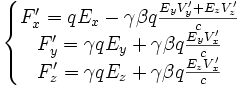
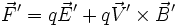
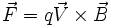
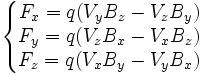


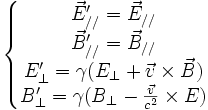

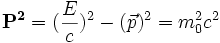
![\mathbf{P}=\begin{pmatrix}
\\ \frac {E}{c}\\
\ p_x\\
\ p_y\\
\ p_z\\\end{pmatrix} = \begin{bmatrix}
\gamma & \gamma\beta& 0 & 0\\
\gamma\beta & \gamma & 0& 0\\
0 & 0 & 1& 0\\
0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix}
\\ \frac {E'}{c}\\
\ p'_x\\
\ p'_y\\
\ p'_z\\\end{pmatrix}= \mathbf{[\mathcal{L}]}*\mathbf{P'}](/pictures/frwiki/100/da41eb5983c9ee1cf330c2a3f0b91b2a.png)