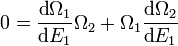Bêta thermodynamique

Bêta thermodynamique

Température inverse

La température inverse, notée β et parfois dite bêta thermodynamique, est une grandeur physique utilisée en physique statistique. Elle reliée à la température T d'un système par β = 1/(kT), où k est la constante de Boltzmann.[1],[2] Son unité est le J-1.

Sommaire

Interprétation

Physique statistique

On considère un système composé deux sous-systèmes, d'énergies E1 et E2. Le nombre de micro-états du système peut s'écrire en fonction de ceux des sous-systèmes :

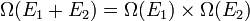\Omega(E_1+E_2) = \Omega(E_1) \times \Omega(E_2).

Cette relation est caractéristique de la fonction exponentielle et pousse à poser

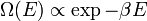\Omega(E) \propto \exp -\beta E,

où β est à relier à la température du système lorsqu'il est à l'équilibre thermodynamique.[3] Une autre version de l'interprétation utilise le fait que Ω est maximum à l'équilibre thermodynamique, ainsi que la relation E = E1+E2 pour un système isolé. Dès lors,

0 = \frac{\text{d}\Omega_1}{\text{d}E_1} \Omega_2 + \Omega_1\frac{\text{d}\Omega_2}{\text{d}E_1}

ce qui, avec dE1 = −dE2, donne

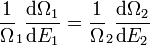\frac 1\Omega_1 \frac{\text{d}\Omega_1}{\text{d}E_1} = \frac 1\Omega_2 \frac{\text{d}\Omega_2}{\text{d}E_2}.

Cela motive l'écriture d'un paramètre

\beta = \frac{\text{d}\log \Omega}{\text{d}E}

qui est relié à la température, car à l'équilibre β1 = β2.[réf. nécessaire]

Formulaire

Principales relations entre la température inverse et les variables d'un système.
Contexte Formule Notations
Thermodynamique
Théorie cinétique des gaz
Physique statistique[1]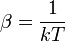		 \beta = \frac 1{kT}
Ensemble microcanonique[1] 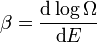\beta = \frac{\text{d} \log \Omega}{\text{d}E}
Ensemble canonique[4] 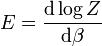E = \frac{\text{d}\log Z}{\text{d}\beta}
Thermodynamique[5] 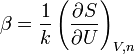\beta = \frac 1k \left(\frac{\partial S}{\partial U}\right)_{V,n}

Sources

Bibliographie

  • Dietrich Stauffer, H. E. Stanley, Annick Lesne, Cours de Physique : De Newton à Mandelbrot, Springer, 1999 (ISBN 2287596747) 

Références

  1. ↑ a , b  et c  (en) Eric W. Weisstein (dir.), « Thermodynamic Beta » sur Science World
  2. ↑ (fr) Stauffer et al. (1999), p. 164
  3. ↑ (fr) Stauffer et al. (1999), p. 166 (l'argument original utilise la densité de probabilité)
  4. ↑ (en) Michael Plischke, Birger Bergersen, Equilibrium Statistical Physics, World Scientific, 2005 (ISBN 9812560483), p. 39 
  5. ↑ (fr) Stauffer et al. (1999), p. 173 (la formule originale utilise 1/T)

Annexes

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « Temp%C3%A9rature inverse ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Bêta thermodynamique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Beta thermodynamique — Température inverse La température inverse, notée β et parfois dite bêta thermodynamique, est une grandeur physique utilisée en physique statistique. Elle reliée à la température T d un système par β = 1/(kT), où k est la constante de… …   Wikipédia en Français

  • Béta — Bêta  Pour l’article homophone, voir Beta. Pour les articles homonymes, voir Bêta (homonymie). Bêta …   Wikipédia en Français

  • Bêta (homonymie) —  Pour l’article homophone, voir Beta (homonymie). Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Bêta est la deuxième lettre de l alphabet grec ; Le test bêta est la deuxième période d essai… …   Wikipédia en Français

  • Thermodynamique statistique — Physique statistique La physique statistique a pour but d expliquer le comportement et l évolution de systèmes physiques comportant un grand nombre de particules (on parle de systèmes macroscopiques), à partir des caractéristiques de leurs… …   Wikipédia en Français

  • Formules De Thermodynamique — En thermodynamique moderne, les fonctions d état caractéristiques corps pur peuvent être exprimées au moyen de nombreuses relations. Les fonctions d état sont : la pression p, la température T, le volume V, l énergie interne U, l entropie S …   Wikipédia en Français

  • Formules de thermodynamique — En thermodynamique moderne, les fonctions d état caractéristiques d un corps pur peuvent être exprimées au moyen de nombreuses relations. Les fonctions d état sont : la pression p, la température T, le volume V, l énergie interne U, l… …   Wikipédia en Français

  • Β — Bêta  Pour l’article homophone, voir Beta. Pour les articles homonymes, voir Bêta (homonymie). Bêta …   Wikipédia en Français

  • Température inverse — La température inverse, notée β et parfois dite bêta thermodynamique, est une grandeur physique utilisée en physique statistique. Elle reliée à la température T d un système par β = 1/(kT), où k est la constante de Boltzmann[1],[2]. Son unité est …   Wikipédia en Français

  • Distribution De Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… …   Wikipédia en Français

  • Distribution de Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”