- Premier snark de Blanuša
-
Premier snark de Blanuša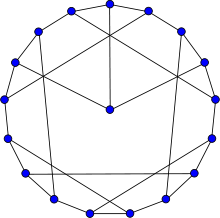 
Représentation du premier snark de BlanušaNombre de sommets 18 Nombre d'arêtes 27 Distribution des degrés 3-régulier Rayon 4 Diamètre 4 Maille 5 Automorphismes 8 (D4) Nombre chromatique 3 Indice chromatique 4 Propriétés Régulier
Snark
Cubique
Hypohamiltonienmodifier 
Le premier snark de Blanuša est, en théorie des graphes, un graphe 3-régulier possédant 18 sommets et 27 arêtes.
Sommaire
Propriétés
Propriétés générales
Le diamètre du premier snark de Blanuša, l'excentricité maximale de ses sommets, est 4, son rayon, l'excentricité minimale de ses sommets, est 4 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloriage
Le nombre chromatique du premier snark de Blanuša est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du premier snark de Blanuša est 4. Il existe donc une 4-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal. Le premier snark de Blanuša est donc un snark, un graphe connexe, sans pont, cubique, de maille au moins 5 et d'indice chromatique 4. De 1898 à 1946, le graphe de Petersen est le seul snark connu, jusqu'à ce que la Danilo Blanuša exhibe deux autres exemples, le premier snark de Blanuša et le second snark de Blanuša[1].
Le théorème du snark, un résultat conjecturé par W. T. Tutte et prouvé en 2001 par Robertson, Sanders, Seymour et Thomas, affirme que tout snark admet le graphe de Petersen comme mineur[2]. Le premier snark de Blanuša admet donc le graphe de Petersen comme mineur.
Propriétés algébriques
Le groupe d'automorphismes du premier snark de Blanuša est un groupe d'ordre 8 isomorphe au groupe diédral D4, le groupe des isométries du plan conservant un carré. Ce groupe est constitué de 4 éléments correspondant aux rotations et de 4 autres correspondant aux réflexions.
Le polynôme caractéristique du premier snark de Blanuša est : (x − 3)(x − 1)3(x + 1)(x + 2)(x4 + x3 − 7x2 − 5x + 6)(x4 + x3 − 5x2 − 3x + 4)2.
Snarks de Blanuša généralisés
Il existe une généralisation du premier et du second snark de Blanuša en deux familles infinies de snarks d'ordre 8n+10. Elles sont notées respectivement
et 
. Les snarks de Blanuša sont les deux plus petits membres de ces familles infinies[3].Voir aussi
Liens internes
- Théorie des graphes
- Snark (théorie des graphes)
- Second snark de Blanuša
Liens externes
- (en) Eric W. Weisstein, Blanuša Snarks (MathWorld)
Références
- Danilo Blanuša, « Problem četiriju boja », dans Glasnik Mat. Fiz. Astr. Ser II, vol. 1, 1946, p. 31–42
- (en) Ed, Jr. Pegg, Book Review: The Colossal Book of Mathematics, vol. 49, 2002 [lire en ligne], p. 1084–1086.
- (en) Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.
Catégorie :- Graphe remarquable
Wikimedia Foundation. 2010.
