Arc cosinus

Arc cosinus
Représentation graphique

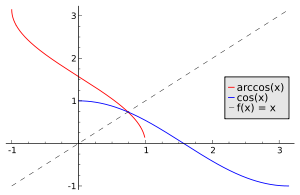
En mathématiques, l’arc cosinus d'un nombre réel compris entre −1 et 1 est l'unique mesure d'angle dont le cosinus vaut ce nombre, entre l'angle nul et l'angle plat.

La fonction qui associe à tout nombre réel entre −1 et 1 la valeur de son arc cosinus en radians est en général notée[1] Arc cos en notation française (bien que la norme ISO 31-11 recommande la notation arccos), et cos−1, parfois acos ou acs, en notation anglo-saxonne. Il s'agit alors de la réciproque de la fonction trigonométrique cosinus sur l'intervalle [0 ; π].

Sommaire

Dérivée

Comme dérivée d'une fonction réciproque, Arccos est dérivable sur ]-1,1[ et vérifie

\mathrm{Arccos}' x = \frac{-1}{\sqrt{1-x^2}}

Cette formule s'obtient grâce au théorème sur la dérivée d'une fonction réciproque.

Forme intégrale indéfinie

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie :

\mathrm{Arccos}(x) = \int_1^x-\frac{1}{\sqrt{1 - t^{2}}}dt

Primitives

Les primitives de l'arc cosinus s'obtiennent par intégration par parties

\int \mathrm{Arccos}(x) \,dx = x\, \mathrm{Arccos}(x) - \sqrt{1-x^2} + C

Relation entre Arc cosinus et Arc sinus

\mathrm{Arccos}(x) + \mathrm{Arcsin}(x) = \frac{\pi}{2}

Preuve par la dérivée

Soit f la fonction qui à x dans [-1,1] associe Arccos(x) + Arcsin(x). Sa dérivée est nulle :

\forall x \in [-1,1], f'(x) = \mathrm{Arccos}'(x) + \mathrm{Arcsin}'(x) = \frac{-1}{\sqrt{1-x^2}} + \frac{1}{\sqrt{1-x^2}} = 0

Donc f est constante sur son ensemble de définition. Donc :

\forall x \in [-1,1], f(x)=f(0)=\mathrm{Arccos}(0) + \mathrm{Arcsin}(0)=\frac{\pi}{2}+0=\frac{\pi}{2}

Preuve trigonométrique

Pour tout x dans [-1,1], on pose \alpha = \frac{\pi}{2} - \mathrm{Arccos}(x).

On calcule \sin(\alpha) = \sin(\frac{\pi}{2} - \mathrm{Arccos}(x)) = cos( \mathrm{Arccos}(x)) = x.

Or \mathrm{Arccos}(x) \in [0,\pi] donc \alpha \in \left[-\frac{\pi}{2} ; \frac{\pi}{2} \right].

Donc α = Arcsin(x).

Donc \mathrm{Arccos}(x) + \mathrm{Arcsin}(x) = \frac{\pi}{2} - \alpha + \alpha = \frac{\pi}{2}

 
Arccos(x) (bleu) et Arcsin(x) (rouge).

Forme logarithmique

On peut exprimer la fonction arc cosinus avec un logarithme complexe :

\mathrm{Arccos}(x) = -i\,\ln\left(x+i\,\sqrt{1-x^2}\right) = \frac{\pi}{2}\,+i\ln\left(i\,x+\sqrt{1-x^2}\right) = \frac{\pi}{2}-\mathrm{Arcsin}(x)

Voir aussi

Notes et références

  1. ↑ « Exponentielle & logarithme », § Fonctions circulaires réciproques, Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Arc cosinus de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • ARC — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. {{{image}}}   Sigles d une seule lettre   Sigles de deux lettres > Sigles de trois lettres …   Wikipédia en Français

  • arc — 1. arc [ ark ] n. m. • 1080; lat. arcus 1 ♦ Arme formée d une tige souple (de bois, de métal) que l on courbe au moyen d une corde attachée aux deux extrémités pour lancer des flèches. Arc et arbalète. Bander, tendre l arc. Tirer des flèches avec …   Encyclopédie Universelle

  • Arc — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.   Sigles d’une seule lettre   Sigles de deux lettres > Sigles de trois lettres   Sigles de quatre lettres …   Wikipédia en Français

  • Arc sinus — Pour les articles homonymes, voir ASIN. Représentation graphique En mathématiques, l’arc sinus d un nombre réel compris entre −1 et 1 est l unique mesure d angle …   Wikipédia en Français

  • Arc tangente — Représentation graphique En mathématiques, l’arc tangente d un nombre réel est la mesure d un angle orienté dont la tangente vaut ce nombre. La fonction qui à tout nombre réel associe la valeur de son arc tangente en radians est la réciproque de… …   Wikipédia en Français

  • Cosinus — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u …   Wikipédia en Français

  • Cosinus hyperbolique — Graphe de la fonction cosinus hyperbolique sur une partie de Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique. Sommaire …   Wikipédia en Français

  • Arc caténaire — Chaînette Courbe de la chaînette pour a=2 En mathématiques, la chaînette est une courbe plane transcendante, qui correspond à la forme que prend un câble (ou une chaîne) lorsqu il est suspendu par ses extrémités et soumis à une force… …   Wikipédia en Français

  • Arc rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une …   Wikipédia en Français

  • ARC — s. m. Sorte d arme servant à lancer des flèches : elle est formée d une branche de bois ou d une verge, soit de métal, soit d autre matière, courbée avec effort au moyen d une corde qui s attache aux deux extrémités. Arc de corne. La poignée d un …   Dictionnaire de l'Academie Francaise, 7eme edition (1835)

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”