Arc sinus

Arc sinus
Page d'aide sur l'homonymie Pour les articles homonymes, voir ASIN.
Représentation graphique

En mathématiques, l’arc sinus d'un nombre réel compris entre −1 et 1 est l'unique mesure d'angle dont le sinus vaut ce nombre, entre −π/2 et π/2.

La fonction qui associe à tout nombre réel entre −1 et 1 la valeur de son arc sinus en radians est en général notée[1] Arc sin en notation française (bien que la norme ISO 31-11 recommande la notation arcsin), et sin−1, parfois asin ou asn, en notation anglo-saxonne. Il s'agit alors de la réciproque de la fonction sinus sur l'intervalle [-π/2 ; π/2].

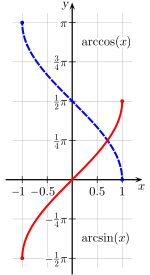
La courbe représentative de la fonction arc sinus est obtenue à partir de la courbe représentative de la restriction de la fonction sinus à l'intervalle [-π/2 ; π/2] par une réflexion d'axe la droite d'équation y = x.

Sommaire

Dérivée

Comme dérivée d'une fonction réciproque, Arcsin est dérivable sur ]-1:1[ et vérifie

\mathrm{Arcsin}'(x) = \frac{1}{\sqrt{1-x^2}}

Cette formule s'obtient grâce au théorème sur la dérivée d'une fonction réciproque.

Forme intégrale indéfinie

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie :

\mathrm{Arcsin}(x) = \int_0^x\frac{1}{\sqrt{1 - t^{2}}}dt

Primitives

Les primitives de l'arc sinus s'obtiennent par intégration par parties

\int \mathrm{Arcsin}(x) \,dx = x\, \mathrm{Arcsin}(x) + \sqrt{1-x^2} + C

Relation importante

Arccos(x) (bleu) et Arcsin(x) (rouge).

La relation suivante entre l'arc cosinus et l'arc sinus se démontre en utilisant le fait que la dérivée est nulle et en calculant la valeur en un point. \mathrm{Arccos}(x) + \mathrm{Arcsin}(x) = \frac{\pi}{2}

Forme logarithmique

On peut exprimer la fonction arc sinus avec un logarithme complexe :

\mathrm{Arcsin}(x) = -i\,\ln\left(i\,x+\sqrt{1-x^2}\right)

Voir aussi

Notes et références

  1. ↑ « Exponentielle & logarithme », § Fonctions circulaires réciproques, Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Arc sinus de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • ARC — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. {{{image}}}   Sigles d une seule lettre   Sigles de deux lettres > Sigles de trois lettres …   Wikipédia en Français

  • sinus — 1. sinus [ sinys ] n. m. • 1539; mot lat. « courbe » → sein ♦ Anat. 1 ♦ Cavité irrégulière (de certains os). Sinus de la face, de certains os de la face (sinus frontal, maxillaire, sinus sphénoïdaux). Spécialt, cour. Inflammation des sinus (de la …   Encyclopédie Universelle

  • arc — 1. arc [ ark ] n. m. • 1080; lat. arcus 1 ♦ Arme formée d une tige souple (de bois, de métal) que l on courbe au moyen d une corde attachée aux deux extrémités pour lancer des flèches. Arc et arbalète. Bander, tendre l arc. Tirer des flèches avec …   Encyclopédie Universelle

  • Arc cosinus — Représentation graphique En mathématiques, l’arc cosinus d un nombre réel compris entre −1 et 1 est l unique mesure d angle dont le cosinus vaut ce nombre, entre l angle nul et l angle plat. La fonction qui associe à tout nombre réel entre −1 et… …   Wikipédia en Français

  • SINUS — s. m. (On prononce l S.) T. de Mathém. La perpendiculaire menée d une des extrémités d un arc, sur le rayon qui passe par l autre extrémité. Table des sinus, des tangentes et des sécantes.   Sinus verse, La partie du rayon comprise entre le sinus …   Dictionnaire de l'Academie Francaise, 7eme edition (1835)

  • Arc — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.   Sigles d’une seule lettre   Sigles de deux lettres > Sigles de trois lettres   Sigles de quatre lettres …   Wikipédia en Français

  • Arc tangente — Représentation graphique En mathématiques, l’arc tangente d un nombre réel est la mesure d un angle orienté dont la tangente vaut ce nombre. La fonction qui à tout nombre réel associe la valeur de son arc tangente en radians est la réciproque de… …   Wikipédia en Français

  • sinus — 1. (si nus ) s. m. 1°   En géométrie, le sinus d un arc ou d un angle est la perpendiculaire abaissée d une extrémité de l arc sur le diamètre qui passe par l autre extrémité. •   Il est indubitable, et en cela Descartes mérite un coup d… …   Dictionnaire de la Langue Française d'Émile Littré

  • sinus-verse — [sinysvɛʀs] n. m. ÉTYM. 1685; de 2. sinus, et verse, adjectif. ❖ ♦ Math. Différence entre le rayon et le cosinus (d un angle, d un arc) …   Encyclopédie Universelle

  • Sinus (mathématique) — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”