- Groupe continu à un paramètre
-
Sous-groupe à un paramètre
Un sous-groupe à un paramètre d'un groupe de Lie réel G est un morphisme de groupes de Lie c:R
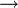 G. Plus explicitement, c est une application différentiable vérifiant :
G. Plus explicitement, c est une application différentiable vérifiant :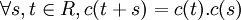 .
.
En dérivant cette relation par rapport à la variable s et en évaluant en s = 0, il vient :
où Lc(t) designe la multiplication à gauche par c(t). Un sous-groupe à un paramètre s'obtient comme orbite de l'élément neutre par un champ de vecteurs invariant à gauche de G. Un tel champ X est déterminé par sa valeur X(e) en l'élément neutre e. Il y a donc correspondance univoque entre sous-groupe à un paramètre et l'espace tangent g de G en e :
- A tout sous-groupe à un paramètre c de G est associé le vecteur c'(0) de g.
- A tout vecteur v de g est associé le sous-groupe à un paramètre c:R
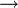 G défini par l'équation différentielle c '(t) = TeLc(t)[v] et la condition initiale c '(0) = v.
G défini par l'équation différentielle c '(t) = TeLc(t)[v] et la condition initiale c '(0) = v.
Les sous-groupes à un paramètre interviennent naturellement dans la définition de l'application exponentielle du groupe de Lie G :
- L'application exponentielle est l'application exp:g
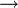 G définie par exp(v)=c(1) où c est le sous-groupe à un paramètre de G associé à X.
G définie par exp(v)=c(1) où c est le sous-groupe à un paramètre de G associé à X. - Tout sous-groupe à un paramètre c s'ecrit de maniere unique c(t)=exp(t.v) ou v = c '(0).
Sommaire
Exemples
Groupe de Lie commutatif
Tout espace vectoriel reel E de dimension finie est un groupe de Lie, la loi interne etant l'addition vectorielle. L'espace tangent en 0 de E s'identifie naturellement avec E en tant qu'espace vectoriel réel. Les sous-groupes à un paramètre de E sont simplement les applications t
 t.v où v parcourt E : ce sont les droites vectorielles paramétrées de E.
t.v où v parcourt E : ce sont les droites vectorielles paramétrées de E.La classification des groupes de Lie commutatifs est connu et élémentaire. Tout groupe de Lie commutatif G se réalise comme quotient d'un espace vectoriel E par un sous-groupe discret, un sous-réseau de E. Les sous-groupes à un paramètre de G s'obtiennent donc par passage au quotient des droites paramétrées de E.
Un exemple important est le tore Rn/Zn. Les sous-groupes à un paramètre sont les applications cv:R
 t.v mod Zn où v parcourt Rn. Apparaissent différents comportements :
t.v mod Zn où v parcourt Rn. Apparaissent différents comportements :- Si v est proportionnel à un élément du réseau Zn, cv est une application périodique, une immersion de la droite réelle, et un difféomorphisme local de R sur un cercle de Rn/Zn.
- Sinon, c est une immersion de la droite réelle, mais l'image n'est pas une variété. En dimension n = 2, l'image est dense dans le tore. En dimension supérieure, l'adhérence de l'image est une sous-variété difféomorphe a un tore, et toutes les dimensions intermédiaires allant de 2 a n sont réalisables.
Groupe des rotations
Pour tout vecteur non nul v de R3, l'application R associant à t la rotation d'axe orienté R.v et d'angle t est un sous-groupe à un paramètre du groupe SO(3) des rotations de l'espace euclidien.
Ce sont exactement tous les sous-groupes à un paramètre de SO(3). Il est remarquable de noter qu'ils sont tous des applications périodiques.
Pour rappel, il est courant de paramétrer le groupe SO(3) par les quaternions unitaires.
Les sous-groupes a un parametre de S3 ont pour images les traces des plans vectoriels reel de H contenant 1. Ce sont des difféomorphismes locaux de R sur des grands cercles de S3.
Groupe à un paramètre de difféomorphismes
La définition se généralise sans difficulté aux groupes de Lie de dimension infinie. L'exemple standard est le groupe des difféomorphismes d'une variété différentielle M de dimension n. Il est loisible d'introduire la notion de groupes à un paramètre de difféomorphismes, par exemple.
Un groupe à un paramètre de difféomorphismes est une application différentiable f:RxM
 M telle que les sections ft soient des difféomorphismes de la variéte M, vérifiant :
M telle que les sections ft soient des difféomorphismes de la variéte M, vérifiant :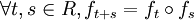 .
.
Un groupe a un parametre de diffeomorphismes de M est tout simplement une action differentiable de R sur M !
Cette notion est à rapprocher de champ de vecteurs :
- A tout groupe a un parametre de diffeomorphisme f de M est associé un unique champ de vecteurs X sur M donné par :
![\forall t\in R, \frac{d}{dt} f_t(x)=X\left[f_t(x)\right]](/pictures/frwiki/99/cc1c7f7ca87c67d007b1d28a9acd82f5.png) .
.
- Reciproquement, si M est compact, à tout champ de vecteurs X sur M est associe un unique groupe a un parametre de diffeomorphismes f déterminé par la relation ci-dessus, et appelé flot du champ X.
Le champ est alors dit global.
Si M possède plus de structures (variété riemannienne, variete symplectique ou variete de contact par exemple), on peut vouloir que les sections ft préservent cette structure. Dans ce cas, on remplace le terme difféomorphisme par un vocabulaire adapté.
References
Liens internes
Liens externes
Bibliographie
- Portail des mathématiques
Catégories : Groupe de Lie | Méthode mathématique de la physique
Wikimedia Foundation. 2010.

![\forall t\in R, c'(t)=T_eL_{c(t)}\left[c'(0)\right]](/pictures/frwiki/99/c3cdaf00d80ef068fc844cc1d7525ee8.png)