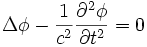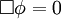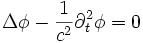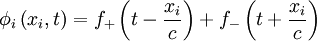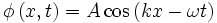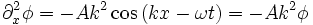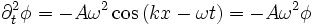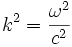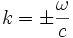Équation de d'alembert

Équation de d'Alembert

En physique, dans l'étude des ondes et de leur propagation, l’équation de d'Alembert décrit la variation dans le temps et dans l'espace d'une quantité ondulant. Elle est nommée d'après Jean le Rond d'Alembert qui l'énonça dans ses Recherches sur les cordes vibrantes^[1] en 1747, comme solution du problème de la corde vibrante. C'est historiquement la première équation d'onde.

Sommaire

1 Énoncé
2 Manifestations et résolution
- 2.1 Solution générale
- 2.2 Solutions harmoniques
3 Notes et références
4 Annexes

Énoncé

Soit $φ$ une quantité, scalaire ou vectorielle, dépendant de la position et du temps. Alors elle vérifie l'équation de d'Alembert lorsque :

$\Delta \phi - \frac{1}{c^2}\frac{\partial^2 \phi}{\partial t^2}=0$

avec Δ l'opérateur laplacien (vectoriel ou non) et c une quantité scalaire positive, appelée vitesse ou célérité de l'onde. On peut encore l'écrire, en introduisant l'opérateur d'alembertien $\Box$ :

$\Box \phi = 0$

ou bien encore :

$\Delta \phi - \frac{1}{c^2} \partial^2_t \phi = 0$

avec la notation courante en électromagnétisme de la dérivée 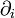$\partial_i$ par rapport à i.

Il s'agit d'une équation de conservation dans l'espace-temps : toute variation dans le temps est compensée par une variation dans l'espace. Elle néglige de fait tout effet diffusif et toute anisotropie. Cette relation étant linéaire, on peut montrer de plus qu'une onde vérifiant l'équation de d'Alembert n'est pas déformée au cours de sa propagation. C'est la plus simple des équations d'onde.

Les cas plus complexes ne peuvent plus être traités par l'équation de d'Alembert, mais par d'autres modèles comme l'équation des télégraphistes par exemple. Leurs solutions ne sont toutefois pas triviales.

Manifestations et résolution

Cette équation différentielle, linéaire, apparaît dans de nombreux phénomènes ondulatoires comme approximation au premier ordre. En particulier, d'Alembert l'appliqua aux mouvements de la corde vibrante.

On peut l'appliquer, moyennant certaines approximations, à l'étude des ondes dans les fluides. En travaillant les équations de Maxwell, on montre que les champs électrique et magnétique vérifient une équation de d'Alembert, propageant ainsi une onde électromagnétique : la lumière.

Solution générale

Les solutions de l'équation de d'Alembert sont exactement les fonctions $φ$ , dont la projection sur chacun des axes de coordonnés est de la forme :

$\phi_i \left( x_i, t \right) = f_{+} \left( t - \frac{x_i}{c} \right) + f_{-} \left( t + \frac{x_i}{c} \right)$

avec x_i chacune des coordonnées, t le temps et c la vitesse de l'onde. Les deux fonctions f₊ et f_- ne dépendent que d'une variable et sont définies à partir des conditions initiales.

Elles représentent respectivement une onde se propageant sans se déformer vers +∞ et une onde se propageant sans se déformer vers -∞.

Solutions harmoniques

L'équation de d'Alembert étant par ailleurs linéaire, on peut sans restriction considérer uniquement les solutions sinusoïdales, dites harmoniques ou monochromatiques. En effet, toute configuration peut être ramenée à une somme de sinusoïdes par la transformée de Fourier.

Supposons l'onde unidimensionnelle, selon x, se propageant vers +∞. On peut l'écrire :

$\phi \left( x, t \right) = A \cos \left( kx - \omega t \right)$

avec k le nombre d'onde, A l'amplitude et ω la pulsation.

En dérivant deux fois par rapport à x, on obtient :

$\partial^2_x \phi = - A k^2 \cos \left( kx - \omega t \right) = -A k^2 \phi$

En dérivant deux fois par rapport à t, on obtient :

$\partial^2_t \phi = - A \omega^2 \cos \left( kx - \omega t \right) = -A \omega^2 \phi$

Elle vérifie donc l'équation de d'Alembert à la seule condition que :

$k^2 = \frac{\omega^2}{c^2}$

et c comme ω sont des quantités positives, donc cela équivaut à :

$k = \pm \frac{\omega}{c}$

Cette dernière relation est appelée relation de dispersion.

Appliquée aux conditions initiales, cette décomposition en sinusoïdes permet notamment l'étude analytique de la propagation des ondes, ou la simulation informatique de tels phénomènes.

Notes et références

↑ Jean LE ROND D’ALEMBERT, Recherches sur la courbe que forme une corde tenduë mise en vibration, Histoire de l’Académie des Sciences et Belles-Lettres de Berlin année 1747, Berlin, 1749, p. 214-249

Annexes

Liens externes

http://www.europeana.eu/, bibliothèque virtuelle européenne

Bibliographie

Jean LE ROND D’ALEMBERT, Articles extraits de l'Histoire de l’Académie des Sciences et Belles-Lettres de Berlin année 1747, Berlin, 1749

Portail de la physique

Ce document provient de « %C3%89quation de d%27Alembert ».

Catégorie : Mécanique ondulatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation de d'alembert de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Equation de d'Alembert — Équation de d Alembert En physique, dans l étude des ondes et de leur propagation, l’équation de d Alembert décrit la variation dans le temps et dans l espace d une quantité ondulant. Elle est nommée d après Jean le Rond d Alembert qui l énonça… … Wikipédia en Français
Équation de d'Alembert — En physique, dans l étude des ondes et de leur propagation, l’équation de d Alembert décrit la variation dans le temps et dans l espace d une quantité ondulant. Elle est nommée d après Jean le Rond d Alembert qui l énonça dans ses Recherches sur… … Wikipédia en Français
Equation d'onde — Équation d onde L équation d onde est l équation générale qui décrit la propagation d une onde, qui peut être représentée par une grandeur scalaire ou vectorielle. Dans le cas vectoriel, en espace libre, dans un milieu homogène, linéaire et… … Wikipédia en Français
Équation de propagation des ondes — Équation d onde L équation d onde est l équation générale qui décrit la propagation d une onde, qui peut être représentée par une grandeur scalaire ou vectorielle. Dans le cas vectoriel, en espace libre, dans un milieu homogène, linéaire et… … Wikipédia en Français
Alembert — Jean le Rond D Alembert D’Alembert Nom de naissance Jean le Rond d’Alembert Naissance 16 novembre 1717 Paris D … Wikipédia en Français
Équation d'onde — L équation d onde est l équation générale qui décrit la propagation d une onde, qui peut être représentée par une grandeur scalaire ou vectorielle. Dans le cas vectoriel, en espace libre, dans un milieu homogène, linéaire et isotrope, l équation… … Wikipédia en Français
Equation — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation (mathématiques) — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation symétrique — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation vectorielle — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Équation de d'alembert