- Équation de Nernst (électrophysiologie)
-
Potentiel électrochimique de membrane
Toute cellule est entourée d'une membrane. Cette membrane, constituée d'une bicouche lipidique phospholipidique et de protéines insérées, est relativement imperméable aux molecules polaires telles que l'eau et aux espèces chargées telles que les ions. Elle présente une grande résistance électrique. Grâce à ces propriétés, elles sépare en deux compartiments étanches l'intérieur de la cellule, le cytoplasme, de l'extérieur de la cellule, le milieu extracellulaire. De par l'activité permanente des protéines membranaires, la composition ionique de ces deux compartiments est différente. C'est pourquoi il existe pour chacun des composés ioniques dont la concentration est différente un potentiel électrochimique.
Équation de Nernst : Potentiel électrochimique pour chaque composé ionique
Soient deux compartiments de même volume contenant de l'eau pure et séparés par une membrane poreuse. Dans le compartiment A, on dissous une quantité de sel de cuisine (NaCl) et on laisse le compartiment B inchangé. Le sel se dissocie entièrement en Na+ et Cl- dans le compartiment A. La première loi de diffusion de Fick prédit qu'un flux de Na+ et Cl- va avoir lieu depuis le compartiment A vers le compartiment B jusqu’à équilibration des concentrations en Na+ et Cl- dans les deux compartiments. Afin de fixer les idées, si on introduit 1 mole de NaCl dans le compartiment A, à l'équilibre, il y aura 0.5 mole de NaCl dans chaque compartiment. Il s'agit du principe fondamental de la dialyse effectuée sur les insuffisants rénaux.
Supposons maintenant que la membrane ait des pores qui ne laissent passer que les ions Na+. On réitere l'expérience. On constate alors que la concentration en sel du compartiment B reste nulle. Si on place une électrode de mesure dans chaque compartiment, on remarque qu'une différence de potentiel entre le compartiment A et le compartiment B s'est établie. L'explication est la suivante : Les ions Na+ diffusent de A vers B. Au niveau de la membrane, les ions Na+ traversent, mais pas les ions Cl-. Une accumulation de charge négatives (Cl-) se fera du côté A et une accumulation de charges positives (Na+) se fera du côté B. Le champ électrique créé par cette séparation de charge s'oppose à toute sortie supplémentaire d'ions Na+. En fait, la diffusion continue mais elle est compensée exactement par une migration imposée par le champ électrique, il s'agit d'un équilibre dynamique. La valeur de la différence de potentiel entre les compartiments A et B est donnée par l'équation de Nernst.
où :
- Ei est le potentiel électrique du compartiment i
- [I]i la concentration de l'espèce perméante I du compartiment i (dans notre exemple Na+)
- R la constante des gaz parfaits
- T la température en kelvin
- z la charge de l'ion perméant (avec le signe)
- F la constante de Faraday
- (F = 96 485 C.mol-1 = N e où N est le nombre d'Avogadro et e la charge élémentaire de l'électron)
- ln le logarithme népérien.
Pour l'équation de Nernst telle qu'utilisée en électrochimie, voir Équation de Nernst.
Équation de Goldman-Hodgkin-Katz : Potentiel électrochimique pour plusieurs composé ioniques localement
L'Équation de Goldman-Hodgkin-Katz en voltage donne la valeur du potentiel de membrane lorsque plus d'une conductance est active au sein de la membrane considérée. Il s'agit typiquement du cas du neurone lors du potentiel d'action, mais aussi le cas de la majorité des cellules lorsque l'hypothèse simplificatrice de la seule activité de canaux potassiums n'est pas posée. On remarque en effet que la valeur mesurée du potentiel de membrane diffère de la valeur théorique donné par l'équation de Nernst appliquée au potassium.
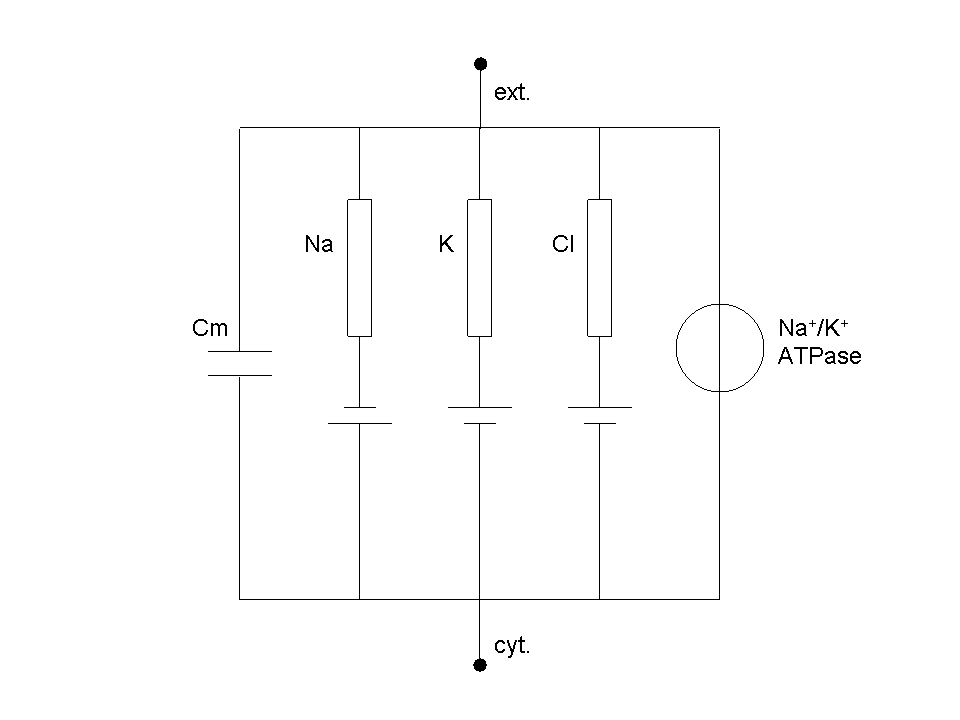 Schéma électrique équivalent de la cellule
Schéma électrique équivalent de la cellule
Équivalent électrique de la cellule
La cellule peut être décrite par un schéma électrique équivalent (voir figure ci contre). On y distingue :
- Cm, la capacité de la membrane, égale à 1 µF.cm-2, directement proportionnel à la surface de membrane
- les diverses conductances (rectangles) qui sont en général variables dans le temps
- les piles électrochimiques associées (donné par l'équation de Nernst)
- le générateur de tension (pompes membranaires, en particulier l'ubiquitaire Na/K ATPase)
Théories des cables : propagation de potentiel le long de la membrane
L'axone du neurone est un prolongement cellulaire comportant des canaux ioniques en grande quantité. L'activité des canaux est responsable de la propagation de l'influx nerveux.
L'équivalent électrique de l'axone est une juxtaposition parallèle d'équivalents électriques reliés entre eux par une résistance longitudinale.
Propagation simple
Propagation saltatoire
Rôles physiologiques
L'existence d'un potentiel électrochimique de part et d'autre de la membrane plasmique est universelle parmi les cellules. Il est maintenu activement par des pompes ioniques, pompe sodium/potassium chez les cellules animales, pompes à protons chez les cellules végétales et les champignons. Il constitue une énergie potentielle qui est utilisée pour transporter plusieurs petites molécules contre leur gradient de concentration. Les nutriments (composés nécessaires au métabolisme cellulaire) sont importés, tandis que les déchets du métabolisme sont exportés.
Le potentiel électrochimique de membrane constitue aussi la force motrice nécessaire au courant potassique de fuite qui définit le potentiel de repos d'une cellule excitable, ainsi qu'aux courants sodiques, calciques et potassiques activés pendant un potentiel d'action ou un potentiel postsynaptique.
Au niveau de la sous-compartimentation de la cellule, d'autres potentiels électrochimiques sont maintenus en permanence :
- entre les compartiments des organites producteurs d'énergie, les mitochondries et les chloroplastes
- de part et d'autre des membranes des réticulum endoplasmiques, en particulier les calciosomes remplis de calcium
- dans certaines vésicules à pH bas
Différence de concentration ionique de part et d'autre de la membrane
Les concentrations physiologiques des principaux ions chez l'homme Ion concentration intracellulaire (mmol/l) concentration extracellulaire (mmol/l) Rapport Potentiel d'équilibre d'après l'équation de Nernst Na+ 7-12 144 1:12 env. +60 mV K+ 160 4 40:1 -91 mV Ca2+ 10-5-10-4 2 +125 mV à +310 mV Cl- 4-7 120 -82 mV HCO3- 8-10 26-28 -27 mV Protéine anionique (chargée négativement) 155 5 Dans l'axone géant de calmar Ion concentration intracellulaire (mmol/l) concentration extracellulaire (mmol/l) Rapport Potentiel d'équilibre d'après l'équation de Nernst Na+ 50 440 1:8 +55 mV K+ 400 2 200:1 -75 mV Ca2+ 10-7 14 +149 mV Cl- 52 560 -60 mV HCO3- Protéine anionique (chargée négativement) (source : Neurowissenschaft, Dudel, Menzel, Schmidt, 2°édition, 2001, p.67
muscles squelettiques des animaux à sang chaud Ion concentration intracellulaire (mmol/l) concentration extracellulaire (mmol/l) Rapport Potentiel d'équilibre d'après l'équation de Nernst Na+ 12 145 1:12 +67 mV K+ 155 4 39:1 -98 mV Ca2+ 10-7 1,5 +129 mV Cl- 4 123 -90 mV HCO3- Protéine anionique (chargée négativement) 155 (source : Neurowissenschaft, Dudel, Menzel, Schmidt, 2°édition, 2001, p.67)
Notes et références de l'article
Voir aussi
Articles connexes
Liens et documents externes
- Portail de la biologie
Catégorie : Électrophysiologie
Wikimedia Foundation. 2010.

![V_m = E_A - E_B = \frac{-RT}{zF} \ln\frac{[I]_{\mbox{A}}}{[I]_{\mbox{B}}}](/pictures/frwiki/49/183e76ee4e580922d11672ec9e1c02d9.png)