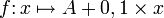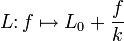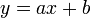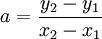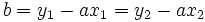- Équation affine
-
Fonction affine
En mathématiques élémentaires, une fonction affine est une fonction de la variable réelle dont la représentation graphique est une droite. C'est une fonction polynôme de degré inférieur ou égal à 1. Elle est de la forme :
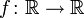
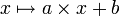avec a et b des nombres réels fixés.
Dans l'expression ci-dessus, a et b sont des constantes et x est la variable.
La constante a est appelée coefficient directeur et b ordonnée à l'origine.
Si a est nul, alors la fonction est constante.
Si b est nul alors la fonction est linéaire et sa droite représentative passe par l'origine.
Sommaire
Propriété caractéristique
Une fonction affine est caractérisée par le fait que son taux d'accroissement est constant. En effet, si x₁ et x₂ sont deux réels, l'accroissement f(x₁) − f(x₂) est proportionnel à x₁ − x₂, comme le donne l’égalité :
- f(x₁) − f(x₂) = a (x₁ − x₂).
Cette propriété donne alors un outil pour déterminer le coefficient a :
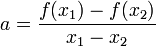si x₁ ≠ x₂.
Par conséquent, la dérivée d'une fonction affine est une fonction constante : le coefficient directeur de la fonction affine.
L'ordonnée à l'origine b peut se calculer de la manière suivante :
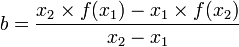si x₁ ≠ x₂.
Exemples
On rencontre quelques exemples de fonctions affines dans
- les abonnements téléphoniques. Le prix de l'abonnement mensuel est A et le prix d'une communication à la minute est de 0,10 €/min. La facture téléphonique est alors une fonction affine du nombre x de minutes de communication dans le mois :
- La longueur d'un ressort. Si au repos le ressort a une longueur L₀ et si sa raideur est k, alors la longueur du ressort est une fonction affine de la force appliquée (loi de Hooke).
- Dans ce cas, le coefficient directeur est 1/k et l'ordonnée à l'origine L₀.
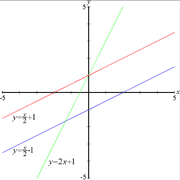
Représentation graphique
La représentation graphique d'une fonction affine est une droite dont l'équation est
La droite coupe l'axe des ordonnées pour y = b (d'où le nom : ordonnée à l'origine). Lorsque b est égal à 0, la droite passe par l'origine du repère cartésien.
La droite a pour pente ou coefficient directeur le réel a. Si a>0, la fonction affine est croissante (la droite « monte ») et si a<0, elle est décroissante (la droite « descend »). Par un processus analogue à celui vu pour la fonction linéaire, un déplacement d’un carreau en abscisse induit un déplacement de a carreaux en ordonnée, si le repère est orthonormé.
Détermination de a et b
Si M(x₁,y₁) et N(x₂,y₂) sont deux points appartenant à la droite d'équation y = ax + b, alors on a :
Médias
Voir aussi
Portail des mathématiques
Catégorie : Analyse
Wikimedia Foundation. 2010.
