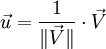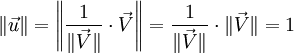Vecteur normalisé

Vecteur normalisé

Vecteur unitaire

Dans un espace vectoriel normé, un vecteur unitaire est un vecteur dont la norme est égale à 1.

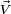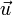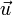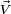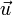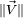Ce type de vecteur est utilisé pour caractériser la direction d'un vecteur quelconque. Ainsi, on peut exprimer un vecteur \scriptstyle\vec V en fonction d'un vecteur unitaire \vec u par la multiplication par un scalaire de \vec u et de la norme de \scriptstyle\vec V (on « étire » \vec u d'un facteur \scriptstyle\|\vec V\|) :

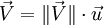\vec V = \|\vec V\| \cdot \vec u.

Pour rendre un vecteur 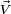\scriptstyle\vec V unitaire, on le multiplie donc par l'inverse de sa norme.

\vec u = \frac 1 {\|\vec V\|}\cdot\vec V


Démonstrations
\|\vec u\| = \left\| \frac{1}{\|\vec V\|} \cdot \vec V \right\| = \frac{1}{\|\vec V\|} \cdot \|\vec V\| = 1

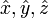En physique, pour dénoter les vecteurs unitaires, il est usuel d'utiliser un accent circonflexe: \hat{x}, \hat{y}, \hat{z} .

Dérivation des vecteurs unitaires

Soit une fonction dérivable 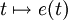t\mapsto e(t) à valeurs dans un espace euclidien E, telle que pour tout t, e(t) est un vecteur unitaire. Alors le vecteur dérivé e'(t) est orthogonal à e(t). En effet, il suffit de dériver l'expression du carré de la norme, sachant que celle-ci est constante – donc de dérivée nulle – et que le produit scalaire s'annule justement pour deux vecteurs orthogonaux :

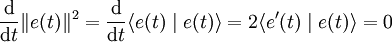\frac{\mathrm d}{\mathrm dt}\|e(t)\|^2 = \frac{\mathrm d}{\mathrm dt}\langle e(t)\mid e(t)\rangle = 2\langle e'(t)\mid e(t)\rangle=0.

C'est le cas notamment pour les vecteurs de toutes les bases orthonormales mobiles.

Liens internes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Vecteur unitaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Vecteur normalisé de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Vecteur de Laplace-Runge-Lenz — Vecteur de Runge Lenz Dans cet article les vecteurs et leurs normes sont indiqués respectivement en gras et italique. Par exemple : . En mécanique classique, le vecteur de Runge Lenz ou invariant de Runge Lenz est un vecteur utilisé… …   Wikipédia en Français

  • Vecteur de Runge-Lenz — Dans cet article les vecteurs et leurs normes sont indiqués respectivement en gras et italique. Par exemple : . En mécanique classique, le vecteur de Runge Lenz ou invariant de Runge Lenz est un vecteur utilisé principalement pour décrire la …   Wikipédia en Français

  • Normalisé — Norme Pour les articles homonymes, voir Norme (homonymie). Une du latin norma, « équerre, règle ») désigne un état habituellement répandu ou moyen considéré le plus souvent comme une règle à suivre. Ce terme générique désigne un… …   Wikipédia en Français

  • Décomposition en valeurs singulières — En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des matrices rectangulaires réelles ou… …   Wikipédia en Français

  • Arc rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une …   Wikipédia en Français

  • Courbe rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une …   Wikipédia en Français

  • Identite de polarisation — Identité de polarisation En mathématiques, l identité de polarisation concerne l algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des… …   Wikipédia en Français

  • Identité De Polarisation — En mathématiques, l identité de polarisation concerne l algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des applications de ExE dans le …   Wikipédia en Français

  • Identité de polarisation — En mathématiques, les identités de polarisation concernent l algèbre multilinéaire. Elles correspondent à une caractérisation des formes bilinéaires symétriques, des formes hemitiennes et des formes sesquilinéaires. Si E est un espace vectoriel,… …   Wikipédia en Français

  • Longueur D'un Arc — Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une trajectoire d un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”