Trigonométrie sphérique

Trigonométrie sphérique

La trigonométrie sphérique est un ensemble de relations analogues à celles de la trigonométrie euclidienne mais portant sur les angles et distances repérés sur une sphère.

La figure de base est le triangle sphérique, délimité non plus par des segments de droites mais par des arcs de grands cercles de cette sphère. Les règles habituelles de la trigonométrie euclidienne ne sont pas applicables ; par exemple la somme des angles d'un triangle situé sur une sphère est supérieure à 180 degrés.

Sommaire

Le triangle sphérique

Formules fondamentales

triangle sphérique

Conventions

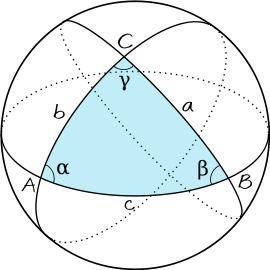
On considère trois points A, B et C sur une sphère comme représentés par la figure ci-contre, ainsi que les arcs de grands cercles qui les relient. On note α, parfois ^{\hat A}, l'angle du triangle au sommet A, et de façon analogue pour les autres sommets. On note a, b et c les angles sous-tendus au centre O de la sphère par la partie de grand cercle correspondante. Ainsi a désigne l'angle BOC, etc. Un angle de 2π correspond à un grand cercle entier. Bien entendu les longueurs se déduisent de a, b et c en les multipliant par le rayon de la sphère.

Formule des cosinus et relation duale

L'une des relations les plus importantes de la trigonométrie sphérique, donnée par François Viète en 1593 dans son De Varorium[1] est la formule des cosinus, qui relie la longueur d'un côté à celles de deux autres côtés ainsi qu'à l'angle entre eux :

\cos c = \cos a\, \cos b + \sin a\, \sin b\, \cos\gamma~,

qu'il ne faut pas confondre avec la relation duale, obtenue en remplaçant dans cette relation tous les grands cercles par leurs points polaires :

\cos\gamma = -\cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta\,\cos c~.

La formule des cosinus se démontre de plusieurs façons. L'une d'elle consiste à exprimer de différentes manières le produit scalaire, dans l'espace euclidien ambiant, entre les vecteurs reliant le centre O de la sphère aux points A et B. Une autre est détaillée ci dessous.

Dans le cas particulier où le triangle est rectangle en C, on obtient

\cos\, c = \cos\, a \cos\, b,

formule correspondant au théorème de Pythagore pour la trigonométrie sphérique. On remarque que si le triangle est suffisamment petit pour que l'on puisse remplacer les cosinus par leur développement limité au deuxième ordre, on retrouve effectivement le théorème de Pythagore.

La formule des cosinus permet notamment de calculer la distance entre deux points A et B sur la Terre en fonction de leurs latitudes et longitudes. Pour cela, on place C au pôle nord, de sorte que a est le complémentaire de la latitude \scriptstyle{\phi_A} de A, b le complémentaire de celle \scriptstyle{\phi_B} de B, et c la différence de longitude \scriptstyle{\Delta \lambda = \lambda_B - \lambda_A}. On obtient directement

d_{AB}=R c= R \arccos{ \left( \sin \phi_A \sin \phi_B + \cos \phi_A \cos \phi_B \cos \Delta \lambda \right)} (où R = 6400 km est le rayon terrestre).

La relation peut également s'écrire sous la forme

\cos\gamma = \frac{\cos c - \cos a\,\cos b}{\sin a\,\sin b}~.

Des expressions analogues pour cosα et cosβ on déduit la troisième formule fondamentale de la trigonométrie sphérique (les deux premières étant celles des cosinus et des sinus) :

\sin b\cos\alpha+\cos c\sin a\cos\beta=\sin c\cos a~.

La relation duale peut quant à elle s'écrire

\cos c = \frac{\cos\gamma + \cos\alpha\,\cos\beta}{\sin\alpha\,\sin\beta}~.

Formule des sinus

On remarque que d'après la relation duale évoquée précédemment, un triangle sphérique est déterminé par ses trois angles, ce qui est très différent du cas du triangle euclidien (plan). Il y a une analogie parfaite (de dualité), dans le triangle sphérique, entre longueurs des côtés et angles aux sommets. La formule des sinus illustre cette analogie :

\frac{\sin a}{\sin \alpha} = \frac{\sin b}{\sin \beta} = \frac{\sin c}{\sin \gamma}~,

ou encore

\sin a : \sin b : \sin c = \sin\alpha : \sin\beta : \sin\gamma~,

ce qui doit se comprendre comme « les trois quantités de gauche sont dans les mêmes proportions que les trois quantités de droite (le rapport entre deux quelconques à gauche est le même que le rapport correspondant à droite) ».

Démonstration des formules fondamentales

a, b et c désignent les longueurs, A, B et C désignent les sommets, α, β et γ désignent les angles du triangle sphérique.

1) On forme deux repères orthonormés directs R et R' de même premier vecteur, et tels que A soit le pôle nord du système de coordonnées sphériques associé au premier repère et B le pôle nord du second.
Détail de cette construction

On note R=(O,\overrightarrow i,\overrightarrow j,\overrightarrow k) et R'=(O,\overrightarrow {i'}, \overrightarrow{j'}, \overrightarrow{k'}) avec \overrightarrow k= \overrightarrow{OA},~ \overrightarrow{k'}= \overrightarrow{OB}~.

On prend alors

\overrightarrow i=\overrightarrow {i'}={ 1\over \sin c } \overrightarrow k\wedge \overrightarrow {k'}={ 1\over \sin c } \overrightarrow{OA}\wedge \overrightarrow{OB}~.

On en déduit

\overrightarrow j= \overrightarrow k\wedge \overrightarrow i= { 1\over \sin c } [ \overrightarrow{OA}\wedge(\overrightarrow{OA}\wedge \overrightarrow{OB})]~.

La formule du double produit vectoriel conduit à

\overrightarrow j={ 1\over \sin c } ( (OA|OB)\overrightarrow{OA}-||OA||^2\overrightarrow{OB})={1\over \sin c } (\cos c~\overrightarrow{OA}-\overrightarrow{OB})~.

De même,

\overrightarrow{j'}= { 1\over \sin c } [ \overrightarrow{OB}\wedge(\overrightarrow{OA}\wedge \overrightarrow{OB})]= {1\over \sin c } ( \overrightarrow{OA}-\cos c~ \overrightarrow{OB})~.
2) Le changement de repère (de R vers R') est une rotation dans l'espace autour de l'axe commun aux deux repères. Comme l'angle entre \overrightarrow{OA} et \overrightarrow{OB} est c, on en déduit que la matrice de passage est
P=\begin{pmatrix} 1&0&0\\ 0& \cos c&-\sin c\\ 0&\sin c &\cos c \end{pmatrix}~.
3) On donne maintenant les coordonnées de C dans le repère R.
On remarque que b est la colatitude dans le repère sphérique de pôle nord A associé au repère cartésien, alors que α désigne l'angle (au pôle) entre le vecteur -\overrightarrow j et le demi-plan vertical (A,O,C), donc la longitude vaut α-(π/2).
On en déduit que C, de coordonnées sphériques [1,\alpha-{\pi\over 2},b ], a pour coordonnées cartésiennes dans le premier repère
X=\begin{pmatrix}\sin b\sin \alpha \\ -\sin b\cos \alpha\\ \cos b \end{pmatrix}~.
4) On donne de même les coordonnées de C dans le second repère R'.
Cette fois, le pôle nord est le point B, la colatitude est a, et β est l'angle que fait le demi-plan vertical (B,O,C) avec le vecteur \overrightarrow{j'}, donc la longitude vaut (π/2)-β.
On en déduit que C, de coordonnées sphériques [1,{\pi\over 2}-\beta,a ], a pour coordonnées cartésiennes dans le second repère
X'= \begin{pmatrix} \sin a\sin\beta \\ \sin a\cos\beta\\ \cos a \end{pmatrix}~.
5) La formule de changement de base s'écrit alors :
\begin{pmatrix} \sin b\sin \alpha \\ -\sin b\cos \alpha\\ \cos b \end{pmatrix}=X=PX'=\begin{pmatrix} 1&0&0\\ 0& \cos c&-\sin c\\ 0&\sin c &\cos c \end{pmatrix} \begin{pmatrix}\sin a\sin \beta \\ \sin a\cos \beta\\ \cos a \end{pmatrix}~.
On en déduit d'un seul coup la formule des sinus, la troisième formule fondamentale de la trigonométrie sphérique et la formule des cosinus :
\begin{cases} \sin b \sin \alpha= \sin a \sin \beta \\ \sin b \cos \alpha=\sin c\cos a-\cos c\sin a\cos\beta\\ \cos b= \sin c \sin a \cos \beta +\cos c\cos a~.\end{cases}

Autres formules

Formules des demi-angles et demi-côtés

Soit \scriptstyle{ s=\frac1 2 (a+b+c)} le demi-périmètre du triangle. Alors on a

\tan^2\frac{\gamma}{2} = \frac{\sin(s-a)\,\sin(s-b)}{\sin s\,\sin(s-c)}

et pour les formules duales, avec \scriptstyle{ \sigma =\frac1 2(\alpha+\beta+\gamma)} :

tan^2\frac{c}{2} = - \frac{\cos\sigma\,\cos(\sigma-\gamma)}{\cos(\sigma-\alpha)\, \cos(\sigma-\beta)}.

Ces formules qui, comme la relation fondamentale, lient un angle au centre aux trois côtés du triangle sphérique ne contiennent pas de somme. Elles étaient très utilisées pour les calculs pratiques à l'aide de tables de logarithmes.

Formules de Gauss

On a \frac{\cos\frac{a+b}{2}}{\cos\frac{c}{2}} = \frac{\cos\frac{\alpha+\beta}{2}}{\sin\frac{\gamma}{2}} et \frac{\sin\frac{a+b}{2}}{\sin\frac{c}{2}} = \frac{\cos\frac{\alpha-\beta}{2}}{\sin\frac{\gamma}{2}} ainsi que \frac{\cos\frac{a-b}{2}}{\cos\frac{c}{2}} = \frac{\sin\frac{\alpha+\beta}{2}}{\cos\frac{\gamma}{2}} et \frac{\sin\frac{a-b}{2}}{\sin\frac{c}{2}} = \frac{\sin\frac{\alpha-\beta}{2}}{\cos\frac{\gamma}{2}}~.

On en déduit la loi des tangentes en trigonométrie sphérique :

\frac{\tan\frac{a-b}2 }{\tan\frac{a+b}2 } = \frac{\tan\frac{\alpha-\beta}2 }{\tan\frac{\alpha+\beta}2}~.

Analogies de Napier

Elles s'obtiennent en combinant deux à deux les formules de Gauss :

  • \tan\frac{c}{2} \cos\frac{\alpha-\beta}{2} = \tan\frac{a+b}{2} \cos\frac{\alpha+\beta}{2}
  • \tan\frac{c}{2} \sin\frac{\alpha-\beta}{2} = \tan\frac{a-b}{2} \sin\frac{\alpha+\beta}{2}
  • \cot\frac{\gamma}{2} \cos\frac{a-b}{2} = \tan\frac{\alpha+\beta}{2} \cos\frac{a+b}{2}
  • \cot\frac{\gamma}{2} \sin\frac{a-b}{2} = \tan\frac{\alpha-\beta}{2} \sin\frac{a+b}{2}

Aire du triangle sphérique

En anglais, elle est connue sous le nom de formule de Girard. De façon remarquable, l'aire du triangle sphérique se calcule très simplement à partir de ses trois angles : elle est exactement égale à son « défaut d'euclidianité » (différence entre la somme des angles du triangle et π) multiplié par le carré du rayon R de la sphère. Soit :

^{S=(\hat A+\hat B+\hat C-\pi)R^2=R^2\varepsilon }

Remarque : ε est un angle solide s'exprimant en stéradians (pour ^{\hat A, \hat B} et ^{\hat C} exprimés en radians). Cette formule se montre de façon élémentaire[2]. Elle se fait en trois étapes :

  • Lorsque la sphère est découpée en 4 secteurs (« fuseaux » ou « lunes » chez Legendre) par deux plans diamétraux, l'aire d'un des secteurs ainsi découpé est proportionnelle à l'angle ^{\hat A} des deux plans. Elle vaut donc
    ^{2\hat AR^2}.
  • Les trois plans diamétraux qui définissent un triangle sphérique découpent sur la sphère douze fuseaux dont six contiennent ce triangle ou son symétrique, de même aire, par rapport au centre la sphère. Ces six fuseaux recouvrent la sphère, le triangle et son symétrique étant recouverts trois fois chacun, le reste ne l'étant qu'une seule fois. Ainsi, la somme des aires des six fuseaux est celle de la sphère augmentée quatre fois de celle du triangle. Il s'en déduit :
^{2(2\hat AR^2+2\hat BR^2+2\hat CR^2)=4\pi R^2+4S}.
  • Ainsi, après transformation :
^{S=(\hat A+\hat B+\hat C-\pi)R^2}

Cette formule, découverte par Thomas Harriot, mais non publiée, fut donnée pour la première fois par Albert Girard vers 1625.

Formule de l'Huilier

Cette formule est analogue à la formule de Héron qui calcule l'aire d'un triangle euclidien en fonction de ses côtés, et elle fait la même chose pour le triangle sphérique :

\tan\frac{s}{2} \tan\frac{s-a}{2} \tan\frac{s-b}{2} \tan\frac{s-c}{2} = \tan^2\frac{\varepsilon}{4}

(on rappelle qu'on a appelé s=(a+b+c)/2 le demi-périmètre).

Aperçu historique

La trigonométrie, et en particulier la trigonométrie sphérique, doit beaucoup aux astronomes et mathématiciens grecs Hipparque de Nicée[3] ainsi que Ménélaos d'Alexandrie, mais aussi aux mathématiciens persans de langue arabe et indiens. Parmi les plus célèbres figurent Al Biruni, Abu Nasr Mansur et Bhāskara II. Le premier traité de trigonométrie sphérique semble avoir été écrit vers 1060 par Al-Jayyani (en), un mathématicien de l'Andalousie alors sous domination musulmane.

Applications

Calculs de coordonnées :

Notes et références

  1. ↑ Michel Chasles : Mémoires sur les questions proposées par l'Académie royale des sciences de Bruxelles page 54.
  2. ↑ Quelques explications sur le site du Palais de la découverte
  3. ↑ Œuvres complètes de François Arago. François Arago, tome 3, page 158 (Gide, Paris - 1855).

Voir aussi

Articles connexes

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Trigonométrie sphérique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Trigonometrie spherique — Trigonométrie sphérique La trigonométrie sphérique est un ensemble de relations analogues à celles de la trigonométrie euclidienne mais portant sur les angles et distances repérés sur une sphère. Les règles habituelles de la trigonométrie… …   Wikipédia en Français

  • trigonométrie — [ trigɔnɔmetri ] n. f. • 1613; lat. sc. trigonometria (1595); cf. trigone et métrie 1 ♦ Sc. Branche des mathématiques dont le principal objet est l application du calcul à la détermination des éléments des triangles, au moyen des fonctions… …   Encyclopédie Universelle

  • sphérique — [ sferik ] adj. • 1555; sperique 1370; bas lat. sphæricus 1 ♦ En forme de sphère. ⇒ rond. Une bille parfaitement sphérique. Une boule à peu près sphérique ⇒ sphéroïdal. 2 ♦ Géom. Qui appartient à la sphère. Anneau, calotte, secteur, segment… …   Encyclopédie Universelle

  • Trigonometrie — Trigonométrie Planche sur la Trigonométrie, 1728 Cyclopaedia La trigonométrie (du grec ancien τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations… …   Wikipédia en Français

  • trigonometrie — TRIGONOMETRIE. s. f. La partie de la Geometrie, qui enseigne à mesurer les triangles. Il entend bien la trigonometrie. la connoissance de la trigonometrie est fort necessaire aux Arpenteurs. trigonometrie spherique. la connoissance de la… …   Dictionnaire de l'Académie française

  • Trigonométrie — Planche sur la Trigonométrie, 1728 Cyclopaedia. La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et… …   Wikipédia en Français

  • sphérique — (sfé ri k ) adj. 1°   Qui est rond comme une sphère. •   Enfin la raison et le voyage de Christophe Colomb rendirent à la terre son ancienne forme sphérique, VOLT. Phil. Newt. III, 9. •   Pourquoi une goutte d eau est elle sphérique ? c est que,… …   Dictionnaire de la Langue Française d'Émile Littré

  • SPHÉRIQUE — adj. des deux genres Qui a la forme d’une sphère. Corps sphérique. Figure sphérique. Ballon sphérique et, substantivement, Sphérique, Aérostat en forme de sphère. SPHÉRIQUE signifie aussi, surtout en termes de Géométrie, Qui appartient à la… …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • TRIGONOMÉTRIE — s. f. La partie de la géométrie qui enseigne à calculer tous les éléments d un triangle, quand un certain nombre de ces éléments sont donnés. Trigonométrie rectiligne, Celle qui enseigne à calculer les triangles rectilignes ; et, Trigonométrie… …   Dictionnaire de l'Academie Francaise, 7eme edition (1835)

  • trigonométrie — (tri go no mé trie) s. f. Science qui a pour objet de résoudre les triangles, c est à dire d en déterminer par le calcul les angles et les côtés en partant de certaines données numériques. •   Il [Hipparque] a entrepris et exécuté la vraie… …   Dictionnaire de la Langue Française d'Émile Littré

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”