Iconographie des corrélations

En analyse des données, l'iconographie des corrélations^[1] est une méthode qui consiste à remplacer une matrice de corrélation par un schéma où les corrélations « remarquables » sont représentées par un trait plein (corrélation positive), ou un trait pointillé (corrélation négative).

Cette idée apparaît aussi dans les modèles graphiques gaussiens utilisés notamment en cartographie du génome. Mais l’iconographie des corrélations est plus générale en ce qu’elle ne fait pas d’hypothèse sur la distribution gaussienne, ou non, des variables, et repose uniquement sur l’aspect géométrique du coefficient de corrélation.

Sommaire 1 Historique 2 Qu’est-ce qu’une corrélation « remarquable » ? 3 Sélection des liens remarquables 4 Instants remarquables de l’analyse 5 Algorithme de l’iconographie des corrélations 6 Position des points sur le papier 7 Choix du seuil 8 Organisation des liens 9 Retrait d’une influence évidente 10 Interactions logiques remarquables 11 Base de connaissance associée au schéma 12 Champs d’application de l’iconographie des corrélations 12.1 Un moyen de ne rien oublier d’essentiel dans un tableau de donnée 12.2 L’analyse des grands tableaux de bord 12.3 Une alternative à la stratification 13 Voir aussi 14 Références

Historique

L’idée première de l’iconographie des corrélations remonte à 1975. Appliquée d’abord à la géochimie marine, elle fit l’objet d’une thèse d’état en 1981, et d’un article dans les Cahiers de l’Analyse des Données en 1982^[2]. Après cela, l’application de la méthode dans de nombreuses branches de l’industrie aérospatiale^[3],[4] pendant une quinzaine d’année, explique, paradoxalement, la relative confidentialité dans laquelle elle est restée longtemps, les entreprises ne souhaitant pas en général crier leurs solutions sur les toits. Depuis la création en 1997 d’une première société diffusant un logiciel basé sur l’iconographie des corrélations, et son enseignement dans certaines universités, la bibliographie s’est largement étendue, en particulier dans les secteurs médical^[5] et astrophysique (spectrométrie de masse^[6],[7]).

Cette présentation, à visée pédagogique, s'inspire des documents cités en référence.

Qu’est-ce qu’une corrélation « remarquable » ?

Une forte corrélation n’a pas de sens isolément. Réciproquement une faible corrélation n’implique pas l’absence de lien.

Exemple 1 

Les variables A et C sont fortement corrélées parce que leurs variations sont toutes les deux liées à une variable X. En réalité il n’y a pas de lien AC, mais un lien XA et un lien XC. En d’autres termes, la corrélation entre A et C est redondante, et elle disparaît lorsque X est maintenu constant (on parle de « corrélation partielle » faible par rapport à X). D’où le schéma des seules corrélations remarquables :

Exemple 2 

La variable Y dépend de plusieurs variables C, D, E, F et G indépendantes. Aussi la corrélation de Y avec chacune d'entre elles, prise séparément, est faible (non « significative » au sens probabiliste du terme). En réalité, il existe les liens rigoureux CY, DY, EY, FY et GY. D’où le schéma des corrélations remarquables :

Sélection des liens remarquables

Illustrons-la sur un petit exemple : Lors d’un contrôle mathématique d'un niveau de classe de troisième, huit élèves de la sixième à la terminale, dont nous connaissons le poids, l'âge et l’assiduité, ont obtenu les notes suivantes :

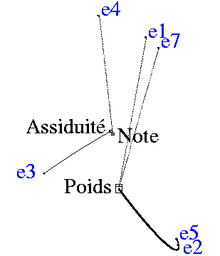
Données originelles

Élève	Poids	Âge	Assiduité	Note
e1	52	12	12	5
e2	59	12,5	9	5
e3	55	13	15	9
e4	58	14,5	5	5
e5	66	15,5	11	13,5
e6	62	16	15	18
e7	63	17	12	18
e8	69	18	9	18

Matrice de corrélation

	Poids	Âge	Assiduité	Note
Poids	1
Âge	0,885	1
Assiduité	-0,160	-0,059	1
Note	0,774	0,893	0,383	1

Plaçons les quatre variables au hasard sur le papier, et traçons un trait entre deux d’entre elles chaque fois que leur corrélation est supérieure au seuil de 0,3 en valeur absolue.

Au vu de ce schéma, la corrélation (poids,note) = 0.774, relativement forte, donne à penser que le poids a plus d’influence sur la note que l’assiduité ! Mais, d’autre part, nous avons les corrélations (poids,âge) = 0,885, et (âge,note) = 0,893.

À partir de ces 3 coefficients de « corrélation totale », la formule de la « corrélation partielle » donne : Corrélation (poids,note) à âge constant : = -0,08

La corrélation entre note et poids, à âge constant a fortement baissé (elle est même légèrement négative). En d’autres termes, le poids n’a pas d’influence sur la note. Cela n’est guère surprenant. Effaçons le lien entre poids et note :

En définitive, un lien n’est pas tracé,

• soit parce que sa corrélation totale est inférieure au seuil, en valeur absolue,
• soit parce qu’il existe au moins une corrélation partielle inférieure au seuil, en valeur absolue, ou de signe contraire à la corrélation totale.

Il n’y a pas lieu, ici, d’effacer d’autres liens, comme on le vérifie à partir des valeurs des autres corrélations partielles :

Corrélation (poids,note) à assiduité constante : = 0,92

Corrélation (âge,poids) à note constante : = 0,68

Corrélation (âge,poids) à assiduité constante : = 0,89

Corrélation (âge,note) à poids constant : = 0,71

Corrélation (assiduité,poids) à note constante : = -0,78

Corrélation (assiduité,poids) à âge constant : = -0,23

Corrélation (assiduité,note) à poids constant : = 0,81

Corrélation (assiduité,note) à âge constant : = 0,97

Corrélation (assiduité,âge) à poids constant : = 0,18

Corrélation (assiduité,âge) à note constante : = -0,97

Puisque le nombre de variables est m = 4, il y a m.(m-1)/2 = 6 couples distincts de variables et, pour chaque couple, (m-2) = 2 coefficients de corrélation partielle.

Soulignons ici une différence importante entre l’Iconographie des Corrélations et le modèle graphique gaussien :

Nous venons de voir que l’iconographie des corrélations s’appuie sur (m-2).m.(m-1)/2 = 12 coefficients de corrélations partielles, calculés, chacun, par rapport à une seule variable, donc sans mélanger les effets de chacune d’elles. Au contraire le modèle graphique gaussien repose sur les seuls m.(m-1)/2 = 6 coefficients de corrélations partielles par rapport aux (m-2) autres variables. Il agrège donc une multiplicité de relations triangulaires et en retient une sorte de moyenne (matrice de corrélation partielle de chaque couple de variable par rapport à toutes les autres variables). Il perd la mise en évidence d’une variable particulière expliquant ou infirmant la relation entre deux variables.

L’iconographie des corrélations permet donc d’augmenter à la fois la quantité et la qualité de l’information utilisée.

Instants remarquables de l’analyse

Les données disponibles permettent de pousser plus loin l’analyse.

On peut considérer en effet chaque ligne comme un « instant » de l’analyse, caractérisé par une variable indicatrice, égale à 1 à l’instant de la ligne considérée, et à 0 sinon :

Élève	Poids	Âge	Assiduité	Note	e1	e2	e3	e4	e5	e6	e7	e8
e1	52	12	12	5	1	0	0	0	0	0	0	0
e2	59	12,5	9	5	0	1	0	0	0	0	0	0
e3	55	13	15	9	0	0	1	0	0	0	0	0
e4	58	14,5	5	5	0	0	0	1	0	0	0	0
e5	66	15,5	11	13,5	0	0	0	0	1	0	0	0
e6	62	16	15	18	0	0	0	0	0	1	0	0
e7	63	17	12	18	0	0	0	0	0	0	1	0
e8	69	18	9	18	0	0	0	0	0	0	0	1

Bien que les « instants » portent les mêmes noms que les élèves, il faut se rappeler que les élèves sont des lignes (des observations), tandis que les instants sont des colonnes, qui font partie des « variables », au même titre que les 4 premières colonnes.

Nous pouvons donc adopter le même critère de tracé des liens pour les « instants » et les variables originelles. Toutefois, pour ne pas alourdir le schéma, dessinons seulement les « instants » liés à une variable au moins (« instants remarquables ») :

Les « instants » sont représentés par un triangle, pour être mieux distingués des variables originelles, qui sont représentées par un carré.

• Par rapport au schéma précédent, le lien entre note et assiduité a disparu, remplacé par les liens (Note,e6) et (Assiduité,e6) . Il était donc redondant : l’élève e6, très assidu et bien noté, explique à lui tout seul le lien (Note,Assiduité).
• L’élève e3 a une assiduité remarquablement forte, et l’élève e4 une assiduité remarquablement faible (trait pointillé).

Un lien est dit « remarquable » quand les autres liens présents sur la figure ne suffisent pas à l’expliquer.

• L’élève e6 a en effet une note « remarquable » : 18/20.
• Les élèves e7 et e8 qui ont, eux aussi, 18/20, ne sont pas remarquables : ils n’apparaissent pas sur le schéma, car, plus âgés, leur note est déjà expliquée par le lien (âge,note).

• De la même façon, on peut vérifier sur les données, que e5 a un poids remarquablement fort pour son âge (par rapport aux 8 élèves de la population étudiée) ; tandis que l’élève e1 à un poids remarquablement faible pour son âge.

Les liens entre carrés (variables-variables) soulignent les lois générales; les liens carré-triangle (variable-instant) soulignent les événements rares.

Algorithme de l’iconographie des corrélations

Si le tableau de données est petit, le principe de l’iconographie des corrélations est suffisamment simple pour permettre un tracé manuel. Sinon, il faut recourir à un programme comportant, en entrée, la matrice de corrélation et le seuil choisi (par exemple 0,3). En voici l’algorithme :

Pour éviter les redondances, le lien AB est tracé si et seulement si la corrélation totale r(A,B) est supérieure au seuil en valeur absolue, et si les corrélations partielles r(A,B), par rapport à une variable Z, sont supérieures au seuil, en valeur absolue, et de même signe que la corrélation totale, pour tout Z parmi les variables disponibles, y compris les « instants ».

Ce critère de tracé, sévère, garantit la sélection des liens les plus « solides ».

Les variables peuvent être quantitatives et/ou qualitatives (pourvu que ces dernières utilisent un codage disjonctif complet).

Position des points sur le papier

L‘exemple ci-dessus a montré deux sortes de points : les variables (carrés), et les « instants » (triangles). Une fois trouvé les liens entre ces éléments, positifs (traits pleins) ou négatifs (traits pointillé), il reste à les dessiner sur le papier.

Toute latitude de positionnement est laissée à l’analyste, puisque l’interprétation dépend des liens et non des positions.

Autant que possible, il faut éviter les croisements inutiles entre liens, gênant la lecture. Le schéma suivant, par exemple, est moins lisible que le précédent, bien que l’interprétation soit la même (liens identiques) :

Plusieurs approches peuvent être utilisées pour disposer les points de façon automatique.

Une première approche consiste à projeter le nuage de points des variables sur les deux premiers axes d’une analyse en composantes principales. Mais les projections ne sont pas toujours adaptées à une bonne lisibilité lorsqu’il y a beaucoup de composantes principales statistiquement significatives, et particulièrement en cas de mélange de variables qualitatives et quantitatives.

Une deuxième approche repose sur les algorithmes de force (Kamada-Kawai ou Fruchterman et Reingold par exemple) qui simulent un système de ressorts sur les arêtes du graphe : la définition d'une force répulsive entre les arêtes, et d'une force attractive ente les arêtes connectées permet d'obtenir un équilibre. Le dessin est en général satisfaisant pour les structures arborescentes, mais, au-delà de quelques dizaines de sommets, la compréhension est difficile en cas de structures bouclées sur plusieurs dimensions.

Enfin, une troisième approche consiste à tirer parti de l’interprétation géométrique du coefficient de corrélation (cosinus), et à dessiner le schéma à la surface d’une sphère à 3 dimensions :

• L'arc-cosinus de la corrélation étant une distance angulaire, deux points seront d’autant plus proches sur la sphère qu’ils seront plus corrélés (positivement). Inversement, la distance angulaire entre deux points corrélés négativement est un angle obtus ; si la corrélation vaut -1, les points sont opposés sur la sphère (angle 180°).
  Il s’agit d’un pis aller, car la sphère réelle n’est pas à 3 dimensions, mais à n dimensions. Si donc deux points très corrélés sont forcément proches sur le dessin, l’inverse n’est pas sûr : deux points très proches sur le dessin ne sont pas forcément corrélés. Toutefois, l’absence de lien tracé lève l’ambiguïté.
• On pourrait envisager bien d’autres modes de choix des positions : le plus utilisé consiste à choisir comme distance angulaire l’arc-cosinus de la valeur absolue de la corrélation. Ainsi les points corrélés négativement ne sont pas opposés sur la sphère, et le lien pointillé est plus court et encombre moins le schéma.
  En pratique, dans une approche logicielle, une première variable A est dessinée n'importe où sur la sphère. Puis la variable B la moins corrélée à cette première est posée sur la sphère à la distance arc-cosinus(r(A,B)) de la première. On place alors, par triangulation, la variable C la moins corrélée aux deux premières. Les autres points sont posés de proche en proche. Si la quatrième variable a une corrélation nulle avec les trois premières, il n'est matériellement pas possible de lui assigner une position exacte. Les distances sont recalculées de façon proportionnelle aux valeurs réelles. Au bout d'un certain temps, la position des premiers points est recalculée d'après les suivants. Etc. Ainsi, la figure est réajustée progressivement.
• L’algorithme, qui s’ajuste autant que possible aux distances réelles, n’est donc pas bloqué si la structure se déploie dans plus de trois dimensions. Et, même si elle contient plusieurs milliers de variables, il est toujours possible d’en prendre un extrait qui peut s’étaler à la surface de la sphère pour sauvegarder la lisibilité. Etant déterministes, puisque les positions sur la sphère à n dimensions sont connues avec certitude, les calculs sont rapides.

Choix du seuil

Le seuil peut varier entre 0 et 1. Un lien n'est tracé que si, non seulement la corrélation totale, mais encore toutes les corrélations partielles correspondantes, sont supérieures au seuil en valeur absolue, et de même signe. Cette condition est sévère, et les liens qui subsistent sont, en général, riches d’information.

Augmenter la valeur du seuil diminue le nombre de liens, et clarifie la figure, mais diminue aussi l’information, surtout quand la variable d’intérêt dépend de plusieurs variables indépendantes.

Il est souvent préférable de prendre un seuil assez bas. Puis, si la figure complète est trop touffue, de ne dessiner que les liens à la variable d’intérêt.

À titre d’exemple, lorsqu’on aborde de nouvelles données, et qu’on ne sait pas quel seuil choisir, on pourra commencer par :

• un seuil = 0.3 pour une analyse de données ;
• un seuil = 0.1 pour l’analyse des résultats d’un plan d’expériences. Dans ce cas en effet, tous les facteurs sont contrôlés, et l’on peut se permettre de ne pas dessiner les « instants » (a priori remarquables par construction du plan), ce qui allège la figure ;
• un seuil = 0.01, ou moins, pourra même être choisi lorsque le tableau de données comprend plusieurs centaines d’observations.

Dans notre exemple, même au seuil nul, le lien (poids,note) n’est pas tracé, car la corrélation partielle par rapport à l’âge est de signe contraire à la corrélation totale. Mais le lien (assiduité,note) apparaît, et il y a plus d’instants remarquables.

Organisation des liens

L’iconographie des corrélations vise à mettre en évidence l’organisation des liens, qui peut aussi bien être bouclée que hiérarchique ou continûment répartie.

L’absence d’axe, quelle que soit la dimension du problème permet de remplacer une multitude de projections bidimensionnelles par une image unique, où l’essentiel apparaît d’un coup d’œil.

Une succession de telles figures (éventuellement sous forme de dessin animé) autorise la représentation graphique d’une organisation multidimensionnelle évolutive.

Retrait d’une influence évidente

Il est courant, en analyse de données, de disposer d’une variable Z dont l’influence, prépondérante et déjà bien connue, masque des phénomènes plus fins que l’on cherche à découvrir.

La solution consiste à tracer le schéma, non pas de la matrice de corrélation totale, mais de la matrice des corrélations partielles par rapport à Z, afin de retirer toute influence linéaire de Z sur les autres variables. Le schéma révèle alors une autre organisation, abstraction faite des variations de Z.

Par exemple, retirons la composante de l’âge, dont l’influence, prépondérante, est bien connue. Le schéma révèle alors l’influence directe de l’assiduité sur la note. L’âge a disparu de la figure, ainsi que sa composante dans toutes les variables. Et le poids se trouve isolé.

Dans un tableau de données comportant plus de variables, il peut être intéressant de retirer plusieurs influences (le résultat ne dépend pas de l’ordre dans lequel elles sont retirés).

Interactions logiques remarquables

De même que les « instants » sont rajoutés, ci-dessus, au tableau initial, comme de nouvelles colonnes, de même on peut rajouter d’autres colonnes, par exemple des fonctions des variables initiales, en particulier des « interactions logiques », qui sont des couplages de variables.

Le nombre de colonnes supplémentaires importe peu, pourvu qu’on ne rajoute sur le schéma que celles qui seront liées à l’une au moins des variables initiales, afin de ne pas alourdir inutilement la figure.

Par exemple, suite à l’ajout de nouvelles colonnes correspondant au « & » logique entre deux variables quelconques, seule l’interaction « Age&Assiduité » apparaît directement liée à la note :

L’interaction logique apporte quelque chose de plus à l’interprétation (compte tenu du petit nombre de variables explicatives disponibles dans cet exemple) : pour obtenir une bonne note il ne suffit pas d’être plus âgé, il faut aussi être assidu au cours.

Base de connaissance associée au schéma

Les liens du schéma peuvent être décrits de la manière suivante : à chaque lien tracé, associons une règle du type SI…ALORS …, suivie de la valeur du coefficient de corrélation totale, précédé d’une « * » si le lien est tracé, et de « ? » si le lien n’est pas tracé, car « douteux » (la valeur de la corrélation n’est supérieure au seuil qu’à cause d’une seule observation).

SI Poids ALORS Age *.885

SI Age ALORS Poids *.885

SI Age ALORS Note *.893

SI Note ALORS Age *.893

SI Assiduité ALORS Age&Assiduité ?.493

SI Note ALORS Age&Assiduité *.960

SI Age&Assiduité ALORS Note *.960

SI .e1 ALORS Poids *-.610

SI .e3 ALORS Assiduité *.484

SI .e4 ALORS Assiduité *-.726

SI .e5 ALORS Poids *.395

SI .e6 ALORS Age&Assiduité *.597

Les liens entre variables sont indiqués ici dans les deux sens, car la causalité n’est pas directement déductible de la corrélation. Les liens « instants remarquables » - variables peuvent être indiqués dans un seul sens, car la variable découle de sa réalisation à l’instant considéré.

Une base de connaissance peut servir d’entrée à un système expert et l’utilisateur peut l’enrichir ou la préciser. Par exemple, il est contraire au bon sens de dire qu’une bonne note peut causer l’âge. C’est l’inverse qui est possible. De même, les enfants prennent du poids en grandissant, mais ce n’est pas le poids qui fait le nombre des années. L’utilisateur peut donc supprimer les règles « SI Note ALORS Age *.893 », «  SI Note ALORS Age&Assiduité *.960 » et « SI Poids ALORS Age *.885 ».

La base de connaissance ainsi modifiée donne un schéma où certains liens sont désormais orientés. On peut lui appliquer la théorie des graphes et en tirer des flux d’informations.

Champs d’application de l’iconographie des corrélations

Un moyen de ne rien oublier d’essentiel dans un tableau de donnée

Le tableau suivant est difficile à appréhender d’un coup d’œil :

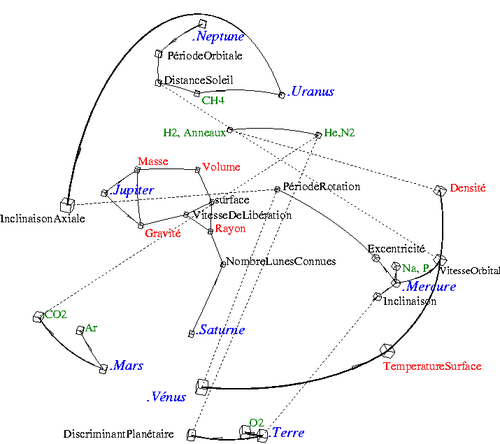
	Mercure	Vénus	Terre	Mars	Jupiter	Saturne	Uranus	Neptune
DistanceSoleil	0.387099	0.723332	1	1.523662	5.203363	9.53707	19.19126	30.06896
Rayon	0.3825	0.9488	1	0.53226	11.209	9.449	4.007	3.883
Surface	0.1471	0.901	1	0.2745	125.5	86.27	15.88	15.1
Volume	0.056	0.87	1	0.151	1321.3	763.59	63.086	57.74
Masse	0.055	0.815	1	0.107	318	95	14	17
Densité	5.43	5.24	5.515	3.94	1.33	0.697	1.29	1.76
Gravité	3.7	8.87	9.81	3.71	23.12	8.96	8.69	11
VitesseDeLibération	4.25	10.36	11.18	5.02	59.54	35.49	21.29	23.71
PériodeRotation	58.64622	-243.018	0.997269	1.025957	0.41354	0.44401	-0.7183	0.67125
PériodeOrbitale	0.240847	0.615197	1.000017	1.880848	11.86261	29.4475	84.01685	164.7913
VitesseOrbitale	47.8725	35.0214	29.7859	24.1309	13.0697	9.6724	6.8352	5.4778
Excentricité	0.205631	0.006773	0.016710	0.093412	0.048392	0.054150	0.047167	0.008585
Inclinaison	7.00487	3.39471	0.00005	1.85061	1.3053	2.48446	0.76986	1.76917
InclinaisonAxiale	0	177.3	23.45	25.19	3.12	26.73	97.86	29.58
TempératureSurface	166.85	456.85	17.35	-46	-121.15	-139.15	-197.15	-220.15
He	1	0	0	0	1	1	1	1
Na	1	0	0	0	0	0	0	0
P	1	0	0	0	0	0	0	0
CO2	0	1	0	1	0	0	0	0
N2	0	1	1	1	0	0	0	0
O2	0	0	1	0	0	0	0	0
Ar	0	0	0	1	0	0	0	0
H2	0	0	0	0	1	1	1	1
CH4	0	0	0	0	0	0	1	1
NombreLunesConnues	0	0	1	2	63	60	27	13
Anneaux	0	0	0	0	1	1	1	1
DiscriminantPlanétaire	9.1	135	170	18	62.5	19	2.9	2.4

Liens entre les variables (iconographie des corrélations)

Traits plein : corrélations positives Traits pointillés : corrélations négatives

La figure montre les liens plus ou moins évidents (comme celui de la gravité avec la vitesse de libération) ; et aussi les liens propres à chaque planète.

C’est un moyen de ne rien oublier d’important.

Par exemple, les liens de la figure s'interprètent comme suit:

• Les planètes à forte vitesse orbitale (comme Mercure) ont aussi une forte densité et une forte température (en particulier Vénus).
• La Terre a une faible inclinaison (trait pointillé), beaucoup d’O₂ dans son atmosphère, et un fort discriminant planétaire (traits pleins).
• Une plus grande période de rotation correspond à une faible inclinaison axiale et à une forte excentricité.
• Etc.

On pourrait augmenter le nombre de liens remarquables en baissant le seuil du tracé. Il faudrait alors, pour garder un dessin lisible, n'en dessiner qu'une partie: par exemple les liens à une variable d'intérêt.

L’analyse des grands tableaux de bord

Le tableau de bord de gestion est un moyen d’analyse et de diagnostic. Constitué de plusieurs indicateurs de performance, il permet de connaître la charge de travail, d’apercevoir l’hypertrophie ou l’atrophie d’exécution des différentes tâches, de situer les anomalies de fonctionnement, de redresser certaines situations. Cependant, compte tenu des limites de notre mémoire, un tableau de bord doit comporter peu de chiffres pour être d’emploi facile.

L’iconographie des corrélations est un moyen d’analyser un tableau de bord qui a beaucoup de chiffres, et d’exploiter vraiment toutes les informations de l’entreprise. Pouvant s’affranchir des influences extérieures (telles que tendances économiques ou décisions de marketing), elle permet de mieux mettre en évidence l’influence mutuelle des tâches, d’analyser les causes d’écart entre prévision et réalisation, et, grâce au schéma synthétique, de faire remonter rapidement l’information brute sous forme de préconisations opérationnelles.

Une alternative à la stratification

La stratification consiste à découper la base de données en groupes homogènes (strates). Dans l’exemple examiné plus haut, la stratification consisterait à faire des groupes d’élèves de même âge, et des sous-groupes d’élèves de même assiduité. Cela permettrait de s’affranchir, dans chaque groupe de l’effet de l’âge, et dans chaque sous-groupe de l’effet de l’assiduité. Malheureusement tous nos élèves ont un âge différent !

En fait, stratifier n’est intéressant que si la variable de stratification est corrélée au paramètre d’intérêt. De plus, les strates ne doivent pas être vides. Il n’est donc pas possible de stratifier sur beaucoup de variables ou sur une faible population.

L’iconographie des corrélations, au contraire, permet de s’affranchir de l’effet de l’âge même si la stratification est impossible, pourvu que l’âge soit connu.

C’est pourquoi, en iconographie des corrélations, un grand nombre de variables en rapport avec le problème ne complique pas l’analyse. Au contraire, il ne peut qu’affiner la représentation. Il est donc recommandé de commencer d’emblée l’analyse sur toutes les variables disponibles : c’est le moyen de s’affranchir le plus tôt possible des « fausses bonnes corrélations » qui peuvent nous engager sur de fausses pistes (biais, facteurs de confusions).

Voir aussi

• Le Réseau bayésien est un graphe dans lequel les relations de cause à effet sont probabilisées, au contraire de l’Iconographie des corrélations, dont le principe est géométrique.

Références

• Portail des probabilités et des statistiques