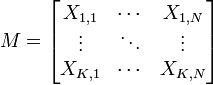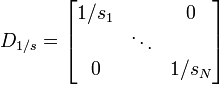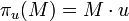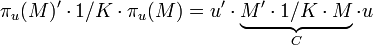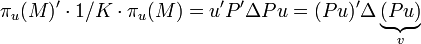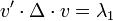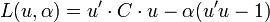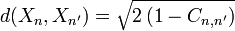- Transformée de Karhunen-Loève
-
Analyse en composantes principales
 Pour les articles homonymes, voir ACP.
Pour les articles homonymes, voir ACP.L'Analyse en Composantes Principales (ACP) est une Analyse Factorielle de la famille de l'Analyse des données et de la Statistique Multivariée, qui consiste à transformer des variables liées entre elles (dites "corrélées" en statistique) en nouvelles variables indépendantes les unes des autres (donc "non corrélées"). Ces nouvelles variables sont nommées "composantes principales", ou axes. Elle permet au praticien de réduire l'information en un nombre de composantes plus limité que le nombre initial de variables.
Il s'agit d'une approche à la fois géométrique (représentation des variables dans un nouvel espace géométrique selon des directions d'inertie maximale) et statistique (recherche d'axes indépendants expliquant au mieux la variabilité - la variance - des données). Lorsqu'on veut alors compresser un ensemble de N variables aléatoires, les n premiers axes de l'ACP sont un meilleur choix, du point de vue de l'inertie ou la variance expliquée (cf plus loin).
Sommaire
Histoire
L'ACP prend sa source dans un article de Karl Pearson publié en 1901[1]. Le père du Test du χ² y prolonge ses travaux dans le domaine de la régression et des corrélations entre plusieurs variables. Pearson utilise ces corrélations non plus pour expliquer une variable à partir des autres (comme en régression), mais pour décrire et résumer l'information contenue dans ces variables.
Encore connue sous le nom de transformée de Karhunen-Loève ou de transformée de Hotelling, l'ACP a été de nouveau développée et formalisée dans les années 30 par Harold Hotelling[2] . La puissance mathématique de l'économiste et statisticien américain le conduira aussi à développer l'analyse canonique, généralisation des analyses factorielles dont fait partie l'ACP.
Les champs d'application sont aujourd'hui multiples, allant de la biologie à la recherche économique et sociale, et plus récemment le traitement d'images. L'ACP est majoritairement utilisée pour:
- décrire et visualiser des données ;
- les décorréler ; dans la nouvelle base, constituée des nouveaux axes, les variables ont une corrélation nulle ;
- les débruiter, en considérant que les axes que l'on décide d'oublier sont des axes bruités.
Exemples pour comprendre
Premier Exemple:
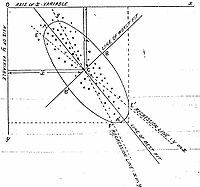
Dans le cas d'une image, comme dans la figure ci-contre, les pixels sont représentés dans un plan et considérés comme une variable aléatoire à deux dimensions. L'ACP va déterminer les deux axes qui expliquent le mieux la dispersion de l'objet, interprété comme un nuage de points. Elle va aussi les ordonner par inertie expliquée, le second axe étant perpendiculaire au premier.
Second exemple:Dans une école imaginaire, on n'enseigne que deux matières sur lesquelles les élèves sont notés: le français et les mathématiques. En appliquant l'ACP au tableau de notes, on dégagera probablement en premier axe des valeurs par élève très proches de leur moyenne générale dans les deux matières. C'est cet axe qui résumera aux mieux la variabilité des résultats selon les élèves. Mais un bon professeur s'intéressa aussi au second axe, indépendant du premier, qui mettra probablement en évidence les élèves d'un profil plus littéraire et ceux d'un profil plus scientifique (écart entre la note en français et la note en mathématiques).
On comprend l'intérêt de la méthode d'ACP quand on étend l'analyse à 10 matières enseignées: la méthode va calculer pour chaque élève 10 nouvelles valeurs, selon 10 axes, chacun étant indépendant des autres. Les derniers axes apporteront très peu d'information au plan statistique: ils mettront probablement en évidence quelques élèves au profil singulier. Selon son point de vue d'analyse, notre bon professeur veillera à ces élèves dans sa pratique quotidienne, corrigera peut-être une erreur qui s'est glissée dans son tableau, mais ne prendra pas en compte les derniers axes s'il s'agit d'une réflexion pédagogique plus globale.
La puissance de l'ACP est qu'elle sait aussi prendre en compte des données de nature hétérogène: par exemple un tableau des différents pays du monde avec le PNB par habitant, le taux d'alphabétisation, le taux d'équipement en téléphones portables, le prix du moyen du hamburger, etc...Elle permet d'avoir une intuition rapide des effets conjoints entre ces variables.
Échantillon
On applique usuellement une ACP sur un ensemble de N variables aléatoires X1, …, XN connues à partir d'un échantillon de K réalisations conjointes de ces variables.
Cet échantillon de ces N variables aléatoires peut être structuré dans une matrice M à K lignes et N colonnes.
Chaque variable aléatoire Xn = (X1, n, …, XK, n)' a une moyenne
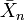 et un écart type σXn.
et un écart type σXn.Poids
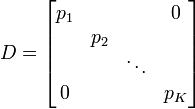
Si les réalisations (les éléments de la matrice M) sont à probabilités égales alors chaque réalisation (un élément Xi,j de la matrice) a la même importance 1 / n dans le calcul des caractéristiques de l'échantillon. On peut aussi appliquer un poids pi différent à chaque réalisation conjointes des variables (cas des échantillons redressés, des données regroupées, ...). Ces poids, qui sont des nombres positifs de somme 1 sont représentés par une matrice diagonale D de taille K:
Dans le cas le plus usuel de poids égaux,
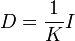 où I est la matrice identité.
où I est la matrice identité.Transformations de l'échantillon
Le vecteur
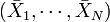 est le centre de gravité du nuage de points ; on le note souvent g. On a g = M'D1 où 1 désigne le vecteur de Rn dont toutes les composantes sont égales à 1.
est le centre de gravité du nuage de points ; on le note souvent g. On a g = M'D1 où 1 désigne le vecteur de Rn dont toutes les composantes sont égales à 1.La matrice M est généralement centrée sur le centre de gravité :
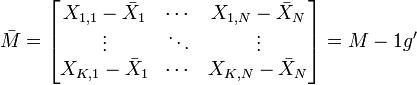 .
.
Elle peut être aussi réduite :
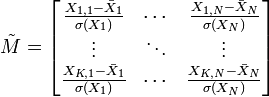 .
.
Le choix de réduire ou non le nuage de points (i.e. les K réalisations de la variable aléatoire (X1, …, XN)) est un choix de modèle :
- si on ne réduit pas le nuage : une variable à forte variance va « tirer » tout l'effet de l'ACP à elle ;
- si on réduit le nuage : une variable qui n'est qu'un bruit va se retrouver avec une variance apparente égale à une variable informative.
Calcul de covariances et de corrélations
Une fois la matrice M transformée en
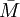 ou
ou 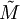 , il suffit de la multiplier par sa transposée pour obtenir:
, il suffit de la multiplier par sa transposée pour obtenir:- la matrice de variance-covariance des X1, …, XN si M n'est pas réduite ;
- la matrice de corrélation des X1, …, XN si M est réduite.
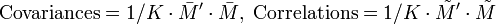
Ces deux matrices sont carrées (de taille N), symétriques, et réelles. Elles sont donc diagonalisables dans une base orthonormée.
De façon plus générale, la matrice de variance-covariance s'écrit
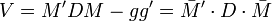 . Si l'on note D1 / s la matrice diagonale des inverses des écarts-types:
. Si l'on note D1 / s la matrice diagonale des inverses des écarts-types:et
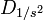 la matrice diagonale des inverses des variances, alors on a:
la matrice diagonale des inverses des variances, alors on a: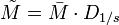 .
.
La matrice des coefficients de corrélation linéaire entre les N variables prises deux à deux, notée R, s'écrit:
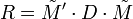 .
.
Critère d'inertie
Dans la suite de cet article, nous considèrerons que le nuage est transformé (centré et réduit si besoin est). Chaque Xn est donc remplacé par
 ou
ou  . Nous utiliserons donc la matrice M pour noter
. Nous utiliserons donc la matrice M pour noter 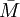 ou
ou 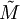 suivant le cas.
suivant le cas.Le principe de l'ACP est de trouver un axe u, issu d'une combinaison linéaire des Xn, tel que la variance du nuage autour de cet axe soit maximale.
Pour bien comprendre, imaginons que la variance de u soit égale à la variance du nuage; on aurait alors trouvé une combinaison des Xn qui contient toute la diversité du nuage original (en tout cas toute la part de sa diversité captée par la variance).
Comme le titre de cette section l'indique, le critère couramment utilisé est la variance de l'échantillon (on veut maximiser la variance expliquée par le vecteur u). Pour les physiciens, cela a plutôt le sens de maximiser l'inertie expliquée par u (c'est-à-dire minimiser l'inertie du nuage autour de u).
Projection
Finalement, nous cherchons le vecteur u tel que la projection du nuage sur u ait une variance maximale. La projection de l'échantillon des X sur u s'écrit :
la variance empirique de πu(M) vaut donc :
où C est la matrice de covariance.
Comme nous avons vu plus haut que C est diagonalisable dans une base orthonormée, notons P le changement de base associé et Δ la matrice diagonale formée de son spectre :
Après cette réécriture, nous cherchons le vecteur unitaire v qui maximise v'Δv, où Δ = Diag(λ1, …, λN) est diagonale (rangeons les valeurs de la diagonale de Δ en ordre décroissant). On peut rapidement vérifier qu'il suffit de prendre le premier vecteur unitaire ; on a alors :
Plus formellement, on démontre ce résultat en maximisant la variance empirique des données projetées sur u sous la contrainte que u soit de norme 1 (par un Multiplicateur de Lagrange α) :
On obtient ainsi les deux résultats suivants:
- u est vecteur propre de C associé à la valeur propre λ1
- u est de norme 1
La valeur propre λ1 est la variance empirique sur le premier axe de l'ACP.
On continue la recherche du deuxième axe de projection w sur le même principe en imposant qu'il soit orthogonal à u
Diagonalisation
La diagonalisation de la matrice de corrélation (ou de covariance si on se place dans un modèle non réduit), nous a permis d'écrire que le vecteur qui explique le plus d'inertie du nuage est le premier vecteur propre. De même le deuxième vecteur qui explique la plus grande part de l'inertie restante est le deuxième vecteur propre, etc.
Nous avons vu en outre que la variance expliquée par le k-ième vecteur propre vaut λk.
Finalement, la question de l'ACP se ramène à un problème de diagonalisation de la matrice de corrélation
Numériquement
Numériquement, la matrice M étant rectangulaire, il est plus économique de la décomposer en valeurs singulières, puis de recombiner la décomposition obtenue, plutôt que de diagonaliser M' M.
Résultats théoriques
Si les sections précédentes ont travaillé sur un échantillon issu de la loi conjointe suivie par X1, …, XN, que dire de la validité de nos conclusions sur n'importe quel autre échantillon issu de la même loi ?
Plusieurs résultats théoriques permettent de répondre au moins partiellement à cette question, essentiellement en se positionnant par rapport à une distribution gaussienne comme référence.
Applications
L'Analyse en Composantes Principales est usuellement utilisée comme outil de compression linéaire. Le principe est alors de ne retenir que les n premiers vecteurs propres issus de le diagonalisation de la matrice de corrélation (ou covariance), lorsque l'inertie du nuage projeté sur ces n vecteurs représente qn pourcents de l'inertie du nuage original, on dit qu'on a un taux de compression de 1 - qn pourcents, ou que l'on a compressé à qn pourcents. Un taux de compression usuel est de 20 %.
Les autres méthodes de compressions statistiques habituelles sont:
- l'analyse en composantes indépendantes ;
- les cartes auto-adaptatives (SOM, self organizing maps en anglais) ; appelées aussi cartes de Kohonen ;
- l'Analyse en composantes curvilignes ;
- la compression par ondelettes.
Il est possible d'utiliser le résultat d'une ACP pour construire une classification statistique des variables aléatoires X1, …, XN, en utilisant la distance suivante (Cn, n' est la corrélation entre Xn et Xn' ):
Notes
- ↑ (en) Pearson, K., « On Lines and Planes of Closest Fit to Systems of Points in Space », dans Philosophical Magazine, vol. 2, no 6, 1901, p. 559–572 [[pdf] texte intégral]
- ↑ Analysis of a Complex of Statistical Variables with Principal Components",1933, Journal of Educational Psychology
Voir aussi
- Valeurs propres
- Compression statistique
- Équilibre biais / variance
- Analyse de la variance
- Partitionnement de données
- Iconographie des corrélations
Références
- Jean-Paul Benzécri ; Analyse des données. T2 (leçons sur l'analyse factorielle et la reconnaissance des formes et travaux du Laboratoire de statistique de l'Université de Paris 6. T. 2 : l'analyse des correspondances), Dunod Paris Bruxelles Montréal, 1973
- Jean-Paul Benzécri et Al. Pratique de l'analyse des données. T1 (analyse des correspondances. Exposé élémentaire), Dunod Paris, 1984,
- Jean-Paul Benzécri et Al. Pratique de l'analyse des données. T2 (abrégé théorique. Études de cas modèle), Dunod Paris, 1984
- Escofier Brigitte, Pagès Jérôme ; Analyse factorielles simples et multiples. Objectifs, méthodes et interprétation, Dunod Paris, 1988
- Lebart Ludovic, Morineau Alain, Piron Marie; Statistique exploratoire multidimensionnelle, Dunod Paris, 1995
- Michel Volle, Analyse des données, Economica, 4e édition, 1997, ISBN 2717832122
- Portail des probabilités et des statistiques
Catégorie : Analyse des données
Wikimedia Foundation. 2010.