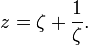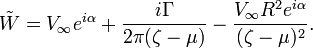Transformée de Joukovsy

Transformée de Joukovsy

Transformation de Joukovsky

"Profil de Joukowky"
Exemple d'une transformée de Joukowsky. Le cercle de dessus est transformé en profil de Joukowsky dessous

La transformation de Joukovsky, du nom du savant aérodynamicien russe Nikolaï Joukovski, est une transformation conforme utilisée historiquement dans le calcul des profils d'aile d'avion.

Sommaire

Définition

La transformée s'écrit :

z=\zeta+\frac{1}{\zeta}.\,

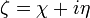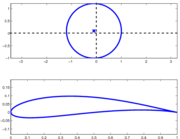
Où z=x+iy\, est un nombre complexe et \zeta=\chi + i \eta \, est une variable complexe.

Le profil de Joukovsky est engendré dans un plan 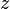z\, par l'application de la transformée à un cercle du plan 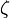\zeta\, qui passe par le point d'affixe (0,1). Les coordonnées du centre du cercle sont les variables dont dépend la forme du profil.

L'écoulement autour d'un cercle est décrit par des équations particulièrement simples. En appliquant la transformation de Joukovsky, on trouve l'écoulement autour du profil considéré.

La vitesse complexe 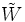\tilde{W} autour du cercle dans le plan \zeta\, est

\tilde{W}=V_\infty e^{i \alpha} + \frac{i \Gamma}{2 \pi (\zeta -\mu)} - \frac{V_\infty R^2 e^{i \alpha}}{(\zeta-\mu)^2}.

où

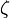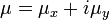  • \mu=\mu_x+i \mu_y\, est la coordonnée complexe du centre du cercle
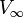  • V_\infty\, est la vitesse du fluide en dehors de toute perturbation
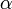  • \alpha\, est l'angle d'incidence du profil par rapport à l'écoulement
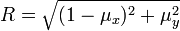
  • R est le rayon du cercle, calculé avec R=\sqrt{(1-\mu_x)^2+\mu_y^2}\,
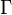  • \Gamma\, est la circulation qui définit la portance selon le théorème de Kutta-Jukowski. La condition de Kutta permet de calculer cette circulation :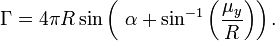 \Gamma=4\pi R \sin \left(\ \alpha + \sin^{-1} \left( \frac{\mu_y}{R} \right)\right).

Application

À partir de cette vitesse, d'autres propriétés de l'écoulement, comme les coefficients de pression et de portance du profil peuvent être calculées. Cependant, cette méthode ne permet pas de calculer le coefficient de traînée (les hypothèses à la base du calcul, fluide parfait et écoulement bidimensionnel, conduisent à une traînée nulle).

Les aéronefs équipés de profils de Joukovsky avaient besoin d'importantes motorisations ; ils ne furent plus guère utilisés après la Première Guerre mondiale.

Transformation de Karman-Trefftz

Un profil de Joukovsky possède un point de rebroussement au bord de fuite . La transformation de Karman-Trefftz engendre des profils à bord de fuite d'angle non nul, plus réalistes au point de vue mécanique. Elle requiert un paramètre supplémentaire, l'angle du bord de fuite.

Voir aussi

Références

  • (en) John Anderson, Fundamentals of Aerodynamics, McGraw-Hill, Toronto, 1991 (ISBN 0-07-001679-8), p. 195–208 
  • D.W. Zingg, "Low Mach number Euler computations", 1989, NASA TM-102205

Liens externes

  • Portail des mathématiques Portail des mathématiques
  • Portail de l’aéronautique Portail de l’aéronautique
Ce document provient de « Transformation de Joukovsky ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformée de Joukovsy de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Transformée de joukovsy — Transformation de Joukovsky Exemple d une transformée de Joukowsky. Le cercle de dessus est transformé en profil de Joukowsky dessous La transformation de Joukovsky, du nom du savant aérodynamicien russe Nikolaï Joukovski, est une transformation… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”