Transformation de legendre

Transformation de legendre

Transformation de Legendre

La transformation de Legendre est une opération mathématique qui, schématiquement, transforme une fonction définie par sa valeur en un point en une fonction définie par sa tangente.

Les cas classiques d'utilisation de la transformation de Legendre se rencontrent en thermodynamique et en mécanique lagrangienne. En thermodynamique, elle permet de calculer le potentiel thermodynamique adapté à des conditions particulières. En mécanique, elle permet de passer du lagrangien au hamiltonien.

Sommaire

Principe

Soit une fonction d'état E des variables B,D,...,G dont la différentielle s'écrit par exemple dans le voisinage d'un état défini par B = B0,D = D0,...,G = G0 :

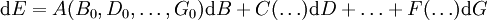
\mathrm dE = A(B_0,D_0, \ldots,G_0)\mathrm dB + C(\ldots) \mathrm dD + \ldots + F(\ldots)\mathrm dG ~

que l'on écrit formellement :

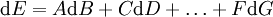
\mathrm dE = A \mathrm dB + C \mathrm dD + \ldots + F \mathrm dG ~

Si F est non nulle autour du point considéré B = B0,D = D0,...,G = G0 , alors pour B,D,... fixés la restriction de la fonction E à la variable G est localement bijective autour de G = G0 pour B = B0,D = D0,.... On peut alors créer une nouvelle fonction d'état E' dépendant cette fois du jeu de variables (B,D...,F) possédant un extremum pour B,D,... fixés autour de F = F(B0,D0,G0) en considérant les variables conjuguées F et G et en posant :

E' = E - FG ~

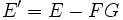
(Si on avait eu dE = AdB + CdD + ... − FdG on aurait posé E' = E + FG)

La différentielle de E' sera alors :

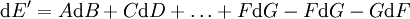
\mathrm dE' = A\mathrm dB + C\mathrm dD + \ldots + F\mathrm dG - F\mathrm dG - G\mathrm dF ~

Qui se simplifie sous la forme :

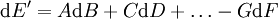
\mathrm dE' = A\mathrm dB + C\mathrm dD + \ldots - G\mathrm dF ~

Et nous voyons que la nouvelle fonction d'état E' possède le même nombre de variables indépendantes que la fonction d'état E. La différence réside dans le fait que E se basait sur la variable G alors que E' se base sur la variable F.

Ceci sera particulièrement utile dans le cas ou on dispose des moyens matériels d'imposer au système depuis l'extérieur la valeur de F, qui n'est pas une variable naturelle du système. On crée donc une fonction d'état dans laquelle F devient une variable du système, que l'on peut alors fixer ; Par exemple en thermodynamique, le récipient rigide impose le volume du gaz contenu indépendamment de sa pression (si le récipient est suffisamment solide !). Nous voyons aux lignes suivantes que l'on crée à partir de la fonction d'état « énergie interne » une fonction d'état « enthalpie » qui prend en charge ce problème. Au contraire , dans le cas ou le récipient n'est pas une bouteille mais par exemple un ballon dégonflé, ce n'est plus le volume qui est imposé de l'extérieur mais bien la pression. La fonction d'état énergie interne est donc adaptée pour traiter ce problème.

Au total, la transformation de Legendre permet en fait de modifier l'ensemble des variables indépendantes pour avoir un ensemble de variables mieux adaptées au problème considéré.

Exemple des fonctions thermodynamiques

Considérons, à titre d'exemple, l'énergie interne d'un système dont l'une des principales différentielles peut s'écrire :

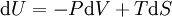
\mathrm dU = -P\mathrm dV + T\mathrm dS ~

Qui serait bien adapté à un contexte ou l'on maîtrise bien le volume V et l'entropie S en tant que variables indépendantes

  • Compte tenu de la présence du terme − PdV, nous pouvons faire une transformation de Legendre en ajoutant PV à la fonction d'état U.
  • Compte tenu de la présence du terme TdS, nous pouvons faire une transformation de Legendre en enlevant TS à la fonction d'état U.

En ajoutant PV

Si l'on ajoute PV, on obtient une nouvelle fonction d'état H que l'on appelle enthalpie.

H = U + PV ~

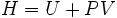
Sa différentielle est alors :

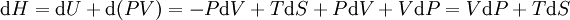
\mathrm dH = \mathrm dU + \mathrm d(PV) = -P\mathrm dV + T\mathrm dS + P\mathrm dV + V\mathrm dP = V\mathrm dP + T\mathrm dS ~

Et nous voyons que l'on a obtenu une fonction d'état H bien adapté à un contexte ou l'on maîtrise la pression P et l'entropie S en tant que variables indépendantes.

En retranchant TS

Si l'on retranche TS, on obtient une nouvelle fonction d'état F que l'on appelle énergie libre.

F = U - TS ~

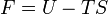
Sa différentielle est alors :

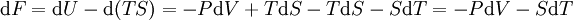
\mathrm dF = \mathrm dU - \mathrm d(TS) = -P\mathrm dV + T\mathrm dS - T\mathrm dS - S\mathrm dT = -P\mathrm dV - S\mathrm dT ~

Et nous voyons que l'on a obtenu une fonction d'état F bien adaptéE à un contexte ou l'on maîtrise le volume V et la température T en tant que variables indépendantes comme les réactions chimiques à volume constant et à température constante. C'est le cas si l'on provoque une réaction chimique entre plusieurs gaz dans une bombe calorimétrique avec des produits gazeux et si l'on ramène la température des produits à la température qu'avaient les réactifs avant la réaction.

En ajoutant PV et en retranchant TS

On peut, bien sur, faire les deux opérations simultanément. Cette transformation de Legendre nous permet d'obtenir une autre fonction d'état G que l'on appelle enthalpie libre.

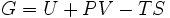
G = U + PV - TS ~

Sa différentielle est alors :

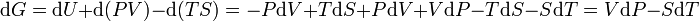
\mathrm dG = \mathrm dU + \mathrm d(PV) - \mathrm d(TS) = -P\mathrm dV + T\mathrm dS + P\mathrm dV + V\mathrm dP - T\mathrm dS - S\mathrm dT = V\mathrm dP - S\mathrm dT ~

Et nous voyons que l'on a obtenu une fonction d'état G bien adaptée à un contexte ou l'on maîtrise la pression P et la température T en tant que variables indépendantes comme les réactions chimiques à pression constante et à température constante. C'est le cas si l'on provoque une réaction chimique à l'air libre, c'est-à-dire soumise à la pression atmosphérique et si l'on ramène la température des produits à la température qu'avaient les réactifs avant la réaction.

Le cas du potentiel chimique

La différentielle exacte de l'énergie interne dans ses variables naturelles est :

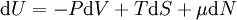
\mathrm dU = -P\mathrm dV + T\mathrm dS +\mu \mathrm dN ~

ou N est le nombre de particules du système, qu'on peut éventuellement faire varier ; La résultante de la transformation de Legendre par rapport à toutes les variables extensives naturelles V,S,N est la fonction grand potentiel définie par :

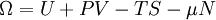
\Omega = U + PV - TS - \mu N~

où μ est le potentiel chimique de l'espèce considérée.

Les variables supplémentaires

On peut définir des enthalpies libres généralisées relatives aux propriétés électriques (ferroélectricité..), magnétiques(diamagnétisme, paramagnétisme, ferromagnétisme, ...) et des potentiels chimiques généralisés à plusieurs espèces chimiques différentes exactement de la même façon.

Cas du formalisme hamiltonien en mécanique classique

Le rapport entre le formalisme Lagrangien et le formalisme Hamiltonien en mécanique classique évoque de façon immédiate la transformée de Legendre. Partons du Lagrangien :

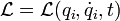
\mathcal{L}= \mathcal{L} ( q_i, \dot{q}_i, t)

qui est une fonction des coordonnées généralisées qi, des vitesses généralisées 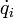\dot{q}_i et du temps t. Définissons pi, le moment généralisé associé à la coordonnée généralisée qi par: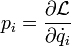

p_i = \frac{\partial \mathcal{L}}{\partial{\dot q_i}}

On définit alors la fonction de Hamiltonien 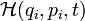\mathcal{H} (q_i, p_i, t) par :

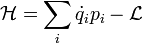
\mathcal{H} =\sum_i \dot{q}_i p_i - \mathcal{L}

qui est la transformation de Legendre du Lagrangien.

Annexes

Bibliographie

  • RKP Zia, Edward F Redish et Susan R Mckay, « Making Sense of the Legendre Transform » texte intégral
  • Portail de la physique Portail de la physique
Ce document provient de « Transformation de Legendre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformation de legendre de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Transformation de Legendre — La transformation de Legendre est une opération mathématique qui, schématiquement, transforme une fonction définie par sa valeur en un point en une fonction définie par sa tangente. Les cas classiques d utilisation de la transformation de… …   Wikipédia en Français

  • Legendre-Transformation — Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte hilf mit, die Mängel dieses… …   Deutsch Wikipedia

  • Legendre — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.  Pour l’article homophone, voir Gendre. Patronyme Legendre est un nom de famille notamment porté par : Antoine Legendre (1590 1665), botaniste… …   Wikipédia en Français

  • Legendre transformation — f(x) . The function is shown in red, and the tangent line at point (x 0, f(x 0)) is shown in blue. The tangent line intersects the vertical axis at (0, f^star) and f^star is the value of the Legendre transform f^star(p 0) , where p 0=dot{f}(x 0) …   Wikipedia

  • Legendre polynomials — Note: People sometimes refer to the more general associated Legendre polynomials as simply Legendre polynomials . In mathematics, Legendre functions are solutions to Legendre s differential equation::{d over dx} left [ (1 x^2) {d over dx} P n(x)… …   Wikipedia

  • Adrien-Marie Legendre — Pour les articles homonymes, voir Legendre. Adrien Marie Legendre Portrait charge de Adrien Marie Legendre[1] …   Wikipédia en Français

  • Associated Legendre function — Note: This article describes a very general class of functions. An important subclass of these functions mdash;those with integer ell and m mdash;are commonly called associated Legendre polynomials , even though they are not polynomials when m is …   Wikipedia

  • Canonical transformation — In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates (mathbf{q}, mathbf{p}, t) ightarrow (mathbf{Q}, mathbf{P}, t) that preserves the form of Hamilton s equations, although it might not preserve the… …   Wikipedia

  • Adrien Marie Legendre — [ləˈʒɑ̃ːdrə] (* 18. September 1752 in Paris; † 10. Januar 1833 ebenda) war ein französischer Mathematiker. Inhaltsverzeichnis 1 Leben 2 Werk 3 Sonstiges …   Deutsch Wikipedia

  • Adrien-Marie Legendre — Karikatur Legendres des französischen Künstlers Julien Leopold Boilly Adrien Marie Legendre [ləˈʒɑ̃ːdrə] (* 18. September 1752 in Paris; † 10. Januar 1833 ebenda) war ein französischer Mathematiker. Inhaltsverzeichnis …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”