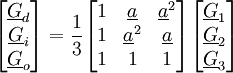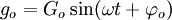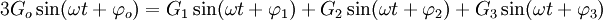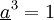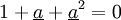Transformation de fortescue
- Transformation de fortescue
-
Transformation de Fortescue
Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) :
- Un système équilibré direct noté Gd.
- Un système équilibré inverse noté Gi.
- Un système de tension homopolaire noté Go (en réalité une grandeur monophasée que l'on divise en 3 pour le calcul matriciel).
Systèmes triphasés homopolaires
Comme expliqué précédemment, ce n'est pas vraiment un système triphasé car cela correspond à un système de 3 tensions en phase :
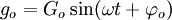
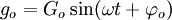
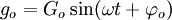
L'intérêt de ce faux système triphasé est de faciliter l'écriture matricielle de la transformation de Fortescue.
Matrice de transformation
Le but est de trouver les valeurs de Gd, Gi et Go à partir de G1, G2 et G3.
Calcul de Go
Comme la somme des trois grandeurs d'un système équilibré est nulle, on a forcément :
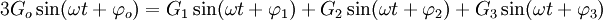
Opérateur de rotation : a
- Remarque : Une grandeur soulignée représente le nombre complexe associé à la grandeur sinusoïdale considérée.
C'est un nombre complexe de module 1 et d'argument 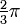 :
: 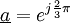
Le résultat de sa multiplication au nombre complexe associé à une grandeur correspond à une autre grandeur de même amplitude et déphasée de 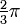 par rapport à la grandeur initiale. Il correspond à une rotation de
par rapport à la grandeur initiale. Il correspond à une rotation de 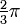 dans le plan de Fresnel.
dans le plan de Fresnel.
Il vérifie les propriétés suivantes :
Matrice de Fortescue inverse
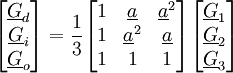
Voir aussi
Liens internes
Liens externes
 Portail de l’électricité et de l’électronique
Portail de l’électricité et de l’électronique
Catégorie : Électronique de puissance
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transformation de fortescue de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Transformation de Fortescue — Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) : un système équilibré direct noté Gd ; un système équilibré inverse noté Gi ; un système de… … Wikipédia en Français
Fortescue — Transformation de Fortescue Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) : Un système équilibré direct noté Gd. Un système équilibré inverse noté Gi … Wikipédia en Français
Transformation des systemes triphases — Transformation des systèmes triphasés Les transformations des systèmes triphasés sont utilisées dans l étude des machines électriques. Ces transformations permettent : d établir le schéma monophasé équivalent d une machine électrique… … Wikipédia en Français
Transformation des systèmes triphasés — Les transformations des systèmes triphasés sont utilisées dans l étude des machines électriques. Ces transformations permettent : d établir le schéma monophasé équivalent d une machine électrique triphasée ; de faciliter la commande des … Wikipédia en Français
Transformation clarke — Transformée de Clarke La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé Un système triphasé constitué de bobines et de courants déphasés entre eux de… … Wikipédia en Français
Transformation de Clarke — Transformée de Clarke La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé Un système triphasé constitué de bobines et de courants déphasés entre eux de… … Wikipédia en Français
Composant symétrique — Transformation de Fortescue Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) : Un système équilibré direct noté Gd. Un système équilibré inverse noté Gi … Wikipédia en Français
Composante homopolaire — Triphasé Graphique des trois tensions de même fréquence/amplitude et déphasées de 120° Le triphasé est un système de trois tensions sinusoïdales de même fréquence et généralement de même amplitude qui sont déphasées entre elles (de 120 ° ou… … Wikipédia en Français
Composantes symétriques — Triphasé Graphique des trois tensions de même fréquence/amplitude et déphasées de 120° Le triphasé est un système de trois tensions sinusoïdales de même fréquence et généralement de même amplitude qui sont déphasées entre elles (de 120 ° ou… … Wikipédia en Français
Courant triphasé — Graphique des trois tensions de même fréquence/amplitude et déphasées de 120° Un système de courant (ou tension) triphasé est constituée de trois courants (ou tensions) sinusoïdaux de même fréquence de même amplitude qui sont déphasés entre eux… … Wikipédia en Français
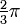 :
: 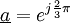
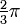 par rapport à la grandeur initiale. Il correspond à une rotation de
par rapport à la grandeur initiale. Il correspond à une rotation de 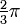 dans le plan de Fresnel.
dans le plan de Fresnel.