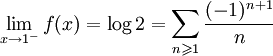Theoreme d'Abel (analyse)
- Theoreme d'Abel (analyse)
-
Théorème d'Abel (analyse)
Le théorème d'Abel, ou théorème de convergence radiale d'Abel, est un outil central de l'étude des séries entières.
Démonstration
Quitte à effectuer un changement de variables linéaire u = x / R, on peut considérer uniquement le cas R = 1.
La démonstration repose sur la méthode classique de la transformation d'Abel, équivalente à l'intégration par parties pour les intégrales. Notons Sn les sommes partielles de la série 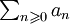 (avec la convention S − 1 = 0) et l sa somme, alors :
(avec la convention S − 1 = 0) et l sa somme, alors :
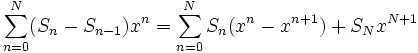
Pour tout x < 1, on a donc prouvé que 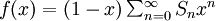 . Prenons N0 tel que | Sn − l | < ε pour tout
. Prenons N0 tel que | Sn − l | < ε pour tout 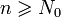 , alors pour 0 < x < 1:
, alors pour 0 < x < 1:
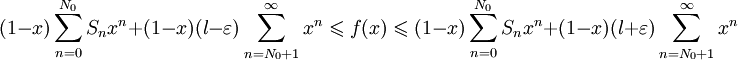
Comme d'une part la suite Sn est bornée car convergente, et d'autre part 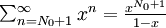 , on obtient :
, on obtient :
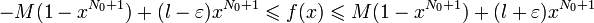
Les membres de gauche et de droite tendent respectivement vers l − ε et l + ε quand x tend vers 1.
Remarque : dans le cas où la série 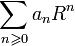 est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.
est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.
En effet, sous cette condition, 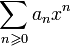 converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :
converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :
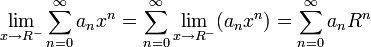
Exemple (2) :
Soit
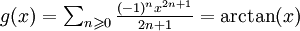
. Encore par le critère de convergence des séries alternées, on peut affirmer que
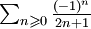
converge, d'où :
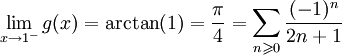
 Portail des mathématiques
Portail des mathématiques
Catégories : Série | Théorème d'analyse
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme d'Abel (analyse) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème d'Abel (Analyse) — Pour les articles homonymes, voir Théorème d Abel. Le théorème d Abel, ou théorème de convergence radiale d Abel, est un outil central de l étude des séries entières. Théorème Soit … Wikipédia en Français
Théorème d'abel (analyse) — Pour les articles homonymes, voir Théorème d Abel. Le théorème d Abel, ou théorème de convergence radiale d Abel, est un outil central de l étude des séries entières. Théorème Soit … Wikipédia en Français
Théorème d'Abel (analyse) — Pour les articles homonymes, voir Théorème d Abel. Le théorème d Abel, ou théorème de convergence radiale d Abel, nommé d après Niels Henrik Abel, est un outil central de l étude des séries entières. Sommaire 1 Énoncé 2 … Wikipédia en Français
Theoreme fondamental de la theorie de Galois — Théorème fondamental de la théorie de Galois En mathématiques et plus précisément en algèbre, le théorème fondamental de la théorie de Galois établit une correspondance entre la structure de corps et le groupe de Galois. Ce théorème permet l… … Wikipédia en Français
Théorème fondamental de la théorie de galois — En mathématiques et plus précisément en algèbre, le théorème fondamental de la théorie de Galois établit une correspondance entre la structure de corps et le groupe de Galois. Ce théorème permet l analyse de la structure de corps d une bonne… … Wikipédia en Français
ABEL (N. H.) — À l’aube du XIXe siècle, le mathématicien norvégien N. H. Abel allait révolutionner sa science, et Hermite a pu déclarer: «Il a laissé aux mathématiciens de quoi s’occuper pendant cinq cents ans.» D’abord algébriste, il établit l’impossibilité de … Encyclopédie Universelle
Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de Picard-Lindelöf — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de cauchy-lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de Cauchy-Lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. En mathématiques, et plus précisément en a … Wikipédia en Français
 Pour les articles homonymes, voir Théorème d'Abel.
Pour les articles homonymes, voir Théorème d'Abel.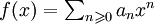 une série entière de rayon de convergence égal à R. Si
une série entière de rayon de convergence égal à R. Si 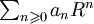 converge, alors :
converge, alors :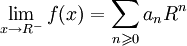 .Démonstration
.Démonstration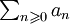 (avec la convention S − 1 = 0) et l sa somme, alors :
(avec la convention S − 1 = 0) et l sa somme, alors :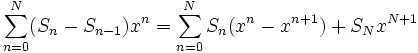
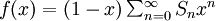 . Prenons N0 tel que | Sn − l | < ε pour tout
. Prenons N0 tel que | Sn − l | < ε pour tout 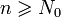 , alors pour 0 < x < 1:
, alors pour 0 < x < 1: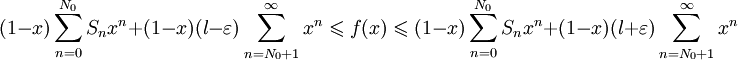
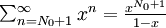 , on obtient :
, on obtient :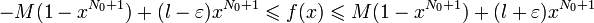
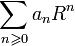 est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.
est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.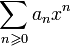 converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :
converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :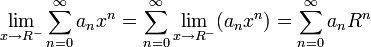 Exemple (1) :Exemple (2) :Soit
Exemple (1) :Exemple (2) :Soit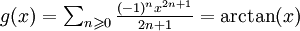 . Encore par le critère de convergence des séries alternées, on peut affirmer que
. Encore par le critère de convergence des séries alternées, on peut affirmer que 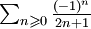 converge, d'où :
converge, d'où :
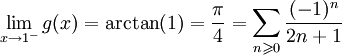

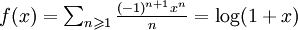 . Comme
. Comme 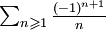 converge (d'après le
converge (d'après le